- Find <x>, <x2>,
<p>
<p2> for the nth
eigenfunction. Use the results to find the uncertainity in
x, and p and the product of the two.
Compare to Heisenberg's result.
- Consider a wavefunction that at t=0 is the sum of the first
two eigenfunctions:
 = N( | 1 > + | 2 > )
= N( | 1 > + | 2 > )
Write down the wavefunction as a function of time. Plot the
position probability density for several times (maybe make a movie
of how it changes in time). Calculate <x>
and <p> as functions of time, and check that
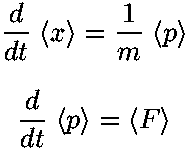
is true.
- Consider the t=0 wavefunction:
 = Nx(1 - x )
= Nx(1 - x )
Normalize this wavefunction and expand it in infinite-square-well
eigenfunctions. Since you can't find all  expansion coefficients, do what you think is "enough" and justify
your choice of where to stop.
expansion coefficients, do what you think is "enough" and justify
your choice of where to stop.
- On page 3 I noted how in
the quantum fall energy spacing decreased with increasing energy, whereas
in the square well energy spacing increased with increasing energy and stated
that the WKB approximation provided an answer. Starting with the
usual WKB approximation:
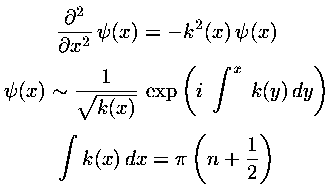
show that the energy spacing is determined by the classical period
(T):

Find T(E) classically for the square-well,
harmonic oscillator, and quantum fall and check the above relationship.
- Following the methods of page 4
find the eigenenergies and eigenfunctions for U0'=50.
According to the plot of k' vs 1/U0'
you should find 3 bound states. Using your eigenfunctions check the
orthogonality between the ground state and the highest energy bound state.
Find the probability of finding the highest energy bound state particle
in the classically disallowed region.
- A particle sits in the ground state of an infinite (1d) square well.
At t=0 the infinite square well is reduced to one with
U0'=50. Find the probability that the
particle ends up in an unbound state.
- On page 5 I claim that if:
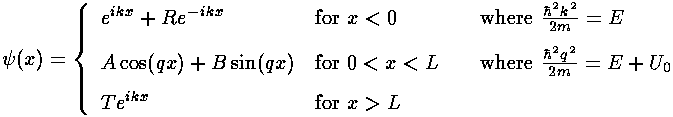
then:
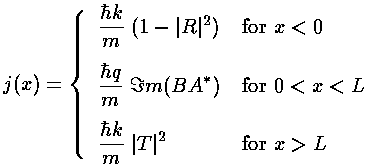
Verify this result.
- On page 5 I note:
Note the zero reflection when
qL=n , i.e., when the infinite
square well version of the finite well has a bound state at the energy
of the incoming particles. Experimentally one might hope to see oscillations
in reflectivity just by raising the beam's energy. From the second plot see
that it is difficult to get more than one good oscillation just by
raising the beam energy.
, i.e., when the infinite
square well version of the finite well has a bound state at the energy
of the incoming particles. Experimentally one might hope to see oscillations
in reflectivity just by raising the beam's energy. From the second plot see
that it is difficult to get more than one good oscillation just by
raising the beam energy.
How does the wavefunction in the finite square well for qL=n compare to the wavefunction for an infinite squre well bound state
at the same energy?
compare to the wavefunction for an infinite squre well bound state
at the same energy?
Pick various values of U0' and plot |R|2
vs E'. Find a value of U0' in which the
oscillations are as "nice" as possible.
- On page 7 we discuss the bound states
of a 2d rectangular infinite square well. The following diagram is
the result:
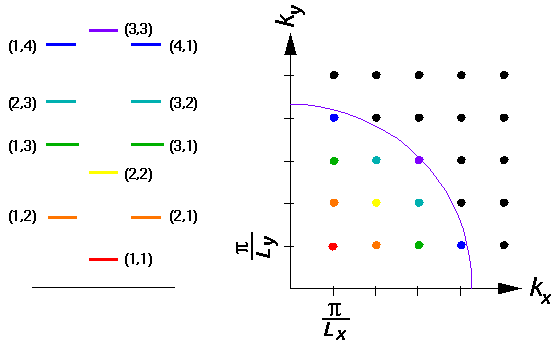
The purpose of such a diagram is to display a method for finding
an approximate count of the
total number of states with energy less than some particular
E'=k'2. [Such a count is needed to solve many
problems in thermodynamics.] Notice that each state is represented as
a dot in the upper right hand corner of a small rectangle with
sides  /Lx and
/Lx and
 /Ly. Such rectangles nearly
fill-out the 1/4 circle with radius k and thus the number
of such rectangles can be approximated from the area of the 1/4
circle and the area of one rectangle. [The result is clearly an
over estimate for the number of states because, for example, the
(2,4) state has less energy than is shown by the purple arc, but much of
its area is needed to fill-out the 1/4 circle. The over-counting
is usually an insignificant fraction for large enough k'.]
Find the approximate number of states with energy less than
E'
/Ly. Such rectangles nearly
fill-out the 1/4 circle with radius k and thus the number
of such rectangles can be approximated from the area of the 1/4
circle and the area of one rectangle. [The result is clearly an
over estimate for the number of states because, for example, the
(2,4) state has less energy than is shown by the purple arc, but much of
its area is needed to fill-out the 1/4 circle. The over-counting
is usually an insignificant fraction for large enough k'.]
Find the approximate number of states with energy less than
E'
In a similar way we displayed on page 13
the energy levels in 3d:

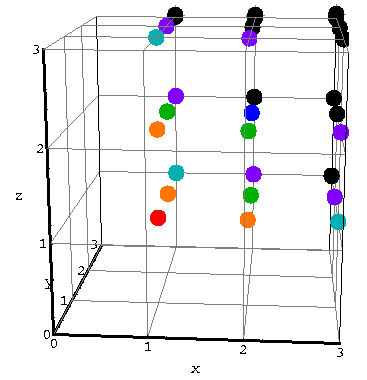
Use a similar approach to find the approximate number of states
in 3d with energy less than E'.
- The previous question suggests that some thermodynamical
properties (e.g., the pressure of an ideal (non-interacting) gas confined to
a box) depend on the number of states with energy less than a given
value. However the number of such states would seem to depend on
the fine details of the potentials, whereas, for example, the pressure of a gas depends
only on the volume and not the shape of the volume. Thus I claim that for large
E' the number of states per area (2d), or volume (3d) in fact doesn't
depend on the shape of the potential. The below table presents the number
of states with energy less than E' is a (2d) round infinite square-well.
| E' | # of states with
energy < E'
|
|---|
| 30 | 5
|
| 100 | 21
|
| 300 | 67
|
| 1000 | 232
|
| 3000 | 725
|
On page 8 a display shows the energy levels
with E'<80. Check to see that there are 5 levels with
E'<30; what (undisplayed) levels have energy 80<E'<100.
to give a count of 21 levels with energy below 100.
Compare the number of states per area of the [round] potential to that
calculated in the above problem.
Calculate the number of states with energy less than E' for several
values of E' in a spherical square-well and compare
to that calculated in the above problem.
- A picture on page 8 purports to show
a classical motion with: L'=10 and E'=1037.6. In fact
the picture is distorted. Draw an accurate classical trajectory with
those parameters. See if you can find any other "interesting" trajectories.
- Find the eigenenergies and wavefunctions for U0'=25.
Make a stacked wavefunction plot like that on page 9.
- Look up Brewster's angle in your E&M or optics book
in order to find equations describing the reflect/refraction of light
(sometimes called Fresnel formulas). Read those sections and summarize
the relevant results/formulas.
Does QM have someting like
Brewster's angle? Why or why not. In what sense is QM scattering like
light scattering? How does QM total internal reflection compare to light
total internal reflection. Find an explanation for evanescent wave
[e.g., Barger & Olsson p.397] and compare it to QM tunneling.
- Pick some value of
the recursion relation for U0' and E' (i.e., for
n) and plot the reflection probability vs. angle of incidence.
- Consider a 1d step...find appropriate (propagating) wavefunctions
on either side of the step, and use appropriate boundary conditions to
connect the solutions.
Explicitly report the probability flux in (1) the incident wave, (2) the
reflected wave and (3) the transmitted wave [careful].
Find the reflection and transmission probabilites.
- Derive the formula:

- Following the methods of page 11
plot the differential cross-section at k'=5.
Which phase shifts deviate more than .01 r from 0?
- Following the methods of page 12
find the low energy cross-section for U0=49.
How/why does it differ from that for U0=50
described on the hrefed page?
- Following the methods of page 12
find plot cross-section for U0=25 out to
k'=5. Find an example of a resonance and provide evidence
that it is a resonance.
- Look for N=2 rainbows in the range of parameters
of the previous problem. Provide a plot of
 2
vs b showing a rainbow. Plot |f|2 at
the rainbow and show where it should be.
2
vs b showing a rainbow. Plot |f|2 at
the rainbow and show where it should be.
- Consider a box where Lx=Ly=L
but Lz varies. Find the l0 lowest eigenenergies in the
limits Lz>>L and Lz<<L.
Sketch how the lowest 10 eigenenergies vary for Lz near L.
- Consider an infinite 3d square-well with an allowed region like
the inside of a (finite height) cylinder. Solve the Schrödinger's equation
in cylinderical coordinates. Consider the limits Lz>>R
and Lz<<R. If possible compare to the results
of the previous problem. What value of Lz produces
3 degenerate states for the first excited states [as seen in the cube and
sphere]?
- Electrons moving inside a cylinder as in the previous problem
may be considered a crude model for the bonding electrons in a homonuclear
diatomic molecule like O2 or N2. Consider a cylinder with
radius a=1Å and height Lz=2.8Å to
be filled [aufbau] with some electrons. Find the ten low energy eigenenergies
(in eV) and display
the results in a level diagram. Label each state as to nz,
nr, and m. m values are to be disguised
in greek symbols: m=0 is
 , m=±1
is
, m=±1
is  , m=±2 is
, m=±2 is  (think: spd..., just like angular momentum l=0,1,2...). If you symmetrically
place the origin at the center of mass of the cylinder, the states have
definite symmetry wrt "inversion" i.e.,
(think: spd..., just like angular momentum l=0,1,2...). If you symmetrically
place the origin at the center of mass of the cylinder, the states have
definite symmetry wrt "inversion" i.e.,
z -z
-z
r r
r


 -
-
As you can see, inversion in vector form is:
r -r
-r
states that are "even" under inversion are to be labeled "g" [for German: gerade],
states that are "odd" under inversion are to be labeled "u" [for German: ungerade].
States that have odd z-parity and hence have a nodal plane through
the center of mass of the cylinder are called antibonding; states that have even parity
and hence have an antinode at the center of mass of the cylinder are called bonding.
Label each of your anitbonding states with a "*" superscript.
Repeat the process for Lz=3.0Å. What has changed?
- Consider the series: Li2, Be2, B2,
C2, N2, O2, F2 in which we have
a total of 2, 4, 6, 8, 10, 12, 14 non-core (bonding) electrons. "Aufbau"
these molecules using your above energy level diagram (with Lz=2.8Å).
A crude estimate of the "bond order" is the number of pairs of electrons in
bonding orbitals minus the number of pairs of electrons in antibonding orbitals.
Calculate the bond order and display each diatomic molecule as having
a single bond, double bond, etc. (Here is a brief
review of chemical bonding.). The below table lists the bond strength (essentially
the energy needed to disassociate the molecule) in eV.
| Molecule | Bond Strength
(eV)
|
|---|
| Li2 | 1.1
|
| Be2 | 0.6
|
| B2 | 3.1
|
| C2 | 6.3
|
| N2 | 9.8
|
| O2 | 5.2
|
| F2 | 1.6
|
Do a linear least square fit to bond strength as a function of bond order.
Is it a "good" fit? [Defend your answer!] What
is the estimated bond strenth per bond? Try fitting two other functional forms.
Are the results better than linear? [Defend your answer!] "Aufbau" again using
the Lz=3.0Å level diagram. How does the linear fit
work now? Can you think of any other ways of distinguishing experimentally between the
predictions of the two energy level diagrams?
- The deuteron (D) is a bound state of neutron and proton in the nuclear potential,
which we model as a 3d finite square well.
Using relative coordinates we have a particle with a (reduced) mass of mp/2
in a potential with unknown range a and depth U0.
Experimentally we know that the bound state energy E is just 2.225 MeV
less than the top of the well (i.e., a binding energy of 2.225 MeV), and thus there are
no other bound states other than this s state. The mean-square radius of
the deuteron wavefunction has been measured to be:
<r2> = (4.2 fm)2
Use these two bits of data to find a and U0.
- The the consituents of a nucleus (neutrons and protons) are often described
as moving in a nuclear potential that is approximately like a finite square well.
Since the neutron and proton are different fermions, the set of neutron energy levels
are filled up [following Pauli exclusion] quite distinctly from the proton energy
levels, even though both particles feel much the same potential.
The actual order of filling in nuclei [for both neutrons and protons] seems to be:
1s, 1p, 1d,
2s, 1f, 2p, 1g... How does this order compare
to that in the infinite square well? Write down the orbitals occupied by helium's
two neutrons and two protons: 4He; oxygen: 16O; tritium: 3H,
helium-3: 3He. For each of the above seven listed states find the value of
U0'
at which the state just barely exists. Assume for the moment that the depth of the potential
U0 is constant, so varying U0' are to be interpreted
as varying a. Now plot a (in some sense the size of the nucleus)
[or rather [U0']½ which would be proportional a]
on the y axis vs. the number of nucleons that well can hold (A).
Try to fit some functional form to the resulting plot. [PS...there is actually a bit of
Nobel-prize winning physics that must be added to this very naive picture of the nucleus:
spin-orbit coupling.]
- Consider bottomium (a b anti-b quarkonium particle).
The ratio of the (3s-2s) energy difference over
the (2s-1s) energy difference for the bottomonium system is
(10.3553-10.0233)/(10.0233-9.460)=.59. [1s means the l=0 ground state.]
Find a 3d finite square well U0'
that matches this ratio. What other bound states exist for this potential?
Experimentally one finds the ratio of the (1p-1s) energy difference over
the (2s-1s) energy difference for the bottomonium system is
(9.9-9.460)/(10.0233-9.460)=.78. What do you get for your square well?
 = N( | 1 > + | 2 > )
= N( | 1 > + | 2 > )
 = Nx(1 - x )
= Nx(1 - x )
 expansion coefficients, do what you think is "enough" and justify
your choice of where to stop.
expansion coefficients, do what you think is "enough" and justify
your choice of where to stop.
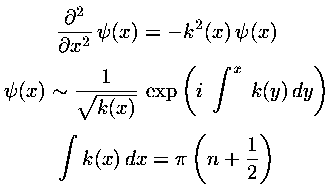

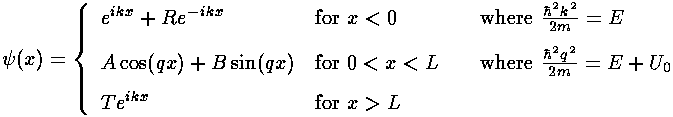
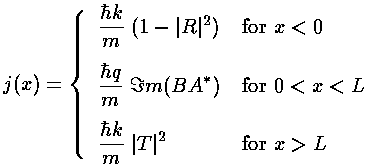
, i.e., when the infinite square well version of the finite well has a bound state at the energy of the incoming particles. Experimentally one might hope to see oscillations in reflectivity just by raising the beam's energy. From the second plot see that it is difficult to get more than one good oscillation just by raising the beam energy.
 compare to the wavefunction for an infinite squre well bound state
at the same energy?
compare to the wavefunction for an infinite squre well bound state
at the same energy?

 /Lx and
/Lx and
 /Ly. Such rectangles nearly
fill-out the 1/4 circle with radius k and thus the number
of such rectangles can be approximated from the area of the 1/4
circle and the area of one rectangle. [The result is clearly an
over estimate for the number of states because, for example, the
(2,4) state has less energy than is shown by the purple arc, but much of
its area is needed to fill-out the 1/4 circle. The over-counting
is usually an insignificant fraction for large enough k'.]
Find the approximate number of states with energy less than
E'
/Ly. Such rectangles nearly
fill-out the 1/4 circle with radius k and thus the number
of such rectangles can be approximated from the area of the 1/4
circle and the area of one rectangle. [The result is clearly an
over estimate for the number of states because, for example, the
(2,4) state has less energy than is shown by the purple arc, but much of
its area is needed to fill-out the 1/4 circle. The over-counting
is usually an insignificant fraction for large enough k'.]
Find the approximate number of states with energy less than
E'



 2
vs b showing a rainbow. Plot |f|2 at
the rainbow and show where it should be.
2
vs b showing a rainbow. Plot |f|2 at
the rainbow and show where it should be.
 , m=±1
is
, m=±1
is  , m=±2 is
, m=±2 is  (think: spd..., just like angular momentum l=0,1,2...). If you symmetrically
place the origin at the center of mass of the cylinder, the states have
definite symmetry wrt "inversion" i.e.,
(think: spd..., just like angular momentum l=0,1,2...). If you symmetrically
place the origin at the center of mass of the cylinder, the states have
definite symmetry wrt "inversion" i.e.,
 -z
-z
 r
r


 -
-
 -r
-r