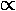± K|m|(
r)
exp(im
) where:
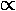± K|m|(r)
exp(im) where:
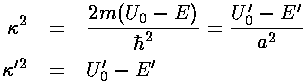
because Km is the normalizable (decreasing exponential) solution to Schrödinger's equation there. Inside of the well (i.e., r<a) we must have
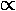J|m|(kr)
exp(im) where:
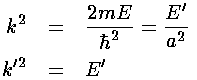
because Jm is the normalizable (regular at zero) solution to
Schrödinger's equation there. These two solutions need to match up
at the well boundary; we require both and
to be continuous at r=a.
(The second derivative of
will have a step at r=a to match the step in potential as
required by Schrödinger's equation.) As before dividing the
-match equation by the -match equation
(i.e., matching the logarithmic derivative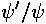 
) eliminates
the unknown normalization constants:
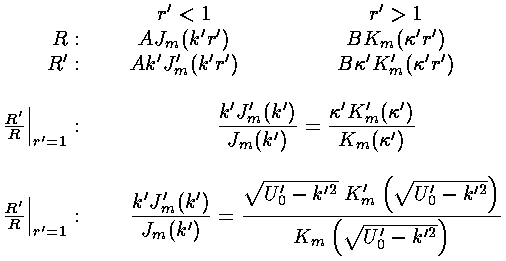
The 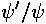equation is a nonlinear equation
for the unknown k' given the size of the potential step: U0'.
Clearly 0<k'<(U0')½.
We examine the nature of the solutions by displaying the right hand side of the
equation in blue and the left hand side in red. Solutions are where the two curves
cross.
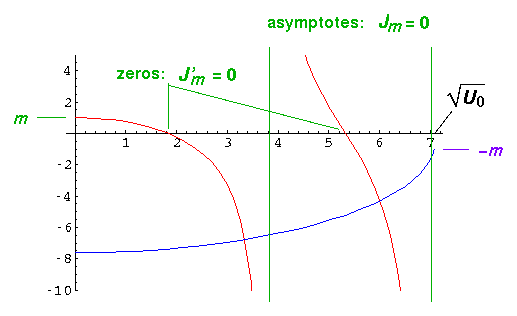
The lhs (red) starts (k'=0) with y value m; it crosses
the x-axis at the zeros of Jm' and reaches
±
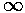asymptotically at the zeros of Jm.
The rhs (blue) is always negative since the Km(x) have negative
slope; in fact, since for large x
Km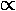(x) e-x
so Km'/Km should be approximately -1. Thus the rhs should start at nearly -(U0')½. It ends at k'=(U0')½ with a y value of -m. [The above plot is for m=1 and U0'=50 and shows two solutions. The wavefunctions are displayed below.] Clearly there will typically be an intersection for k' between a zero of Jm' and a zero of Jm. Since J0' has a zero at k'=0, there is always a solution for m=0, even for arbitrarily small potentials. For m=1 a solution requires U0'>5.78; m=2, U0'>14.7.
Once the magic value of k' is found, the following wavefunction
has continuous and .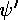
The constant A is determined by normalizing the wavefunction.
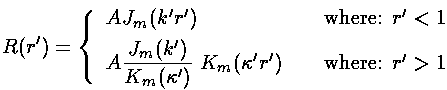
Here are some resulting wavefunction for U0'=50.
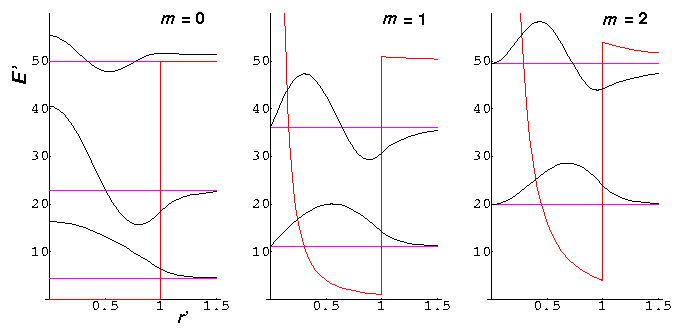
Note that the m=0 nr=2 wavefunction is
just barely bound: E'=49.992. Since the region r'>1
is just barely disallowed, the wavefunction extends deeply into the
large r' region, and hence the probability of finding the particle
in the allowed region is unusually small (i.e.,
is relatively small for this wavefunction in the allowed region).
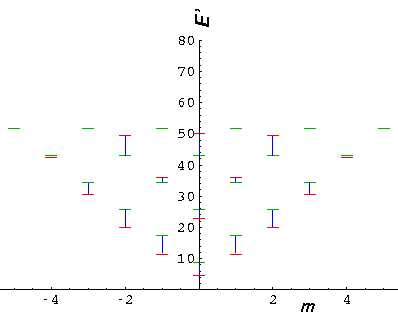
Below is a plot comparing the infinite square well energies with those of the U0'=50 system (each infinite square well energy [in black] is connected by a blue line to the equivalent finite square well energy [in red]).
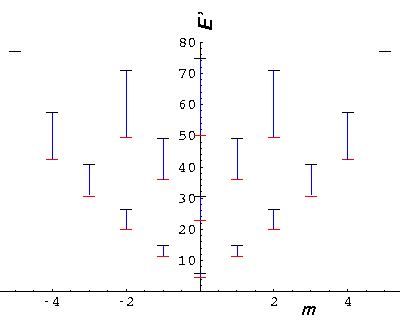
It is also interesting to compare our U0'=50 system to a simple harmonic oscillator system (seen below in green). The shm system has an exact m degeneracy crudely reflected in the U0'=50 system where the high |m| states are lower than the "equivalent" low |m| states. While the energy spacing is exactly constant in the shm system, the U0'=50 system spacings are increasing (but not as much as the infinite square well).
