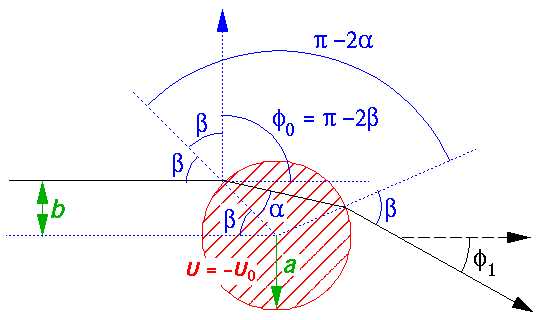
We have already studied the bound states in such a potential. We then used a shifted energy origin so that the potential was zero at the bottom of the well. Here we take the the top fo the well to be U=0. This is the same strategy we adopted in 1d when we studied bound states in finite square wells and then scattering from finite square wells.
As we have seen, classically
the effect of entering a region with U=-U0
is much like refraction. The component of velocity parallel to the
interface's normal is increased (as required by conservation of energy) while
the component of velocity parallel to the interface is
unchanged (as there is no force in that direction). The angle of
incidence (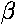
) and the angle of refraction
(
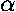) end up related as in Snell's Law:
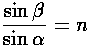
We seek to relate the impact parameter (b) to the
scattering ange (
). Remember that on the
previous page we found the relationship between the
counter-clockwise reflection
angle (here called 0) and the
impact parameter. The effect of refraction is identical to that
of reflection except the normal of the exit point has been
rotated clockwise by the angle:
-2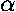
Thus the result of refraction is our previous result minus (because it's clockwise) the rotation of the normals.
While classically (and even in the WKB approximation) there is no reflection, we know from our previous work that reflection will accompany refraction in quantum mechanics. Thus we can have immediate reflection or we can have one or more reflections inside the potential well. That is to say the path of the "particle" may include N=0,1,2,... internal chords. The net result of an N internal chords, is to rotate the exit normal from the entrance normal by:
N(-2)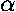
Thus, we have the relationship between the scattering angle and the impact parameter:
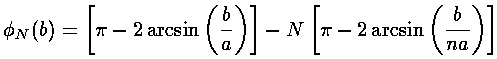
We plot some of these results in the case n=1.33 (which happens to be the refractive index for visible light in water).
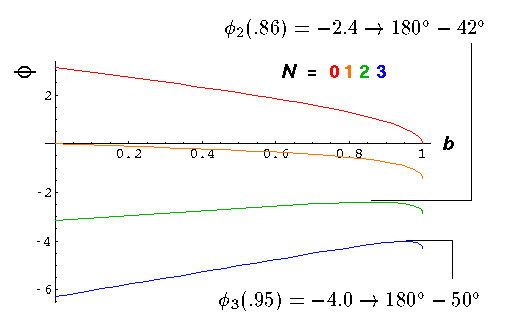
Note in particular the curves for N=2, (and 3).
We see that the scattering angle has a minimum (maximum)
at an angle equivalent to =2.40
(2.27). (N=2 scatters light in the range:
[138°, 180°], N=3 scatters light in the range:
[0, 130°]. Between the bows we have Alexander's dark band.)
Since the angle is extremal, the derivate of
with respect to b will be zero there, and hence the
differential cross-section will be infinite at that point since:
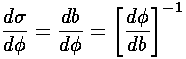
What's happening is that particles from a fair range of b
near the extremal, end up scattering to pretty much the same
degree. So particles from a "finite" range of b are being
concentrated into an "infinitesimal" range of ,
and the result is an infinite cross-section. This is called
a rainbow. [It explains why a rainbow is bright; rainbows
are colored because n depends on the the light's color, so
the different colors of light end up having slightly different
rainbow angles.] For water we see that there is a rainbow
(the "primary" rainbow) from scattering
with two internal chords: 42° from the anti-solar point
[i.e., nearly backscattered off the raindrops].
Scattering with three internal chords produces a rainbow
(the "secondary" bow, often
not seen and always dimmer than the primary bow---it also has its
colors reversed from the primary bow) 50° from the anti-solar point
(i.e., beyond the primary bow). The below shows the extremal paths of the
rays for N=2,3.
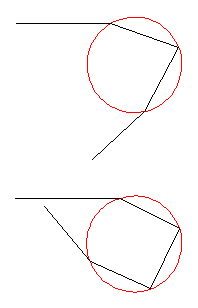
We can cobble together a "classical" cross-section by taking our previous result for the probability of reflection, and apply it every time the particle touches the interface. Here is the result for n=1.33:
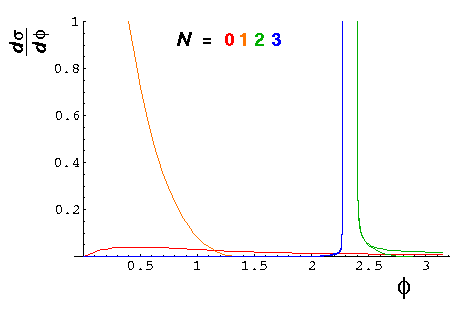
Note that most of the scattering comes from N=1, i.e., pure refraction. Nevertheless the infinite cross-sections due to the rainbows for N=2,3 are quite visible. Here is a blow-up of the rainbow region:
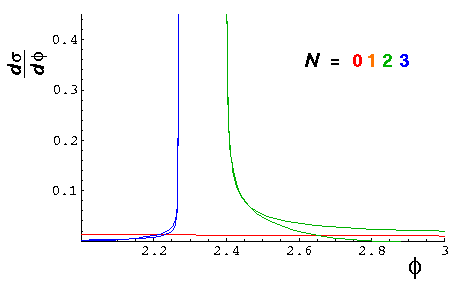
Note (most noticable from the green N=2 curve) that the "rainbow" has a "double valued function"...two different rays end up at the same angle. In classical mechanics we would just add these scattering probabilities. In wave mechanics, different paths means different phases...we should expect interference in the rainbow region between the rays that have taken different paths to get to the same scattering angle.
In making the connection between particles and QM, note that
n is a strong function of energy. Thus at low energy
n is large and reflection becomes quite likely; whereas at high energy
n
1 and the cross-section declines.
In quantum mechanics we proceed much as on the previous page. Outside the well we have solutions of the form:
Jm(k'r') cos(m) and
Ym(k'r') cos(m)
where E'=k'2. We choose to write our solution a as sum of Hankel functions:
[Hm(2)(k'r') +
exp(2i
m)
Hm(1)(k'r') ] cos(m)
Inside the well the solution must be regular at the origin and hence a J:
Jm(q'r') cos(m)
where E'+U0'=q'2 (i.e., the particle has more momentum when inside the well).
Our job is to match the logarithmic derivative
(
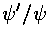) at the well boundary (r'=1). Thus:
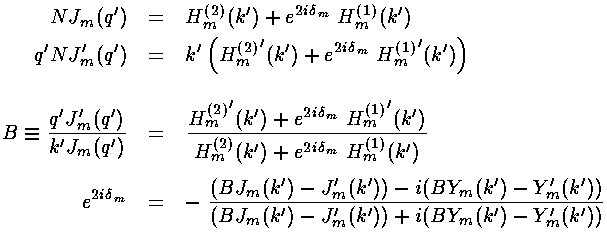
Consider the previously worked case of U0'=50. Recall that we had three bound states for m=0, two bound states for m=1,2, one bound state for m=3,4, and no other bound states for larger m. The highest energy m=0 bound state was extremely weakly bound. We plot below the phase shifts (m=0-5) for this problem as function of particle momentum k':
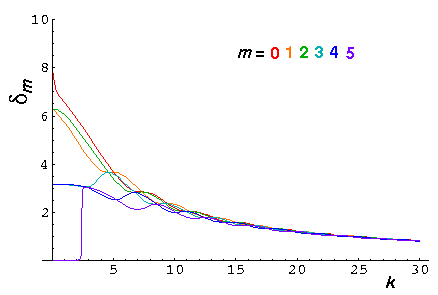
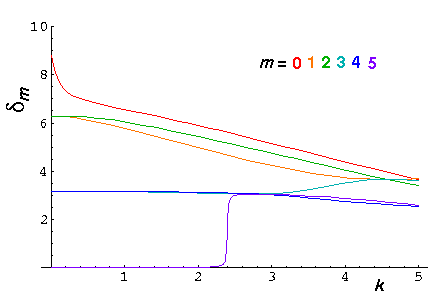
The phase shifts are positive for this attractive potential whereas they were negative for the reflecting (repulsive) potential.
Note that at high energy, all phase shifts approach the same value, which as given in the WKB approximation is:
=½U0'/k'
Note that at low energy, all the phase shifts (seemely except
m=0 which we address below), approach a multiple of
, which means the same as =0:
no scattering. If |B| is large (as it usually is at low energy
[small k']) the above phase-shift formula reduces to the phase shift formula for
the fully reflective well. Thus, exactly as on the previous page,
we expect the mth phase shift to go to "0" like
k'2m. The k'=0 value of
the phase shift is j, where
j is the number of bound states with that value
of m. (The highest energy bound state has "sucked in"
j of phase [e.g., it has
j-1 nodes]. Higher energy states [e.g., E=0]
start with this phase which is reduced at high energy
(where n1) to zero.)
The m=0 state is different in this case because there is a very weakly bound state an thus J'm(q') is quite small and hence one must go to extremely low values of k' before |B| become large. A non "0" phase shift means significant scattering. The below plots of differential cross-sections show larger, low energy s scattering than we saw in the fully reflective case.
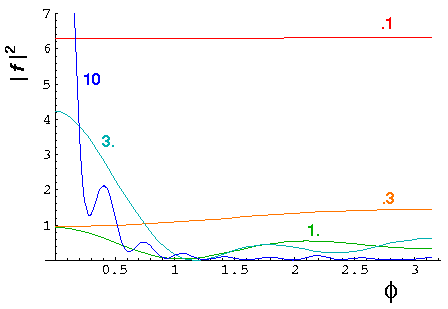
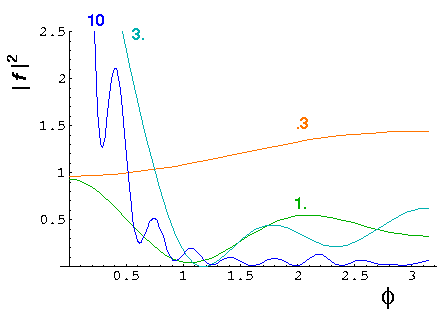
It is helpful to define the total cross-section:
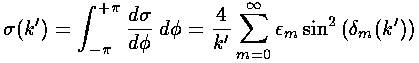
The total cross-section is related to the fraction of the particles experiencing any scattering in the sample. We plot below the total cross-section as a function of k'
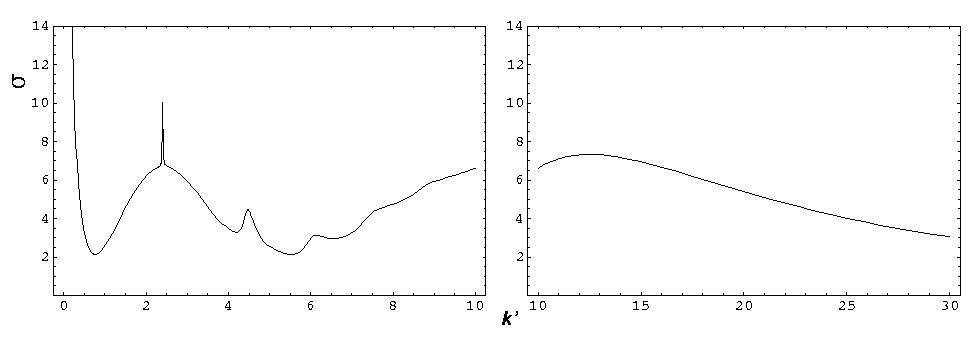
(Note the scale change in the "dull" region: k'>10.) Note the sharp peak (resonance) near k'=2.4 (and weaker peaks at 4.5, 6, ...). Notice that the m=5 phase shift reaches maximum scattering (90°) near k'=2.4. Consider three differenctial cross-section plots at k'=2.3 (red), 2.4 (green), and 2.5 (blue).
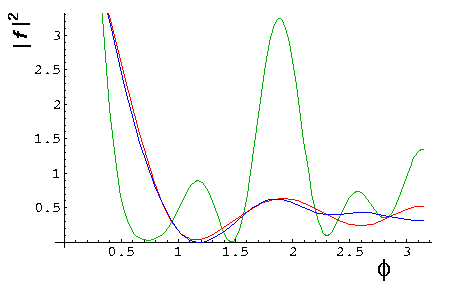
Notice that the "resonant" k'=2.4 cross-section is
much different from the others. If we display the m=5
wavefunction [cos(5)]2, I can
maybe convince you that the difference is due to the appearance
and then disappearance of the m=5 wavefunction.
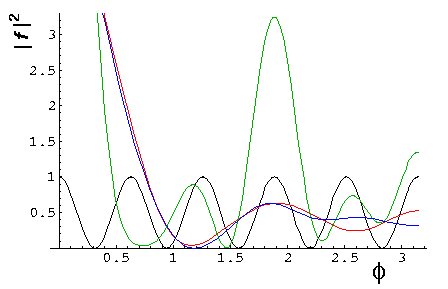
The below is a plot of the solution to Schrödinger's equation for k'=2.4 m=5.
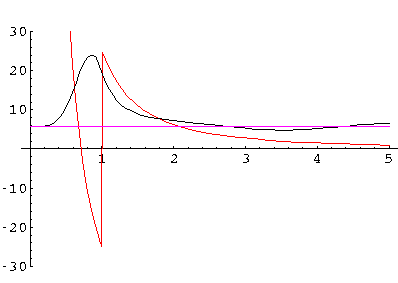
Note that there is a perfectly good classically allowed region between r'=0.7 and 1.0 which is connected through a disallowed region between 1 and 2.1 to the large r' allowed region. Tunneling should come to mind... Classically we can have a particle bound between 0.7 and 1, but tunneling allows the probability to escape. To have a standing wave solution to Schrödinger's equation we need to feed a little flux into the well to make up for what tunnels out. The oscillation in the large r' allowed region is the incoming and outgoing flux from/to what is nearly a bound state. If we shift the energy slightly the near bound state condition disappears. Our Schrödinger's equation solution (10x) now looks like:
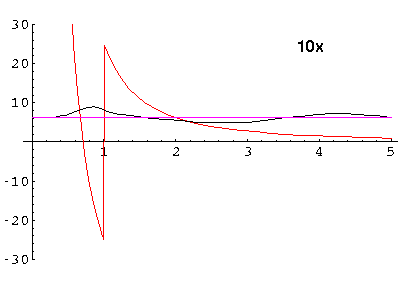
Note particularly the inside/outside ratio is now much reduced.
There is nothing special about m=5; there are other resonances for larger m [i.e., (m,k')=(6,4.5), (7,6), ...]. The "sharpness" of the resonance [i.e., the small range of energy in which it is obvious] is degraded by reducing the size of the disallowed region, which happens at higher energy. Thus m=5 is the first and hence sharpest of these resonances.
Here are solme plots of the probability density for our U0'=50 potential. First at k'=1 with a blow-up of the central region.
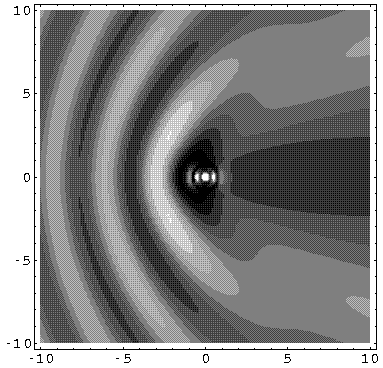
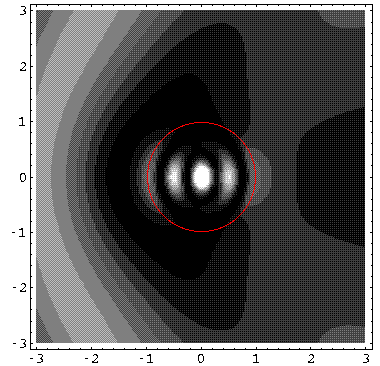
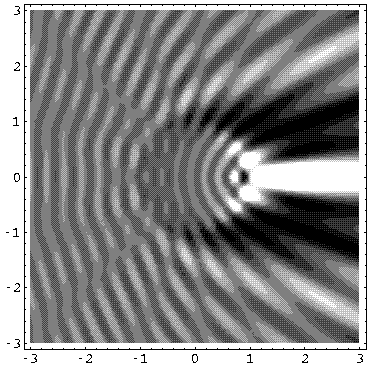
followed by k'=10.
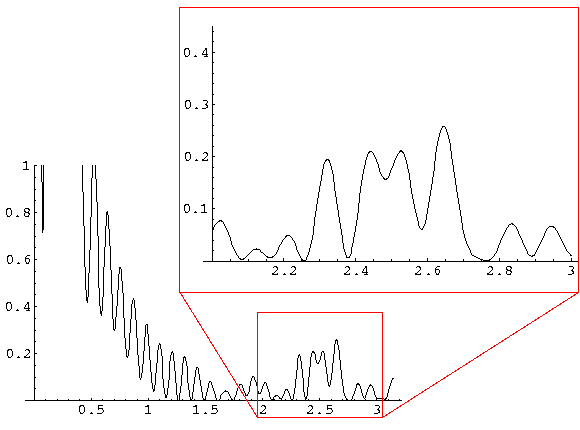
Finally, here is a set of cross-sections with increasing k' but with U0' also increased so that n=1.33. Note the main N=1 pure refraction peak, and the much small "rainbows" filled with interference.
k'=30:
k'=100:
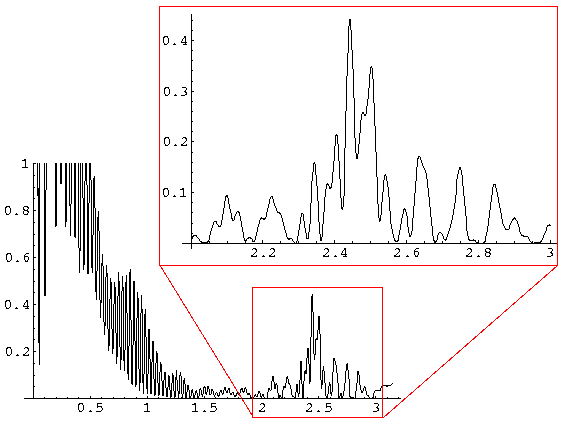
k'=300:
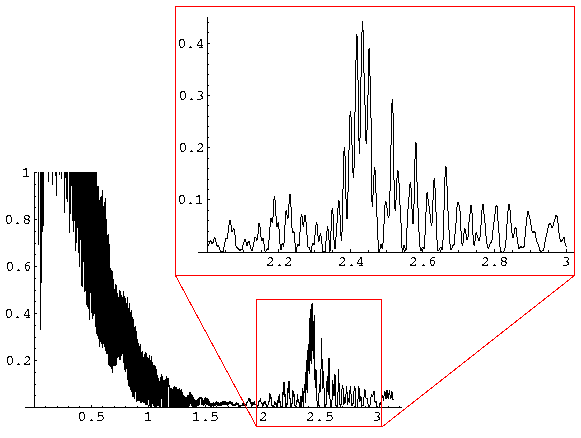
Here is a repeat of the classical equivalent: