Square Wells p.5

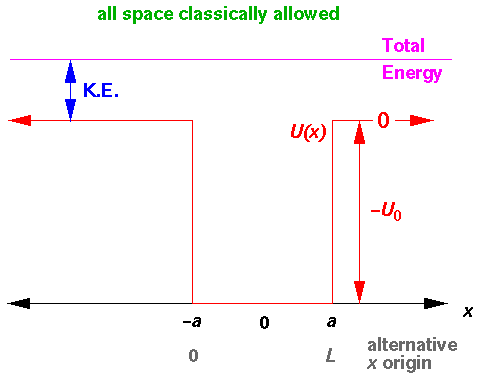
In order to study these states it's convenient to change the origin of energy. We'll shift all our energies up by the height of the well, so the top of the well becomes E=0 and the bottom of the well is -U₀. Shifting the zero of energy does not in any way change the states we found on the previous page, it just shifts the energy we assigned to them.

This is our new set-up for our square well:

Our aim here is do consider states with E>0, i.e., states with energies above the top of the well. Classically a particle moving along the x-axis from the left has constant kinetic energy (and hence speed) until it reaches the well. While on the first well wall (i.e., at x=0) the particle would experience a force accelerating it. It would move through the well at a constant speed faster than it had on the approach. When the particle hit the far wall it would experience a force slowing it to its original speed. The particle would then continue on its way to x=+. Pretty dull: straight-line motion, simply moving faster when "in" the well.

Schrödinger's equation is still as before:

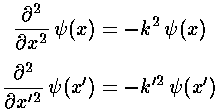
with well known solutions:

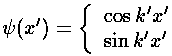
Note: outside the well U(x) is zero so:

k'²=E'

Inside the well we have more kinetic energy (and therefore momentum) so:

k'²=E'+U₀'

By the definition of wavelength for a trigonometric function: k=2/. Thus we have a shorter wavelength inside the well than out. Since k is the particles momentum, we have more momentum (and more kinetic energy) inside the well than outside.

As before we have different formula for the wavefunction inside and outside the well (different k means different functions). The game is to match at the well sides. Before we proceed, notice a nasty problem: we are going to have a sine or cosine wavefunction (or linear combination of the two) outside the well. Thus will not go to zero for large x and hence the solution cannot be normalized. There is no nice way out of this problem, instead here are four solutions, each one with problems:

1. Put the universe in a box. The problem is related to the fact that our spectrum of solutions is not discrete, i.e., we can find a solution for any real E>0. We can solve the normalization problem if we somehow force a discrete set of solutions. This could be done, for example, by imagining that the entire universe is surrounded by and infinite square well (whose spectrum we know is discrete). One imagines that an impenetrable wall a zillion light years from our little well should make no real difference, and it can make the calculations much easier. Actually instead of an infinite potential wall at nearly infinite distance, the usual method is to use period boundary conditions tied to a nearly infinite distance. Thus we would required that:

   (x+L)=(x)

   where L is some huge distance much bigger than any imaginable thing. In the absence of any forces, we can then get a discrete set of normalized wavefunctions:

   

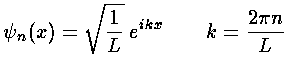
   I imagine this all sounds pretty outlandish, but it actually is a commonly used technique.

2. Change the normalization rules. Heretofore, we've required orthonormality of our energy eigenfunctions: that the total probability add up to 1 (normalized) and that different wavefunctions were orthogonal.

   

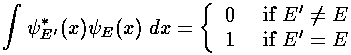
   In writing down orthonormality conditions we made a lot of use of the "Kronecker delta" 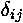that is 1 if i=j and zero otherwise. Now we invent the "Dirac delta function", which is kind of like the Kronecker delta, except for real numbers rather than just integers.

   

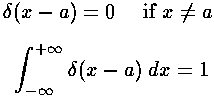
   The faint of heart (perhaps like your math TA) may blanch at these equations. Evidently the Dirac delta function is zero except at at single point (x=a), but the area under that point is 1! It must be that in some sense: (0)=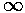. If we use the Dirac delta in our normalization:

   

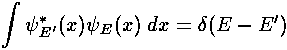
   we can have "normalized" functions that integrate out to .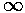

   The following relationship is very useful in making Dirac-delta normalized functions:

   

3. Make wave packets. If we actually had a wavefunction that represented a particle (i.e., a blob of probability) coming from infinity, approaching and interacting with the well, and returning to infinity it would look quite different from the simple sine and cosine functions considered above. Using Fourier analysis we could build up such a function from sines and cosines, but we would need to have a sum of sines and cosines with different wavelengths (i.e., different ks) for each term. Such a solution does not have an energy since different ks are involved. It would be normalizable however. It would also be quite complicated. One would also have to ask questions like: does the particular shape of the probability blob affect the general outcome (e.g., whether the particle ends up bouncing off the well or continuing through)? (We made these sort of superposition wavefunctions in our work on the 2-d fall problem.)

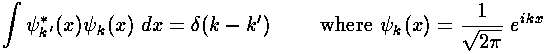
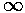4. Change the interpretation. Actual experiments rarely fire one particle at a well exactly once in the history of the universe. More commonly beams of particles are used. We seek then a wavefunction which we can interpret as a beam of moving particles. Not surprisingly such a wavefunction would have an infinite normalization because it would contain an infinitely long beam (to ±). What we need is a measure of beam current: the number of particles going by per second (we'll call this the flux). Since the particles are conserved, we need a relation between the probability density and the beams which move the probability around. (This is analogous to E&M where we had charge density and current density. There was a "continuity" equation that said: "if the charge density is changing it is being fed by a current density".) One can show that the following flux satisfies a continuity relation with our probability density.

   

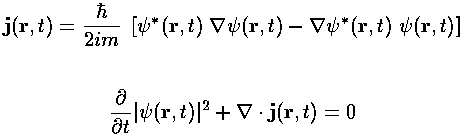
We begin by considering a wavefunction that is an eigenfunction of the momentum operator and hence has constant momentum:

=Ae^ikx

Plugging into the above definition for flux j, we have:

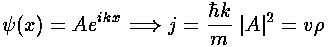
This relation should make sense. The momentum of the particle is p=k; p/m is the velocity v. We find that that flux is the probability density times the velocity (just as in E&M the current density was the velocity times the charge density).

Note that the flux is a constant even through the wavefunction is an oscillating function of position. Since the wavefunction is an energy eigenfunction (i.e., a solution to the time independent Schrödinger's equation), the probability density ||² doesn't depend on time. So the flux continuity equation says that that div(j) is zero. In just one dimension we have:

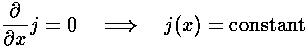
In our problem we expect to have both an incident beam of particles and a reflected beam of particles on the left side of the well. To the right of the well we expect a transmitted beam. Inside the well, we'll just use a linear combination of Schrödinger's equation solutions. We use here non-dimensionless variables and the alternative x origin with lhs well-wall at x=0. Our piece-wise solution with unknown constants A, B, R and T:

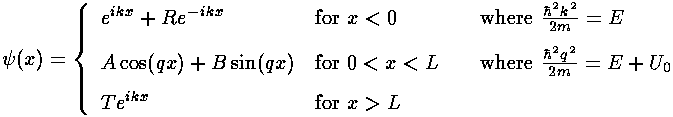
If we calculate the flux with this wavefunction we find:

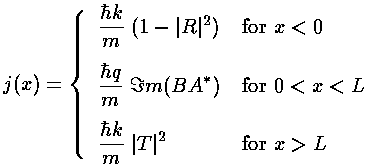
Notice that the flux for x<0 has a simple interpretation: the incident beam is moving to the right (+1), the reflected beam is moving to the left (-|R|²). Notice that all of these fluxes are just constants with no x dependence. Continuity requires that they be the same constant, so we learn, for example, that:

1-|R|²=|T|²

Now the reflection probability should be the reflected beam current divided by the incident beam current:

We're now set to match wavefunctions and wavefunction derivatives at x=0 and x=L:

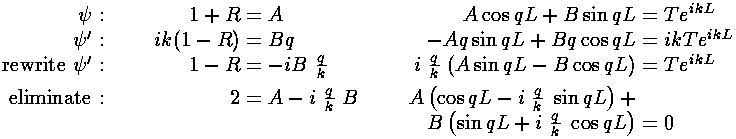
At this point I've eliminated unknowns T and R, and I've left you two equations to solve for the two unknowns A and B. After solving for A, you can find R=A-1

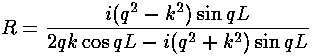
Here is a display of the resulting reflection probability (where highly reflecting is white and non-reflecting is black) in the natural coordinates of the problem.

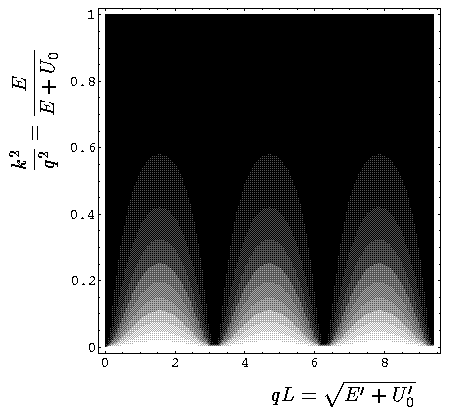
Here is a display of the reflection probability in terms of the natural experimental quantities E' U₀':

Recall that classically there is no reflection. In addition there is no reflection in the WKB approximation. Thus the non-zero reflection probability is a result of a non-WKB potential, i.e., one that changes substantially in one wavelength of the particle. We see the expected classical result of no reflection only for large energy, when E>>U₀. Note the zero reflection when qL=n, i.e., when the infinite square well version of the finite well has a bound state at the energy of the incoming particles. Experimentally one might hope to see oscillations in reflectivity just by raising the beam's energy. From the second plot see that it is difficult to get more than one good oscillation just by raising the beam energy.

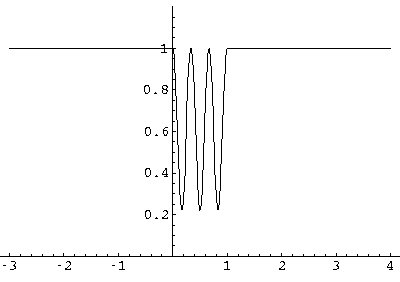
Since the wavefunctions are complex they are difficult to display as a x-y plot. We begin by displaying the real part of a low-energy (k²/q²=.5/7=.067) fairly reflective (|R|²=.64) wavefunction.

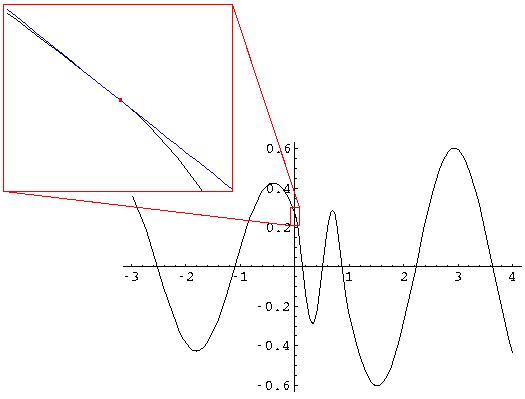
Note: the larger wavelength outside of the well. You may have thought you saw a slope miss-match at x=0. The insert shows that the slope is matched and that the second derivative of is much more negative inside the well compared to outside. The fact that the amplitude is bigger for x>L than for x<0 may lead you to the incorrect conclusion that the transmitted wave is larger than the incident and/or reflected wave. If we displayed the imaginary part of , you would see the oscillations for x<0 have a larger amplitude than those for x>L. This difference is cleared up by looking at the below probability density plot:

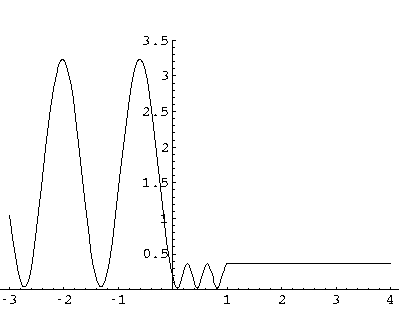
The probability oscillations for x<0 are the result of interference between the incoming and the reflected waves. It may look like the probability density actually goes to zero, e.g., near x=-1.3, but in fact the incoming and reflected waves cannot exactly cancel, since |R|<1. The minimums are (1-|R|)²=.04. The transmission probability looks to be a lot smaller than its actual value: |T|²=.36. Constructive interference between the incident and reflected wave makes the probability density large for x<0.

If we raise the energy, we can achieve the "resonant" zero reflection situation (k²/q²=2/7=.286, qL=3). Here is the real part of the wavefunction:

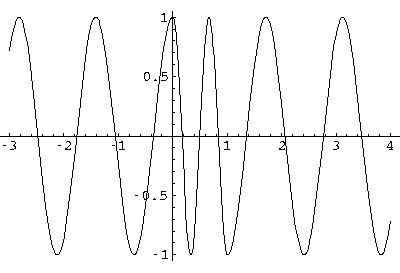
Here is the probability density:

Next