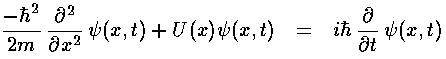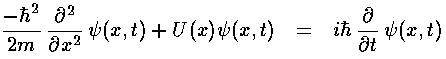Falling p.11

Falling in 2 Dimensions: y' Solutions

There is a problem with our y' solution: sinusoidal functions like sin(k_yy') or exp(i k_yy') maintain constant amplitude everywhere. With a probability density essentially the same over all of infinite space, how can there be a finite (in fact, unit) total probability? We say that these wavefunctions are not normalizable. In some sense this is not a surprising problem. If we have a free particle and know only its energy, it could be literally anywhere, which means that its probability of being in any finite region must be vanishingly small. As I note on future pages there is no single best solution to this problem. At this time, my choice is to side step this issue, by coming up with perfectly normalized solutions to Schrödinger's equation using the above unnormalizable solutions. This is a bit of a surprise: a superposition of unnormalizable solutions can be normalizable! Since I'll be using a superposition of several single-energy solutions, the solutions produced will not have a single energy. To deal with non-single-energy solutions, we must go back to the general time dependent Schrödinger's equation:

which has solutions that can be expressed using solutions to the (usual) time independent Schrödinger's equation:

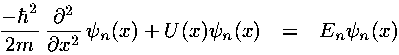Now we can produce time dependent solutions using (time varying) linear combinations of time independent solutions like:

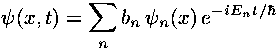See that each term in the above sum satisfies the time dependent Schrödinger's equation. Since the time dependent Schrödinger's equation is a linear equation, the sum of solutions is a solution (i.e., superposition).

Note that the above Schrödinger's equations have been particularized to 1d: x. I assume it is clear how to generalize these results to more dimensions. For example it should be clear that in our particular 2d-fall problem the time dependent solutions are linear combinations of solutions like:

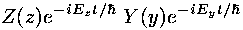
or in dimensionless form:

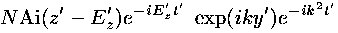
where the time unit for dimensionless time t' is /e, so E t/ = E' t'.

OK, our y' time dependent Schrödinger's equation has produced unnormalizable solutions like:

= exp(i ky') exp(-i k² t')

We seek a linear combination of these solutions to make a normalizable lump of probability. Classical physics suggests that this lump of probability should move at constant speed. Basically the idea is to have all the simple waves constructively interfere to produce the lump, and destructively interfere everywhere else. Finding this desired linear combination at t'=0 is easy once you remember Fourier transforms:

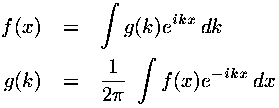
Thus if at t'=0 is to be a Gaussian lump of probability, say:

exp(-y'²)

we can use Fourier analysis to express such a function as a superposition (integral) of simple waves like exp(i k_yy'). At future times each simple wave has time dependence exp(-i k_y² t')) given by the time dependent Schrödinger's equation. Thus:

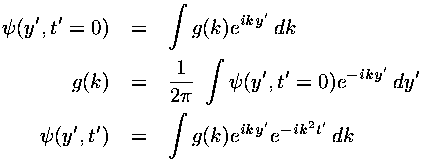
Three details: (1) According to Heisenberg's Uncertainty, the size of the wavefunction in space (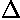y) affects the range of momentums (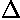p_y) that make up the wavefunction. If the particle has a large range of speeds, the wavefunction must separate out, i.e., expand. Thus to get relatively constant-sized wavefunctions we will want to enlarge the initial spread of the wavefunction. (2) Our wavefunction should be normalized so the total probability of it being someplace on the y' axis is one -- indeed producing such normalized solutions was the point in starting all this Fourier analysis in the first place. Thus we will want to consider t'=0 wavefunctions of the form:

= N exp(-y'²/4²)

where N is to be determined by the normalization condition:

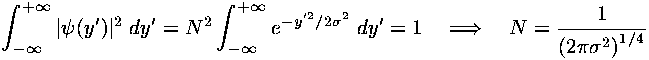
and turns out to be the standard deviation of the y' positions (i.e., 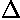y). (3) The above wavefunction is just a lump: it lacks waves. Of course we want a lump of probability, but we still want oscillation in the wavefunction. (Remember de Broglie's relationship between the wavelength of the wavefunction and the particle's momentum.) Something like:

= N exp(-y'²/4²) exp(i k₀y')

for constant wavenumber k₀, has the desired oscillation in wavefunction with no oscillation (just a lump) in probability density. g(k) can now be determined:

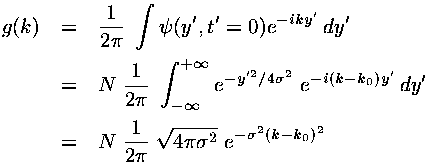
The amplitude of the simple wave in our superposition (i.e., g(k)) is large only when k is near k₀. If is large, k must be very near k₀ or g(k) will be small. This is Heisenberg Uncertainty: y' is proportional to ; k is inversely proportional to ; the product of the two is constant (in fact, ½). Note that we have employed the useful gaussian integral:

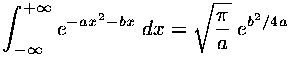
We can now calculate the fourier transform of g(k) producing a formula for (y',t').

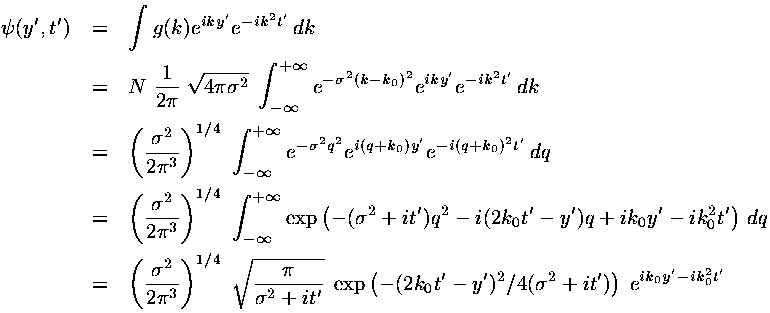
where we have calculated the integral using the change of variables:

q = k - k₀

and the above gaussian integral. I claim that this kind of messy solves our time-dependent Schrödinger's equation. This task is left for a problem.

To better understand the nature of this solution, it is helpful to calculate the probability density ||²:

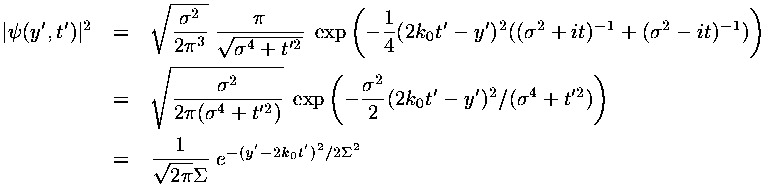
Note that the result is a lump of probability located at the moving position: 2k₀t' with a time-dependent width :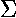

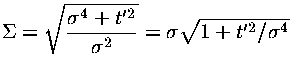
I'm getting tired of carefully distinguishing between the normal and dimensionless versions of variables (e.g., y vs y'). On future pages I'll drop the primes, but everything is to be considered the dimensionless quantity.