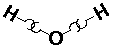
As an old discipline that has only in the 20th century found a working mechanics [quantum mechanics], chemistry is full of foma. One needs to understand a bit of this lore before you can open most any chemistry book.
In ionic compounds, like common table salt (NaCl), chemists would say that sodium is ionized: it has lost its outer 3s electron [which takes about 5.1 eV] becoming Na+, which has the same electron configuration as the inert gas Ne. Chlorine has gained that electron [which releases 3.7 eV], completing its 3p shell and becoming Cl-, which has the same electron configuration as the inert gas Ar.
In solid salt, the ions are packed closely together in a cubic array. [The coming together of the opposite charges more than makes up for the missing 5.1-3.7=1.4 eV of energy.] When salt is dissolved in water, the ions separate, and are surrounded by water molecules. Ionic compounds are often formed by taking something from the left hand side of the periodic table [things which like to lose electrons] and combining it with something from the right hand side of the periodic table [things which like to gain electrons].
Biological molecules are largely composed of atoms in the upper right side of the periodic table, e.g., C, N, O, and in addition hydrogen. Bonding in these molecules does not rely on charge transfer, instead the atoms "share" electrons. The result is called a covalent bond. Lacking a proper quantum mechanical explanation, early chemists thought of atoms as having hooks. H has one hook, O had 2, N three, C four.
Thus we can form common molecules like:
H20 (water): 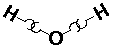
NH3 (ammonia): 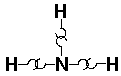
CH4 (methane): 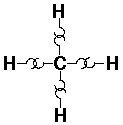
We can imagine using two hooks to form "double bonds":
CO2 (carbon dioxide): 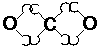
C2H4 (ethylene or ethene): 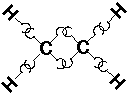
One flat paper it's hard to show triple bonds, but since the bonding symmetry is tetrahedral in carbon, there's no reason you can't stretch and interconnect three hooks.
A connection via hooks can be abbreviated with a line.
Thus we can form common molecules like:
H20 (water): 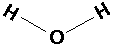
NH3 (ammonia): 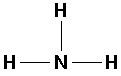
CH4 (methane): 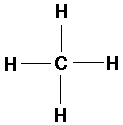
Double bonds are displayed with two lines:
CO2 (carbon dioxide): 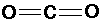
C2H4 (ethylene or ethene): 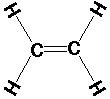
And triple bonds with three lines:
C2H2 (acetylene or ethyne): 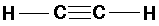
These "structural formulas" turn out to be an incredibly useful way of organizing/systematizing chemical knowledge. It has a basis in real measurements of molecules. For example, one can (to approximately 10% accuracy) record properties of bonds (like energies and lengths) independent of molecule:
| bond | energy eV | length Å |
|---|---|---|
| C-H | 4.4 | 1.1 |
| C-C | 3.6 | 1.5 |
| C=C | 6.4 | 1.3 |
C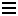 C C | 8.4 | 1.2 |
| O-C | 3.7 | 1.4 |
| N-C | 3.0 | 1.5 |
Note that generally multiple bonds store more energy and pull the molecule more closely together.
Note that the bond distance (= separation of nuclei) is comparable to the size of an atom. The "ball and stick" models of molecules overstate the length of the bonds...the atoms are really check-to-jowl in molecules.
Of course, quantum mechanics tells us that the electron wave will (generally) not be confined to the area between two atoms: it will spread throughout the molecular frame. Thus quantum mechanics has to work hard to explain how chemists can record the general properties of a bond type, independent of the surrounding molecule.
Many elements have compounds which suggest differing numbers of "hooks". For example, is sulfur like oxygen (H2O; H2S), like carbon (CO2; SO2) or does it have six hooks: (SF6 or SO4-2)? These molecules also have rather different shapes. The bond angle in H2S is 93°, SO2 is linear, SF6 is octahedral, and SO4-2 is tetrahedral. (In fact most elements in the period table display multiple "valence".)
Just before the quantum revolution the chemist G. N. Lewis invented a bonding representation (used mostly in the first two rows of the period table) called Lewis dot structures. The (at most 8) outer s and p electrons are arrayed around the chemical symbol. The gain or loss or sharing of electrons is displayed. The aim of bonding, Lewis said, is to produce the outer electronic configuration of a noble gas.
Thus we have the following possible reactions:
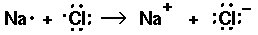
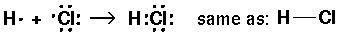
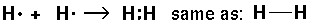
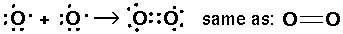
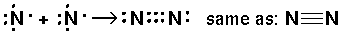
Thus single bond are displayed as a shared pair of electrons ":"
H20 (water): 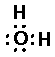
NH3 (ammonia): 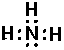
CH4 (methane): 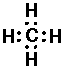
Double bonds are displayed as two pairs of shared electrons "::"
CO2 (carbon dioxide): 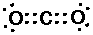
C2H4 (ethylene or ethene): 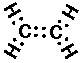
And triple bonds as three shared pairs ":::"
C2H2 (acetylene or ethyne): 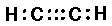
In Lewis's picture a covalent bond is a shared pair of electrons... today we would say a pair of electrons sharing a molecule-wide orbital. In some sense Lewis's picture explains why H, C, N, O, F, etc. have their observed valence, as the valence is the number of electron "holes" missing from the inert gas configuration...these holes need filling by sharing to produce the desired inert gas configuration.
If you're satisfied by "explanations" like the above, maybe you should be a chemist!
Lewis's picture raises lots of questions: why are the s and p electrons lumped together when be know because of l tilting the ns energy is below the np energy. While most simple covalent compounds have no net electron spin, some (e.g., O2) do...how could these electrons be "paired". What determines the bond angles, lengths, energies, etc.?
If we ignore l tilting (e.g., if we work with the H-atom where ns and np are degenerate) we can make 4 equivalent orbitals which in fact display the tetrahedral symmetry seen in CH4. This is called sp3 hybridization because one s and three p orbitals are involved.
The game is as simple as it is ultimately meaningless.
We start by forming the px, py, pz orbitals from our l=1 orbitals by recognizing the x,y,z coordinates in the Y1m:
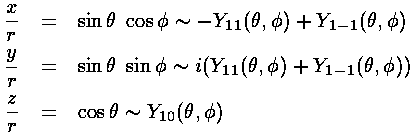
So
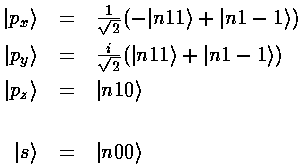
px, for example is just like pz (|n10>), except around the x axis instead of the z axis.
We now consider linear combinations of these orbitals given by a vector a (for simplicity we restrict ourselves to real number components for a).
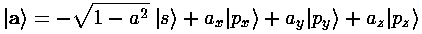
The p part of the sum produces a term proportional to a·r. Thus the p part of the sum is maximized when r points in the direction of a, and is zero when r is perpendicular to a. Since the s function is spherically symmetric, the result is a wavefunction that has its maximum in the direction of a...i.e., a wavefunction "pointing" in the direction of a. (Notice that the s term is designed to produce a normalized wavefunction, and that if we want to keep things real-valued |a|<1.)
So to produce wavefunctions pointing at the corners of a tetrahedron (so as to be ready to form a tetrahedral compound like CH4) all we need is a set of vectors {a,b,c,d} each pointing at one of the tetrahedron's corners.
Now the corners of a tetrahedron can be taken to be in the directions (1,1,1), (1,-1,-1), (-1,1,-1), and (-1,-1,1). (The angle between these directions is about 109°28'...i.e., the cosine of the angle is -1/3. Can you prove it?) The magnitude of our vectors is determined by the requirement that the wavefunctions be orthogonal. (Since we want equivalent orbitals, we take the magnitude of all four vectors to be the same as the magnitude of a).
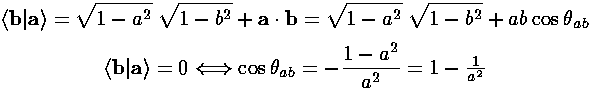
Thus we find |a|=3½/2, and our four sp3 hybridized orbitals are:
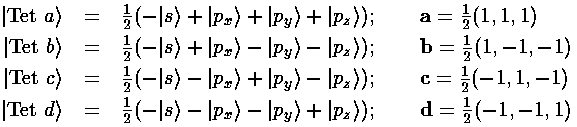
Here is what |Tet a> looks like in the z-xy plane (it is symmetric about the (1,1,1) direction ):
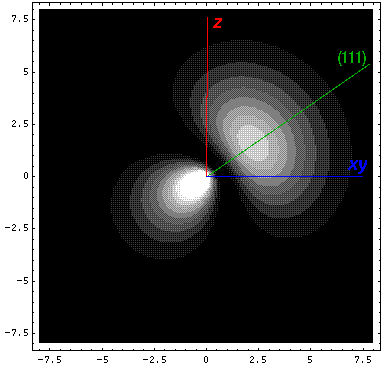
Here is a plot of the wavefunction along the (111) direction:
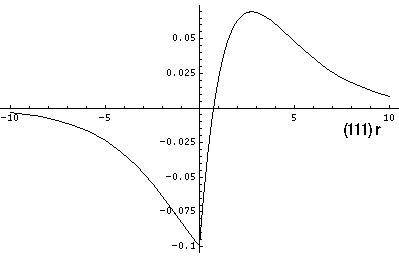
While these orbitals may make chemists feel better about the tetrahedral bonding in CH4, it does not have a basis in reality. In fact CH4 does not have four equivalent orbitals for its bonding electrons; instead it has 1+3...one low energy orbital symmetrically covering the entire molecule and then 3 higher-energy degenerate orbitals with one additional node. (This should remind you of the original s and 3 p orbitals.) Thus the suggestion in the structural formula and Lewis dot structure of 4 equivalent orbitals is wrong.
When carbon has a double bond (as in ethylene C2H4),
we find the three atoms surrounding the carbon in a plane with
approximately 120° bond angles. We can use the above game
to form 3 equivalent orbitals in the x-y plane. This is
called sp2 hybridization --- the
pz is not used so it is available to be involved in the
second bond of the double bond...in what's called a  -bond).
-bond).
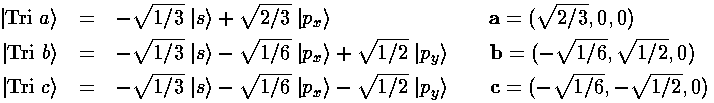
When carbon has a triple bond (as in acetylene C2H2)
or two double bonds (as in carbon dioxide CO2), we find
linear molecules. We can use the above game to form 2 equivalent
orbitals in say the z direction. This is called sp
hybridization, and we saw it in the Stark Effect. The two unused
p orbitals can be used to form two  -bonds.
-bonds.
Chemists acknowledge, in at least one case, the delocalized nature of molecular orbitals: the case of alternating double and single bonds, particularly as in benzene (also in porphyrin on the previous page). This goes under the rubric "resonance hybrids" or "aromatic compounds".