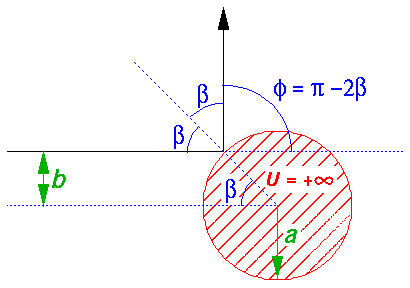
Classically we describe the situation in terms of impact parameter (b), which is the distance the incident particle would miss the origin in the absence of the potential. The impact parameter is closely related to the particle's angular momentum L and linear momentum p:
L= bp
where p=(2mE)½.
The above geometric construction tells us that the
scattering angle 
is simply
related to ß, which is in turn related
to the impact parameter:
b=a sin(ß)
Thus:
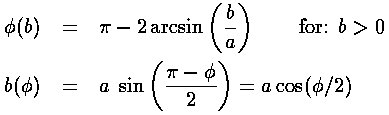
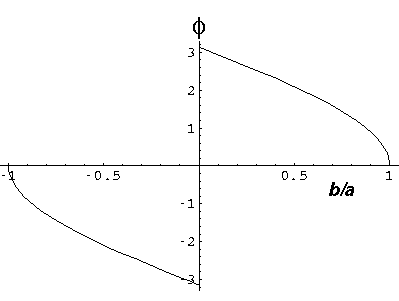
We assume now that our scattering center is
in a uniform stream of incident particles: an incident beam
of particles (I particles/sec) distributed over
some width (w) much larger than a.
We seek the rate at which particles are scattered into
a finite-sized detector which is located at a scattering
angle and detects particles in the
range: (,
+
).
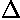
Clearly the rate particles are detected is proportional to
the flux (J=I/w) of particles in the beam.
(In fact clearly the total fraction of redirected particles
is 2a/w.)
We assume the beam is uniform so that:
the number/sec of beam particles in some range
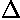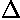b = I b/w
If we follow the trajectory of the large-b particles
and the small-b particles we find they end up going
in slightly different directions ()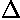
given by the above relationship (b).
We now define the differential cross section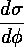 
:
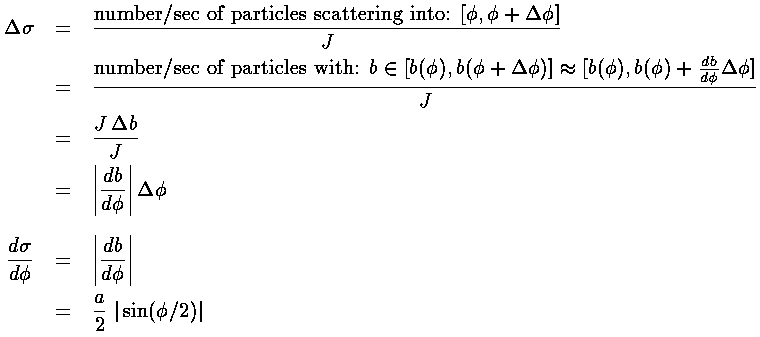
The differential cross-section is large in directions the particles frequently scatter.
Here is a plot of our classical differential cross-section. Note that the energy of the incident particles has no effect on their trajectory, so the classical differential cross-section is independent of energy.
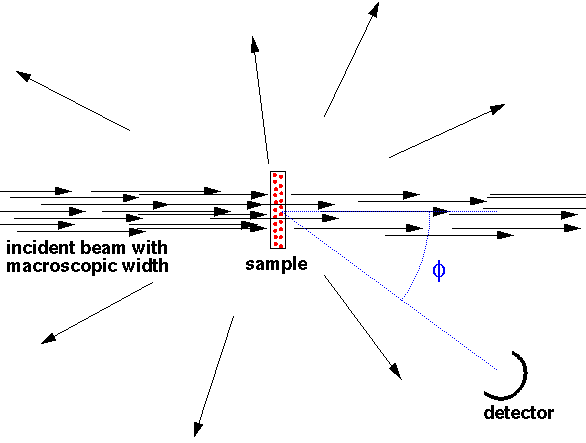
Clearly real experiments are not performed with just one scatter in the beam...that would waste almost all of the beam. Instead often a "thin" sample (thin enough so there is little multiple scattering) fully covers the beam and the cross-section is calculated from:
In the highest energy collision experiments, the "sample" is itself a high-speed beam of particles. The equipment is called a "colliding beam accelerator" or just a "collider".
Since the problem is symmetric,
we need to solve Schrödinger's equation in polar coordinates.
Every place the particle can be (i.e., r>a
or r'>1 in our dimensionless coordinates), the
potential is zero so as we have shown
the solutions are in terms of Bessel functions, e.g.,:
= Jm(k'r') cos(m)
where E'=k'2. We seek a solution that looks like a beam coming moving in the +x direction plus a scattered wave moving radially:
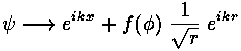
Of course, must also satisfy the boundary condition
and be zero at r'=1.
We can extract the cross-section from this formula. The flux in the
beam is 
k/m. For the scattered part of the
wavefunction, in the limit of large r, the radial flux
(jr=j·r/r) is |f|2k/mr.
Thus the number/sec of particles going through a distant radial surface of length
r d is |f|2(k/m)d.
The differential cross-section is then:
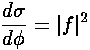
We begin by noting that since exp(ik'x') is a solution to the totally free (U=0 everywhere) Schrödinger's equation, it can be expressed in terms of solutions to the totally free Schrödinger's equation in polar coordinates:
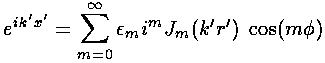
where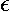 
m is a shorthand:
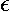0=1, all other 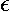m=2.
Now instead of having Jm, we would like to have solutions
to our actual Schrödinger's equation, i.e., Bessel functions, but zero at
r'=1. We proceed by expressing Jm in terms
of its incoming and outgoing radial waves (i.e., in terms of Hankel functions).
We expect that the incoming wave is not modified by the potential, but the
outgoing wave may be modified by the potential. Now since the outgoing flux
must still equal the incoming flux (i.e., probability must be conserved for
each value of angular momentum m), we cannot not change the amplitude
of the outgoing wave, only its phase. Thus we insert a phase factor
which is adjusted to match the boundary condition.
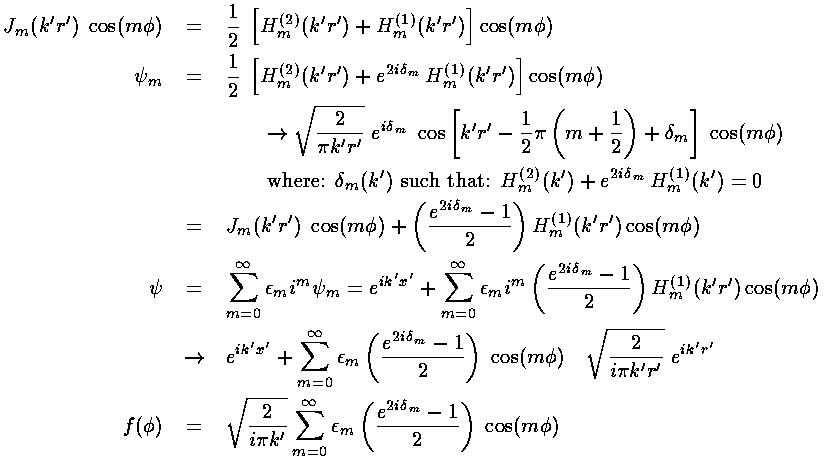
We have produced a solution
that looks like exp(ik'x') plus a scattered wave and
satisfies the boundary condition at r'=1. And we have
an expression for f (and hence the cross-section) in terms of
the phase shifts: 
m.
We note that the equation for the energy dependent phase shifts
m
are not as formidable as they may appear; they are simply the phase
of H(2)(k') less 90°. We show below
the asymptotic forms for the phase shifts obtained simply by substituting
in the asymptotic forms for Jm and Ym
previously given.
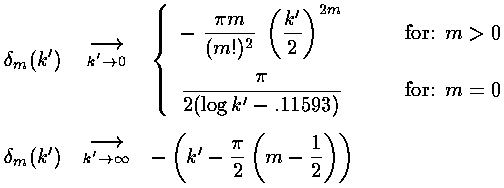
Here are plots of the phase shifts for m=0,1,2. The red curves display the low energy approximations, the blue curves display the high energy approximations.
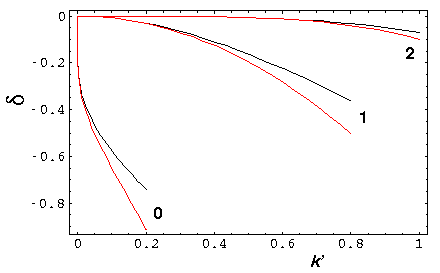
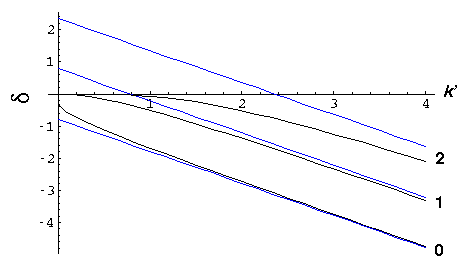
At low energy, all the phase shifts approach zero. but m=0 is the slowest to approach zero, so it is responsible for almost all of the scattering. At low energy we have "s-wave" scattering because
b= L/p
so non-zero angular momentum, low energy incident particles "miss by a mile". Only the zero angular momentum particles have a chance to touch the potential. Alternatively, we could say that the centrifugal potential of non-zero angular momentum incident particles reflects low energy the particles before they can approach the potential. As you would expect for "s-wave" scattering, the scattering is isotropic. Finally one might say that the De Broglie wavelength (h/p) of the beam particles must be smaller than the potential well (a) if it is to "see" the potential well.
At high energy, all the phase shifts for m<k' are "large". We proceed to numerically sum the series for f and find where the scattered particles are going.
Here are plots of the differential cross-section at k'=.1, .3, 1, 3, and
10. Note we progress from a large uniform cross-section at low energy,
to a cross-section that agrees with the classical result for moderate ,
but in addition has a strong peak near =0. The strong peak is called
the diffraction peak. It exists because the scattered wavefunction must
both produce flux at various scattering angles and subtract flux from the beam,
i.e., form a shadow at =0 by interfering with the exp(ikx)
plane wave.
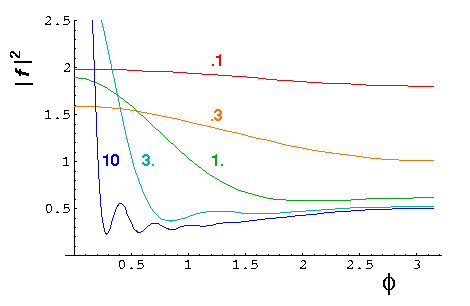
At high energies one can show [e.g., Morse & Feshbach Part II] that the differential cross-section is approximately
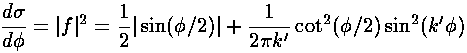
where the first term is the classical result and the second term forms the shadow (i.e., the diffraction peak).
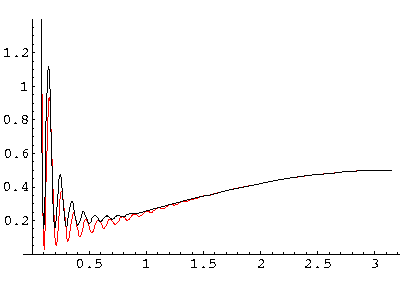
Here is a plot for k'=30 of both the exact result (black) and the above approximation (red).
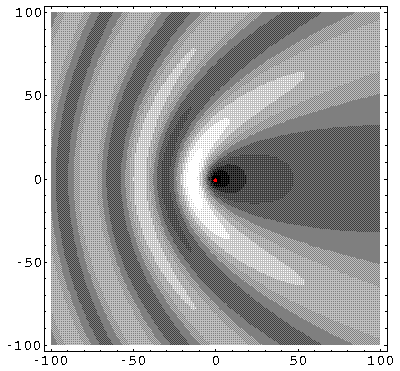
We can display the probability density from our wavefunction.
For k'=10, note the clear shadow behind the well.
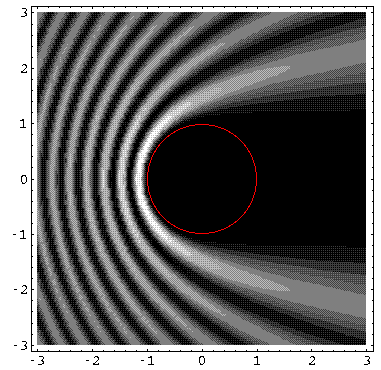
For k'=1 the shadow is much reduced because the longer wavelength waves diffract around the well. (Note the displayed region has been increased, so the 10× longer waves can fit in the picture.)
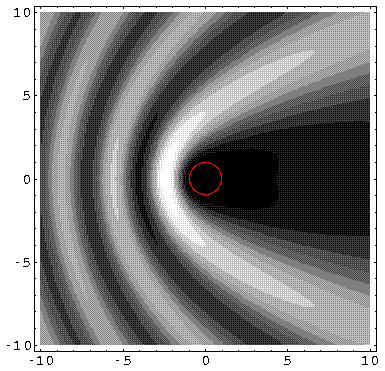
k'=0.1: (Note the displayed region has been increased, so the 10× longer waves can fit in the picture.)
