Square Wells p.7

Two Dimensional Square Wells

We consider here a rectangular "infinite square well". The potential is 0 inside a rectangle with diagonal points of the origin and (L_x,L_y) and infinite outside the rectangle.

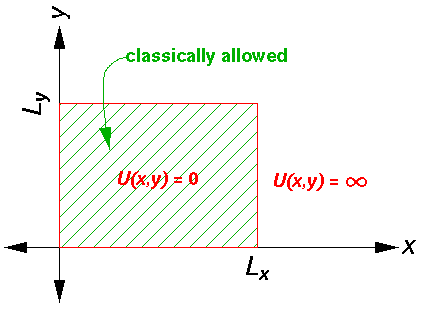
(We use here the "alternative origin" rather having the well centered on the origin.) As before we have the "boundary" condition that be zero in the infinitely disallowed region outside the rectangle. Inside the rectangle, where the potential is zero, we have the Schrödinger's equation:

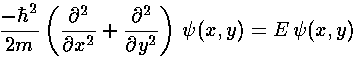
Since the Hamiltonian is the sum of two terms with totally separate variables, we try a product wavefunction:

=X(x)·Y(y)

As usual with separation of variables, the Schrödinger's equation separates into two terms, one only in x the other only in y:

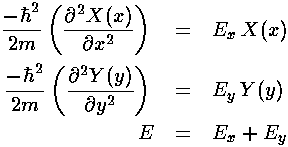
These familiar differential equations have the usual solution:

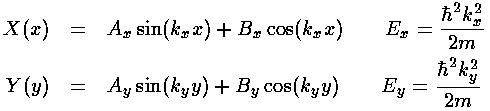
Now we apply our boundary conditions

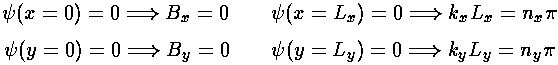
The resulting normalized wavefunctions are:

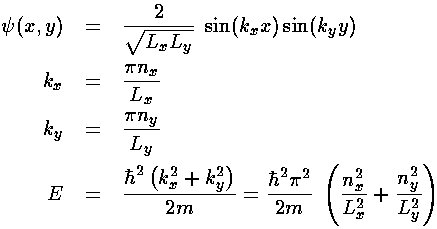
Here is a plot of the probability density for a typical wavefunction: n_x=2, n_y=4, for L_x=4, L_y=3:

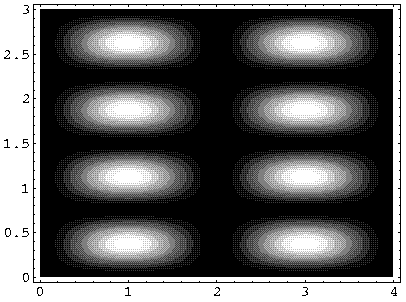
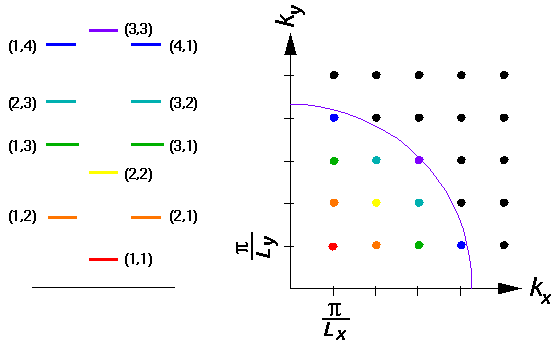
It is often convenient to describe wavefunctions in terms of "k-space" or "n-space", that is we label wavefunctions by k=(k_x,k_y) vector or by n=(n_x,n_y). In either case there is a lattice of points in the plane each one of which represents a possible wavefunctions. In the case of n-space, the lattice consists of those points with whole number x,y values. In the case of k-space, the lattice points are spaced by /L_x, /L_y. (k-space goes by many different names. The momentum p=k is closely related to k, hence "momentum space". k is also closed related to "reciprocal lattice space". 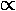Since k=2/, k is often called a "wave number" [danger: the same thing without the 2 is also called wave number].) The main idea for us is that E |k|²

Here is an energy level diagram showing the relationship between k-space, n=(n_x,n_y) and the energy for a square (L_x=L_y) square well.