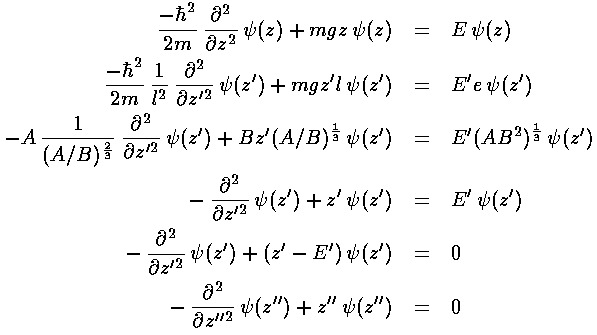
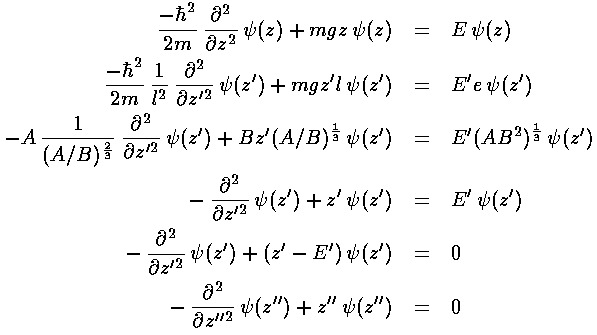
This last equation is the differential equation for Airy's function (see for example, Abramowitz & Stegun, §10.4 p. 446). Thus the wavefunction is Ai(z'') = Ai(z'-E') = Ai(z/l-E/e). Below is a plot of the Airy function Ai(x) from x=-10 to 5.
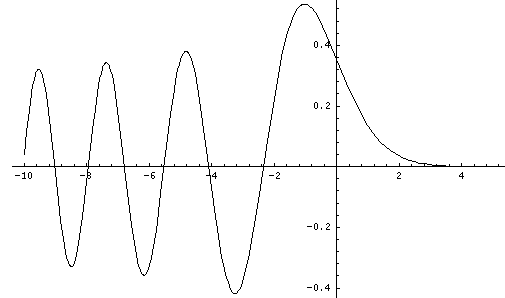
By choosing the Airy function Ai(x) (rather than Bi(x) ) we have required that the wavefunction approach zero for large x. An additional boundary condition is that the wavefunction be zero for z=0, i.e, Ai(-E')=0, i.e., -E' must be a root of the Airy function. Compare the above graph of Ai to the below table of roots of Ai.
| n | E' (-rootn) |
|---|---|
| 1 | 2.33810 |
| 2 | 4.08794 |
| 3 | 5.52055 |
| 4 | 6.78670 |
| 5 | 7.94413 |
| 6 | 9.02265 |
| 7 | 10.04017 |
| 8 | 11.00852 |
| 9 | 11.93601 |
| 10 | 12.82877 |
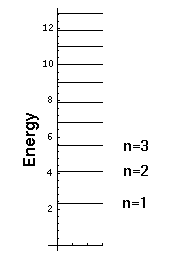
Notice that we have a discrete set of energy levels, i.e., energy is quantized and the particle can have only the above energies. Quantum mechanics says energies between these levels will not be seen in nature. A discrete set of levels is expected if the particle is confined to a region.
Notice that the energy levels become closer together as you go up in energy. (Energy spacing (i.e., differences) are quite important as (1) that is what is observed in emitted photon energies and (2) that is what is related to the classical period.)