) are given.
Consider the following example of the H(x) function
for a 10g H-atom wavefunction.
H(x)=240240 - 120120 x + 21840 x2 - 1820 x3 + 70 x4 - x5
- What is l? nr?
?
- Show that this H satisfies the H differential equation.
- Show that the coefficients satisfy the recursion relation.
- This H is not quite a Laguerre polynomial...it is off by an overall factor. What is that overall factor?
- <1/r>=1/n2
- <r>=½[3n2-l(l+1)]
- <r2>=½n2 [5n2+1-3l(l+1)]
- <1/r2>=1/[(l+½)n3]
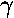, X-ray,
UV, visible, IR, microwave, radio).
- H-atom: 2
1
- H-atom: 3 2
- H-atom: 4 3 ;
3
- H-atom: 5 4 ; 4
- H-atom: 11 10
- H-atom: 101 100
- C-atom: 2 1
- U-atom: 2 1
- the size of a "bucky ball" C60: r=5Å
- the size of a big bacteria cell: r=0.5µm
- the size of a pin head: r=0.4mm
=N(|100> - 2|200> + i|210> + |211>)
where |210> means the wavefunction has n=2, l=1, m=0.
- Find the normalization N.
- Find the expectation value of energy.
- Find the expectation value of r (use Mathematica).
There are four "x-y" graphs on this page. The first two (with x-axis labels z & x) are very similar and the next two (with x-axis labels x & z) are very similar. Why are the pairs similar? why are they different? Describe how changing nr would change these graphs.
(l+½)2
relation, simply change the potential from r2 to
1/r. Now find the WKB energies for the H-atom.
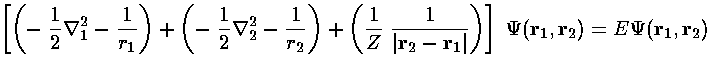
and the trial wavefunction: =
exp[-a(r1+r2)]
Here is the process of finding the expectation value as a function of a and then finding the lowest such upper bound:
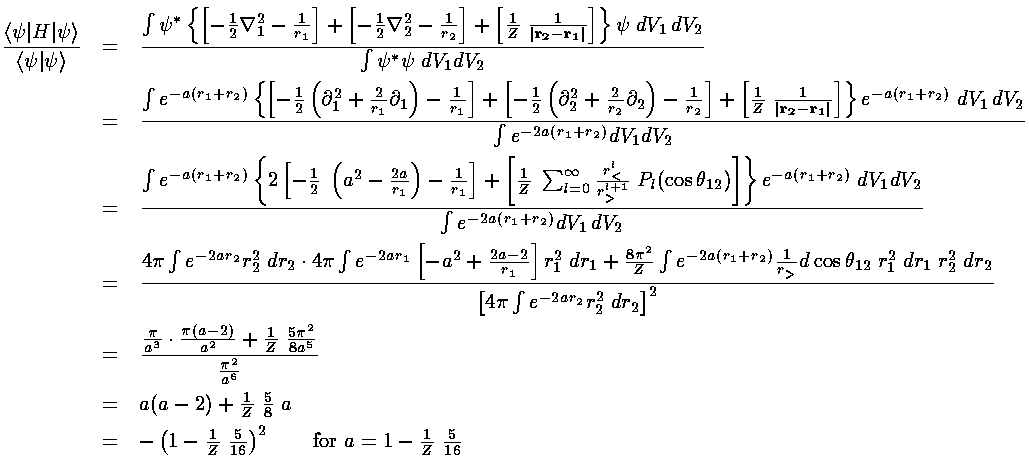
Justify each step in the above derivation. Some things to consider:
How did the derivative terms come about, e.g., what happened to
the angular part of the Laplacians. In line 1 we have three terms in
square brackets "[]", on the third line its just two...what happened?
The term that starts as the third square bracket term become an infinite sum
and then just the first term in that sum...what happened? What are the
Pl and what is the argument: 
12?
Explain how each "dV" was eventually replaced and why.
Evaluate each integral with Mathematica and verify the
results.
| System | calculated energy | energy in (eV) | System less one electron | energy of that ion (eV) | calculated ionization energy (eV) | experimental ionization energy (eV) |
|---|---|---|---|---|---|---|
| H- | -.473 | -12.86 | H | -13.61 | -.75 | .75 |
| He | -.712 | -77.49 | He+ | -54.42 | 23.1 | 24.6 |
| Li+ | -.803 | -196.54 | Li+2 | -122.45 | 74.1 | 75.6 |
For comparison, ignoring the interaction, each 1s electron would give a binding energy of ½, so for 1s2 we would have an energy of -1. For large Z we approach that limit.
The variational calculation is fairly accurate, its estimated energies are about 1½ eV too high. (It is, after all, just an upper limit on the energy.) Unfortunately that 1½ eV difference is critical for the existence of the ion: H-. By our calculation H- is less strongly bound than H and so should spontaneously dissociate. But it turns out that H- is stable and is critical for understanding the opacity of the atmosphere of the Sun. Furthermore, H- is difficult to make in the lab so calculation was the basis for understanding this ion. In fact, discrepancies between early calculations and observational evidence on the Sun's radiation pointed out the inaccuracies of the then-existing wave functions for H-.
Thus improved calculations of H- properties were very much on the agenda of physics in the 1950s. Our variational calculation allows the electrons expand away from the nucleus (as one would expect, given the partial shielding by the other electron) [i.e., a has been reduced from the hydrogen value of 1]. One expects an additional effect: the electrons should avoid each other. It turns out that we can to a bit better if we allow the electrons to have different "orbital radii"...i.e., to use a trial wavefunction like:
exp[-ar1-br2] + exp[-br1-ar2]
Use this wavefunction and show that the H- ionization energy is positive (i.e., H- is more stable than H+e-)
We consider here a trial wavefunction:
(exp[-ar1-br2] + exp[-br1-ar2]) (1+c|r2-r1|)
It is a mess to find the energy expectation value, but here is the result in Mathematica form (so you can cut and paste):
e=(-2*a^11*b^2 + a^12*b^2 - 16*a^10*b^3 + 8*a^11*b^3 - 56*a^9*b^4 +
29*a^10*b^4 - 204*a^8*b^5 + 64*a^9*b^5 - 426*a^7*b^6 + 226*a^8*b^6 -
426*a^6*b^7 + 368*a^7*b^7 - 204*a^5*b^8 + 226*a^6*b^8 - 56*a^4*b^9 +
64*a^5*b^9 - 16*a^3*b^10 + 29*a^4*b^10 - 2*a^2*b^11 + 8*a^3*b^11 +
a^2*b^12 - 6*a^11*b*c + 3*a^12*b*c - 48*a^10*b^2*c + 24*a^11*b^2*c -
170*a^9*b^3*c + 85*a^10*b^3*c - 360*a^8*b^4*c + 176*a^9*b^4*c -
1232*a^7*b^5*c + 165*a^8*b^5*c - 2000*a^6*b^6*c + 1147*a^7*b^6*c -
1232*a^5*b^7*c + 1147*a^6*b^7*c - 360*a^4*b^8*c + 165*a^5*b^8*c -
170*a^3*b^9*c + 176*a^4*b^9*c - 48*a^2*b^10*c + 85*a^3*b^10*c -
6*a*b^11*c + 24*a^2*b^11*c + 3*a*b^12*c - 6*a^11*c^2 + 3*a^12*c^2 -
48*a^10*b*c^2 + 24*a^11*b*c^2 - 171*a^9*b^2*c^2 + 86*a^10*b^2*c^2 -
364*a^8*b^3*c^2 + 184*a^9*b^3*c^2 - 536*a^7*b^4*c^2 + 269*a^8*b^4*c^2 -
2363*a^6*b^5*c^2 + 48*a^7*b^5*c^2 - 2363*a^5*b^6*c^2 +
2868*a^6*b^6*c^2 - 536*a^4*b^7*c^2 + 48*a^5*b^7*c^2 - 364*a^3*b^8*c^2 +
269*a^4*b^8*c^2 - 171*a^2*b^9*c^2 + 184*a^3*b^9*c^2 - 48*a*b^10*c^2 +
86*a^2*b^10*c^2 - 6*b^11*c^2 + 24*a*b^11*c^2 + 3*b^12*c^2)/
(2*(a^10*b^2 + 8*a^9*b^3 + 28*a^8*b^4 + 120*a^7*b^5 + 198*a^6*b^6 +
120*a^5*b^7 + 28*a^4*b^8 + 8*a^3*b^9 + a^2*b^10 + 3*a^10*b*c +
24*a^9*b^2*c + 86*a^8*b^3*c + 184*a^7*b^4*c + 823*a^6*b^5*c +
823*a^5*b^6*c + 184*a^4*b^7*c + 86*a^3*b^8*c + 24*a^2*b^9*c +
3*a*b^10*c + 3*a^10*c^2 + 24*a^9*b*c^2 + 87*a^8*b^2*c^2 +
192*a^7*b^3*c^2 + 294*a^6*b^4*c^2 + 1872*a^5*b^5*c^2 +
294*a^4*b^6*c^2 + 192*a^3*b^7*c^2 + 87*a^2*b^8*c^2 + 24*a*b^9*c^2 +
3*b^10*c^2))
Find the minimum of this function. You should find a reasonable value for the ionization potential of H- near 0.7 eV. A 24 parameter trial wavefunction (published in 1956) gave an ionization potential of: 0.7545 eV.
1 is shifted
by 1 Å. (Approximate the coulomb field of the ion: assume
the ion's E field at the atom's nucleus is uniform throughout the
atom.)
Using the parabolic solution to the Stark Effect, find how close an ion could come to a n=100 H-atom without the calculated shift being large enough to ionize the atom.