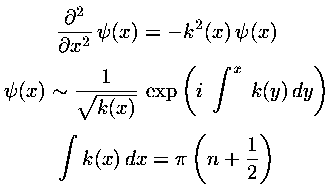
The WKB approximation is most commonly used to approximate large n eigenenergies in bound state problems. Here is the summary of the usual WKB results:
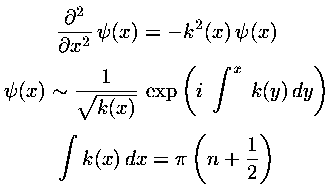
For this bouncing ball problem, WKB produces:
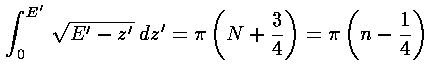
where in our dimensionless variables k2=E'-z', and the usual WKB quantum number N running 0,1,2,3,... has been replaced with our quantum number n running 1,2,3,4,... (i.e., N=n-1). Notice also that the usual WKB ½ has been replaced with ¾...why is that? The resulting formula for E'n:
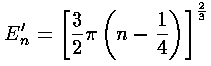
is the start of a well known formula for the zeros of the Airy function (e.g., Abramowitz & Stegun, §10.4.94&105 p. 450). Abramowitz & Stegun report (for large n) the fractional error in this result is of order: .005/n2.
The Rayleigh-Ritz is most commonly used to give an upper bound for the groundstate eigenenergy. Consider, for example, the following guess at the groundstate wavefunction (a "trial" wavefunction): f(z')=z'(a2-z'2) for 0<z'<a and otherwise f(z')=0. If we evaluate the expectation value of the Hamiltonian we find:
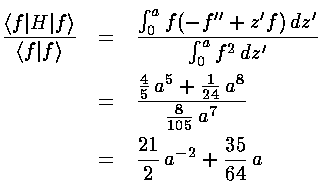
This expectation value is guaranteed to be above the groundstate energy for every a. To get the lowest upper-bound, we want to find the value of a that produces the smallest expectation value; that value of a should produce the wavefunction and expectation value closest to the actually groundstate wavefunction and groundstate energy. In this particular example, we can find the minimum value of the expectation value by taking the derivative w.r.t. a and setting the result equal to zero:
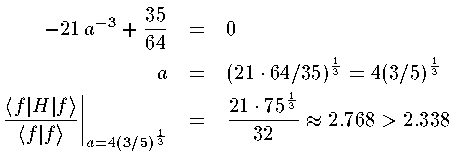
Better guesses for our approximate wavefunction f(z'), produce better (closer) results. For example, the guess:
f(z')=z' exp(-az'),
produces a upper bound for the groundstate energy of 2.476 just 6% above the correct result. In the below plot the "best a" trial wavefunctions are plotted (blue: the polynomial; red: the exponential) and compared to the exact Airy groundstate wavefunction (black)
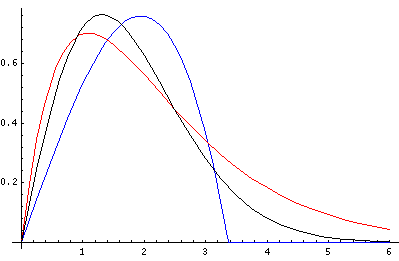
Note that a fairly approximate trial wavefunction (e.g., red), produced moderately close energy. This is the "quadratic accuracy" that makes Rayleigh-Ritz so useful for eigenenergies (but not nearly so useful for wavefunctions).
We consider here the simplest version of perturbation theory: time independent, first-order, and non-degenerate. To start the perturbation theory game we need a solution to a Schrödinger's equation. Perturbation theory then approximates the effect of small additional forces (beyond those in the Schrödinger's equation already solved) on eigenenergies and wavefunctions. For example, the already-solved-Schrödinger's-equation might be for the hydrogen atom, the small additional force might be an external magnetic field, and our aim to calculate the small Zeeman shift of energy levels in the (slightly) changed situation of strong nuclear attraction plus small magnetic bending.
The result of perturbation theory is that the small shift in energy is given by the following formula:
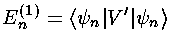
That is that the first order shift in the energy of the
nth energy eigenfunction
(En(1)) is just the expectation value
of the additional potential (V') using the nth
energy eigenfunctions (
n)
(i.e., the shift in energy is just the
average value of the potential for that eigenfunction).
Consider then the (fairly bogus) example of a small additional constant force in our bouncing-ball problem. It's "fairly bogus" because we can exactly solve this problem, but thats the point: we can then compare the perturbation theory approximation to the exact answer.
We consider then a potential:
V(z)=mgz(1+
)
where represents the small additional
perturbing force (i.e, V'(z)=mgz)
Since the problem remains that of a linear potential, the solution is
exactly as above (Airy function, etc.) but with modified scales
l and e. Thus the eigenenergies are:
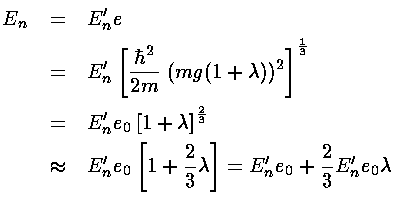
Hence to verify perturbation theory we must show the following:
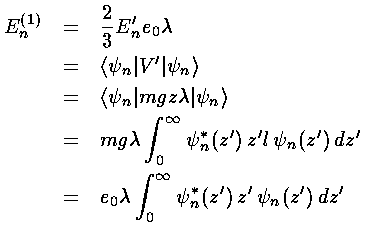
or simply:
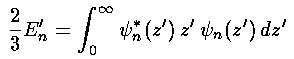
Proving that the Airy functions satisfy the above for every n looks to be a chore, but the Virial theorem (Saxon p.115&297, Gasiorowicz p.208, Schiff p.180) comes to our rescue and proves the above.