H-atom p.3

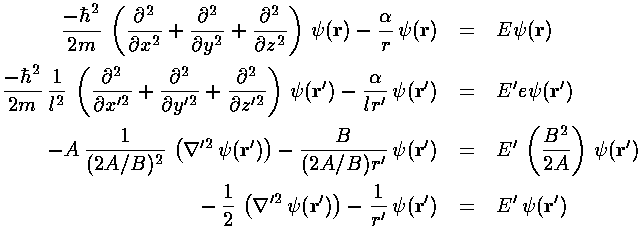
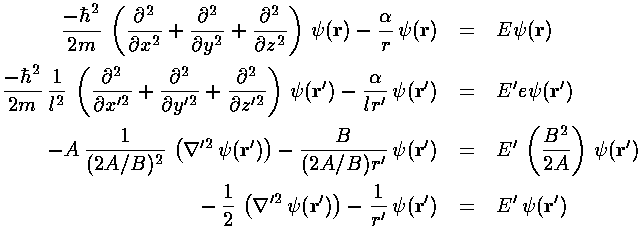
Since the problem is rotationally symmetric rather than square-symmetric, it makes more sense to use a coordinate system that reflects the symmetry in the problem. Hence, I'd like to solve this problem is spherical coordinates (r'--).

Changing coordinates changes the Schrödinger's equation to:

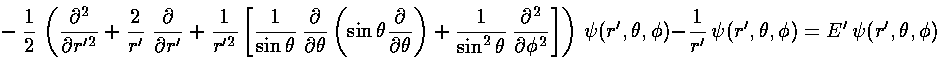
The stuff in the square brackets (with the overall minus sign) is the (dimensionless) angular momentum squared operator: L'². The eigenfunctions of this operator are degenerate, so there is a choice to make in defining the basis states. In physics folks conventionally use the Y_lm, which are simultaneously eigenfunctions of both L'² and L'_z:

L'² Y_lm = l(l+1) Y_lm

L'_z Y_lm = m Y_lm

Chemists not uncommonly use a different basis which has the advantage that the functions are real, but the disadvantage that they do not display spherical symmetry.

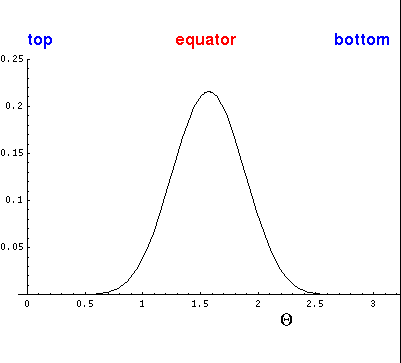
The probability density Y_lm^*Y_lm is independent of ("cylindrically symmetric" for a cylinder whose axis is aligned with the z axis) so we only need to concern ourselves with their dependence on . As you would expect if the angular momentum is aligned with the z axis (so m=l) the probability should mostly be in the x-y plane, i.e., =/2=90°. Below is a plot of the probability density for l=m=5.

Here is the corresponding plot just as a function of .

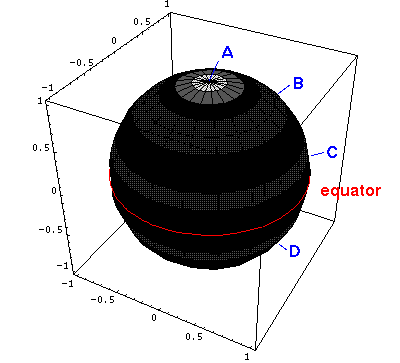
On the other hand, if m=0, the angular momentum vector must be in the x-y plane and the particle must be moving perpendicular to the angular momentum vector and hence in part in the z direction. For example, if L~i (i.e., the angular momentum vector is in the x direction), we expect motion to be in the y-z plane. The m=0 solutions are essentially superpositions of all possible orientations of L in the x-y plane. 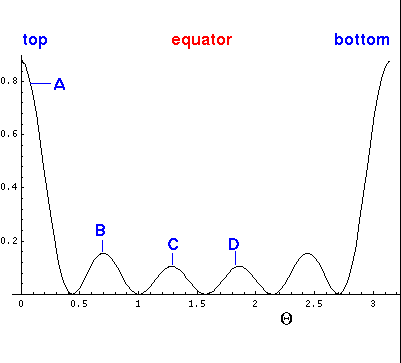What survives the superposition is: (1) a big amplitude on the z-axis where all orientations contribute, (2) oscillation (motion) in and (3) uniform distribution in . Below is a plot of the probability density for l=5, m=0.

Here is the corresponding plot just as a function of .

(Here is a bit more information about the Y_lm and other choices.)

Seeking a solution where the dependence on r' factors with all the , dependence in Y_lm ("separation of variables"), i.e., =R(r')Y_lm we find:

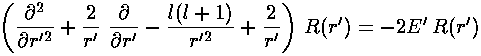
As usual we have to work a bit to solve for the r' wavefunction. Start by seeing how the equation must work for large r'. Most of the terms vanish for large r'. Only the first term on the left has a chance of equaling the term on the right. Ignoring the (small) terms, we seek to find the form for that solves the differential equation for large r' (remember E'<0 so -E'=|E'|)

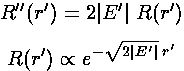
Note that for large r', is a function of |E'|^½r'. We take this as a hint to use a variable proportional to |E'|^½r' everywhere. Thus we define

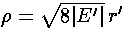
and rewrite our r' differential equation in terms of . To do this divide the above r' differential equation by 8|E'|, yielding:

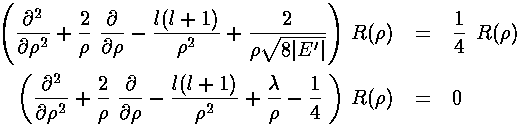
Note that we have eliminated E' in favor of a new constant

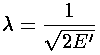
For small only the derivative terms have a chance to match the ever growing l(l+1)/² term. If we try a power-law solution ⁿ

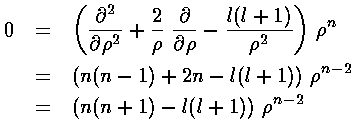
we find n=l or n=-(l+1); the former is not singular as nears 0

Factoring out all the required behavior for large and small , we hope to find a simple function (polynomial with luck) H() that contains the behavior for intermediate .

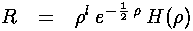
Now the work begins: we need to express all the derivatives of R in the differential equation in terms of derivatives of H

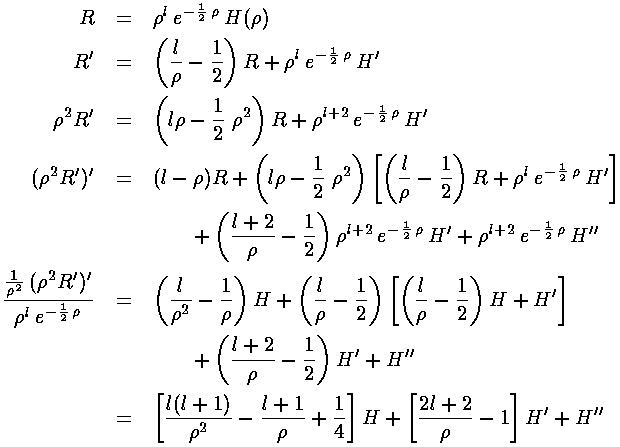
Using these derivatives in the R differential equation gives use what we hope is an easier to solve differential equation for H:

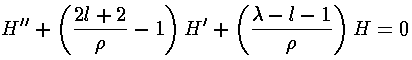
If we now try to write H as a polynomial:

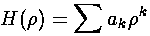
we can plug the polynomial form into the differential equation:

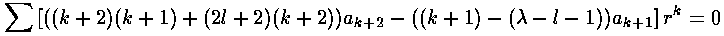
The result is a two term recursion relation (i.e., the result has just two as so, for example, given a₀ we can calculate a₁, from which we can calculate a₂, etc. until we're done.)

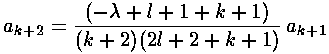
It is convenient to shift the recursion relation down one (i.e., kk-1):

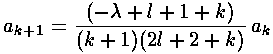
It turns out that the polynomial must end if the wavefunction is to be normalizable. One can show that the non-terminating sum gets at least as big as exp(+), so instead of going to zero for large gets big like: exp(+/2). The only way the sum can end is if the numerator of the recursion relation is zero, i.e., if is an integer n (which we call the principal quantum number). n_r (called the radial quantum number) is the highest power in the H polynomial.

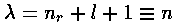
Now that we know , we can find E:

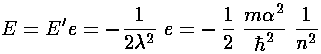
In the the case of an atom, we can express the force constant in terms the the number of protons in the nucleus (Z) and the charge on the nucleus (in cgs units) (e): =Ze². So:

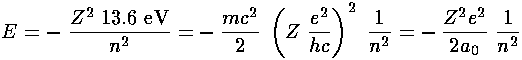
We also find a simple relationship between and r':

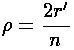
Note that if we had tried for a polynomial solution for R itself (rather than factoring out the ^lexp(-/2) first), we would get an (unsolvable) three term recursion relation.

The polynomials we have been calling H are Laguerre polynomials (see for example, Abramowitz & Stegun, §22 p. 771 or Szegö Ch.V).

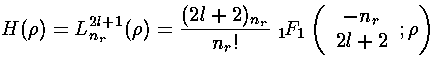
n	E'
1	-0.500
2	-0.125
3	-0.056
4	-0.031
5	-0.020

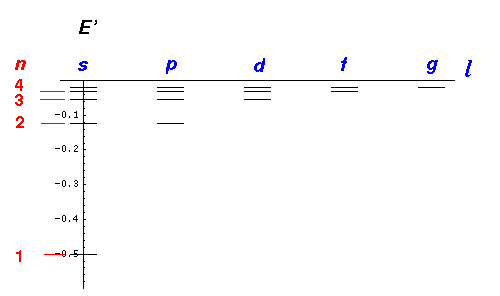
n	Included States	Total Degeneracy
1	1s	1
2	2s,2p	4=1+3
3	3s,3p,3d	9=1+3+5
4	4s,4p,4d,4f	16=1+3+5+7
5	5s,5p,5d,5f,5g	25=1+3+5+7+9

Note that atomic states are labeled by the principal quantum number n, thus there is no 1d state; the first d state is 3d.

Note that the degeneracy count of a particular (n,l) state described above [e.g., n=5, l=3 is 5f] is the result of the different values of m allowed with that l value: m may range in integer steps from -l to l, a total of 2l+1 possible values. Thus the degeneracy of the 5f state is listed as 7=2l+1 for l=3 in the equation: 25=1+3+5+7+9. The fact that the energy does not depend on m (the orientation of the angular momentum [classically the orbit's orientation in space]) but rather on l (the total amount of angular momentum) is the result of spherical symmetry.

The other piece of this degeneracy -- the fact that the energy depends on the sum of n_r and l through:
n = n_r + l +1
so 5s,5p,5d,5f,5g [i.e., (n_r,l)= (4,0), (3,1), (2,2), (1,3), (0,4) ] all have the same energy -- is a more complicated story. Here I simply mention the name: Lenz vector (a.k.a. Laplace-Runge-Lenz vector). This degeneracy means that there are five terms to add in the equation: 25=1+3+5+7+9

Next