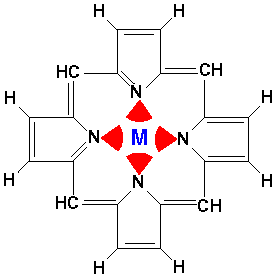
For example, consider the biologically important molecule porphyrin:

Porphyrin is a flat molecule that can act as a tetradentate (i.e., four nitrogen "teeth") chelating molecule for metals such as Mg, Fe, Zn, Ni, Co, Cu, and Ag (i.e., has "claw" that can grab and hold these metals). The red arcs represent the electrostatic interaction of the nitrogen's electrons. If the central metal is iron, the resulting iron porphyrin complex is the the heme group. There are four heme groups in hemoglobin in your blood. Heme is also the key part of enzymes like peroxidase, catalase, and cytochrome c. (In most heme compounds the iron picks up a top and a bottom atom producing a 6-coordinate, octahedral complex, rather than the square-planar 4-coordinate bare porphyrin.) A magnesium porphyrin complex is the heart of chlorophyll, the active molecule of photosynthesis.
Our aim in this section is to figure out the effect of the electrostatic cage on the energy levels of the central metal atom. We begin by considering a octahedral metal cage: 6 charges located at: r1=(h,0,0), r2=(-h,0,0); r3=(0,h,0), r4=(0,-h,0); and r5=(0,0,h), r6=(0,0,-h). We consider the electric potential field near the origin, which as usual can be expanded in Ylm. We use Mathematica for this task:
For small r:
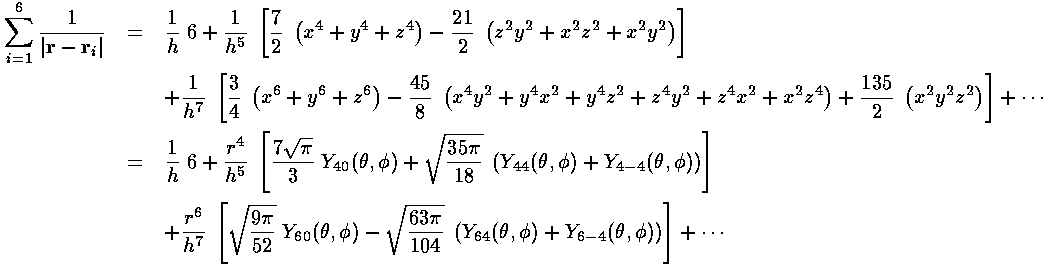
For large r:
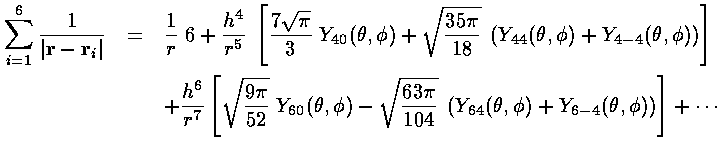
It is perhaps interesting to see how well this approximation works. (For our below calculation, a "good" approximation by the truncated series is not needed...all the [missing] higher terms produce zero result.)
Here is a set of exact isopotentials in the x-y plane:
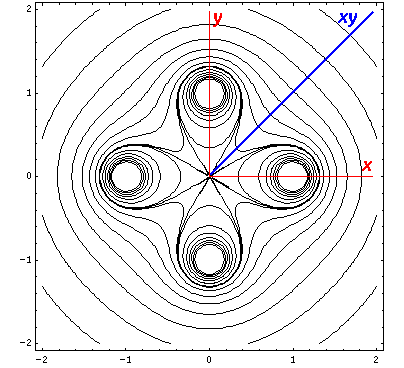
Contours are on the integer and half-integer values, except for the special contour at "6", for which I've provided additional contours at 6±.05
Of course by symmetry it looks exactly the same on the x-z plane, so instead we plot isopotentials for the plane that includes the z axis and the line x=y (which we call xy):
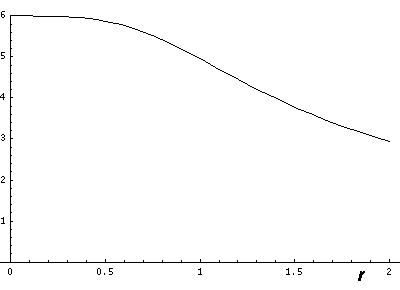
Now if we look at the potential and the approximate potential (in red) along the x=y=z (the "111" direction) there is no visible difference between the potential and the approximation. (In fact differences are less than 0.1.):
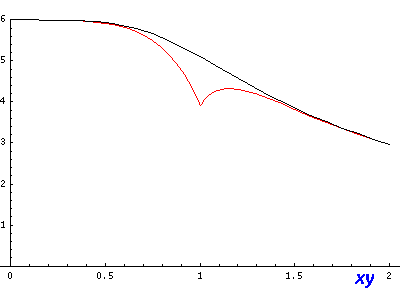
If we look (in the x-y plane) along the line x=y (and z=0) we can see a noticeable deviation between approximate (red) and exact (black) and a jump at r=1 in the approximate where we switch between formulas:
If we go right through on of the charges (e.g., by going along the x axis, the differences are large:
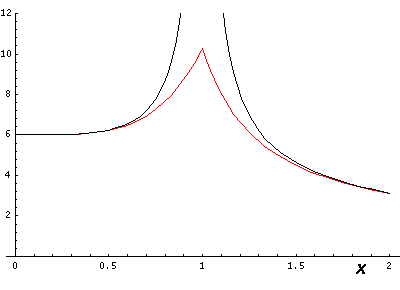
So lines that are far from charges are fairly accurate, but as you approach a charge the approximation breaks down, but only in a limited range (e.g., .5<r<1.5).
Here are our contours for our approximation for the electric potential:
Our game here is to see how the d orbitals are affected by the octahedral E field using first order (degenerate) perturbation theory. Thus we need to calculate the 5×5 interaction matrix involving the above electric potential and our 5 d orbitals (i.e., mi=2,1,0,-1,-2). We have typical terms like:
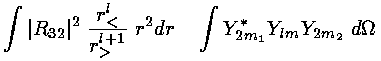
where r< is the smaller of r and h and r> is the larger of r and h.
From our previous results with 3-Y integrals:
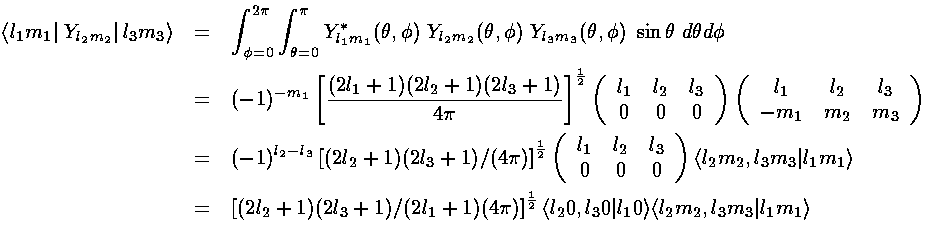
The l must satisfy the triangle inequality and add to an even number (so for us: l=0,2,4) and the m's must "add up": m1=m+m2. In this problem the smallest ls we found in our expansion are 0 and 4. The l=0 term (6/h & 6/r) must be diagonal. (Y00 is a constant that can be taken from the integral. From the above: non-zero integrals must have m1=m2; for those integrals normality tells us the result is 1. Since the result is independent of ms, it's a constant value down the diagonal.) Diagonal terms move all the d levels up or down together; they do not affect the level splitting which is what I'm aiming to calculate.
The three l=4 terms: Y40 and Y4±4, share the same radial integral, which becomes part of the multiplicative shift for all levels (much as the charge at the octahedral vertices is part of the overall scale factor). Y40 can't mix different ms, but it does have different values down the diagonal:
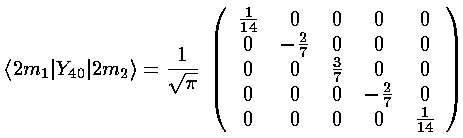
(Y4,+4+Y4,-4) mixes ms that differ by 4: m=-2 and m=2. The resulting matrix is:
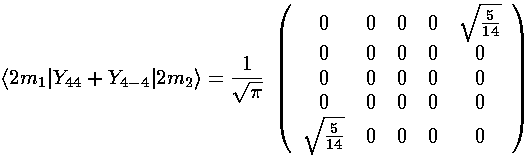
The interaction matrix (ignoring the overall factor of the radial integral and and overall shift up from the l=0 term) is:
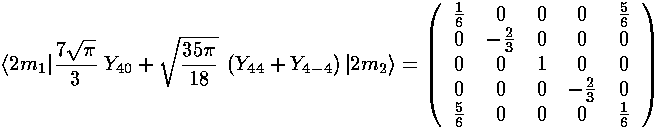
We can use Mathematica to find the Eigensystem (also easy to do by hand):
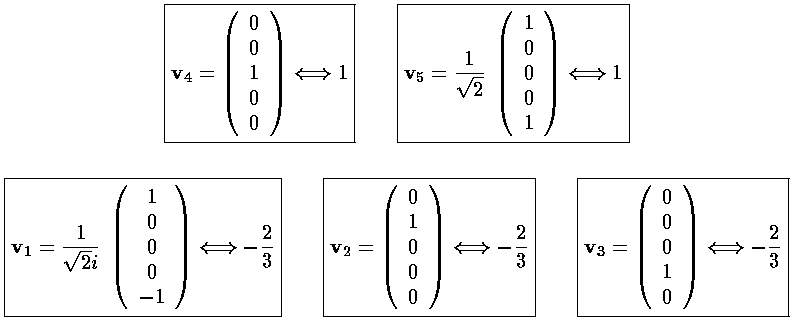
The result is that there are three degenerate lower lying states
("-2/3") and two degenerate higher states ("1"). The m=±2
have mixed. The mixed states lack  symmetry, so they
are harder to display. The lower lying state (v1, called by chemists
dxy) avoids the
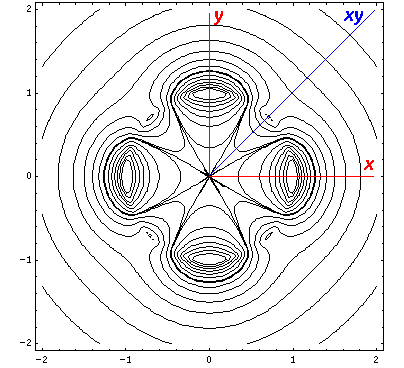
interaction by having its lobes point in the xy direction. Here is what
it looks like in the x-y plane:
symmetry, so they
are harder to display. The lower lying state (v1, called by chemists
dxy) avoids the
interaction by having its lobes point in the xy direction. Here is what
it looks like in the x-y plane:
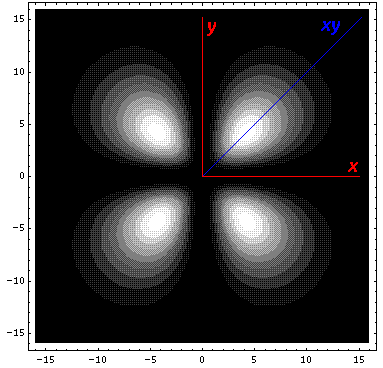
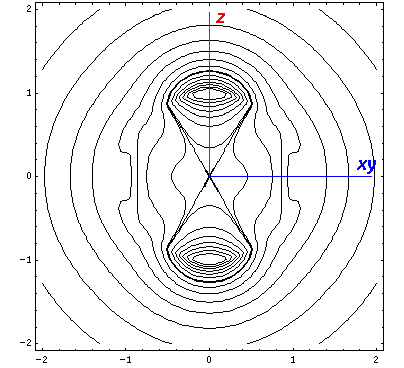
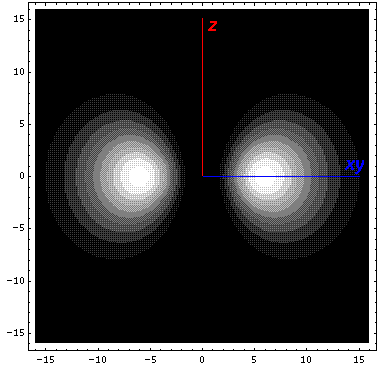
Here is what it looks like in the z-xy plane:
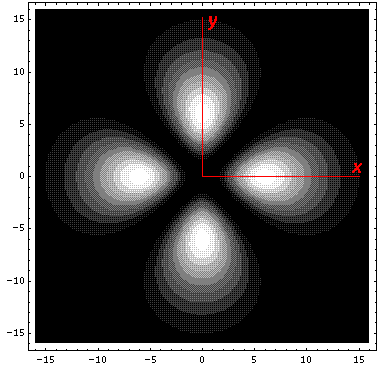
The higher lying state (v5, called by chemists dx2-y2) strongly feels the interaction because its lobes point at charges in the x and y directions. It is exactly like the above dxy orbital except rotated by 45°. Here is what it looks like in the x-y plane:
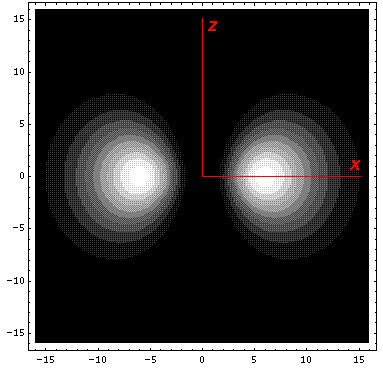
Here is what it looks like in the z-x plane:
The complex normalization [1/(2½i)] of v1
is designed to produce a real-valued function. In similar fashion one can make
linear combinations of the m=±1 states that are real-valued but lack
 symmetry. What chemists call dxz
is (-Y21+Y2-1)/2½. It's zero on
the x-y and z-y planes. We display it on the x-z
plane:
symmetry. What chemists call dxz
is (-Y21+Y2-1)/2½. It's zero on
the x-y and z-y planes. We display it on the x-z
plane:
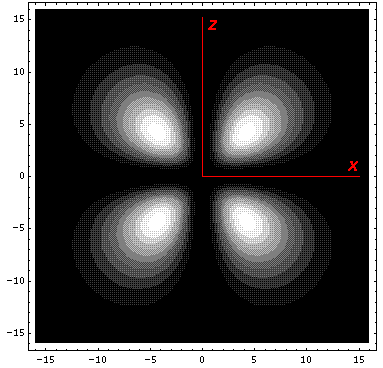
The other linear combination: (-Y21-Y2-1)/(2½i) called dyz is just like the above orbital, but rotated by 90°. (In fact the four orbitals: dx2-y2, dxy, dyz, dxz are identical except for orientation.) The Y2±1 orbitals are low lying ("-2/3") orbitals; as you can see they avoid pointing at the charges.
The amount of the splitting between these levels depends on the amount of the charge at the octahedron vertices. That of course depends on what molecule (called a ligand) is at those sites. Chemists have noticed a spectro-chemical series of ligands in which the energy jump gets increasingly large: (weak ligands) I-, Cl-, F-, OH-, H20, NH3, SO3-2, NO2-2, CN- (strong ligands).
One final example: ruby consists of a small amount of Cr+3 in an octahedral sites in a Al2O3 crystal. It's red color comes from the absorption of light by Cr+3 d electrons...Al2O3 has no color. The Al2O3 crystal plays the role of the ligands.