H-atom p.4

We now have a set of wavefunctions: = N ^l H()exp[-½] Y_lm or

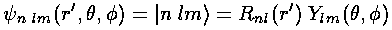These wavefunctions should be normalized:

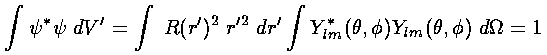Note: ^*= ||² (* means complex conjugate) is the probability density and the above integral is just the requirement that the total probability add up to one, i.e., the particle must be somewhere. Of course, the Y_lm are already normalized, so what remains to do is normalize R, i.e., make the r'²dr' integral of R² be 1.

The result is:

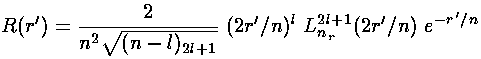
where we have used the normalization of the Laguerre polynomials:

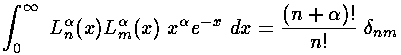
and the recursion of the Laguerre polynomials:

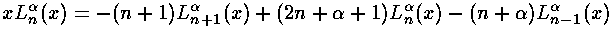
since the R integral has one-too-many factors of for immediate use of the Laguerre normalization integral (i.e., wavefunction orthogonality is not directly related to Laguerre polynomial orthogonality).

Quantum mechanics says that the particle does not have a position and that nature limits us to just reporting the probability of finding the particle in various locations. For each of the above possible energies there is a corresponding function describing where the particle is likely to be found: ||². I've usually used a "stacked wavefunction" plot to display the wavefunctions along with effective potential energy

V_eff=l(l+1)/(2r'²)-1/r'

But for the H-atom, the levels are not so uniformly spaced and the classically allowed range grows quickly with n (essentially like n²). Below I've displayed just the effective potential energy and the energy levels (from which you can see the classically allowed region) followed by the wavefunctions. Notice the that the x scale for the wavefunctions must change by nearly a factor of 2 between plots to fit the wavefunction in.

l=0 (s wave) for n=1,2,3,4

l=1 (p wave) for n=2,3,4

l=3 (f wave) for n=4

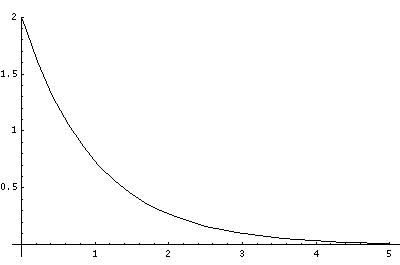
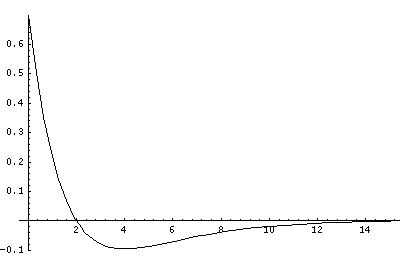
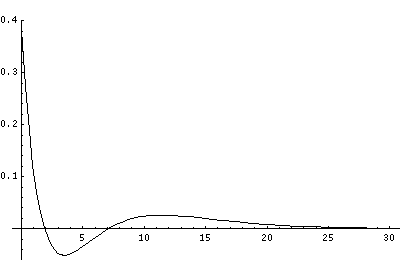
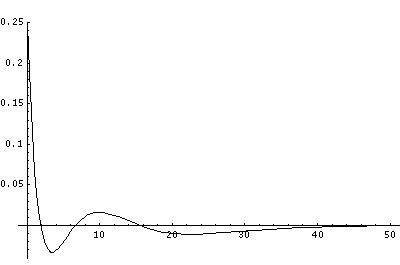
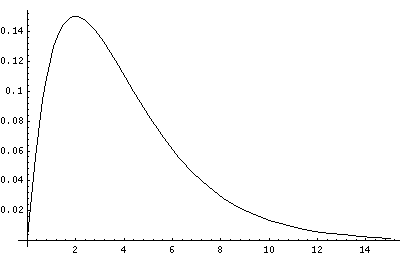
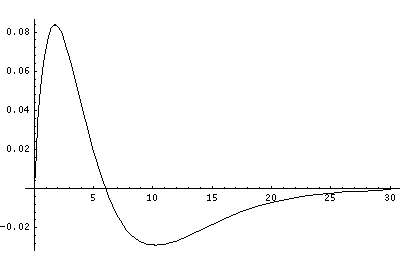
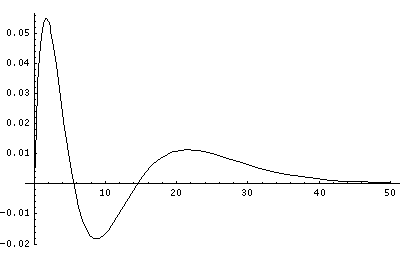
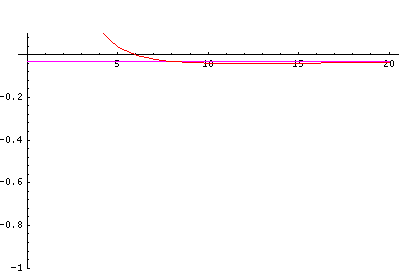
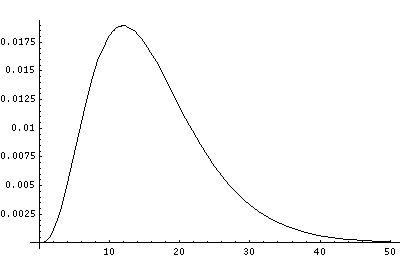
In order to make the wavefunctions look more WKB-like one often sees u=r'R(r') plotted. Here's an example of what that looks like:

l=10 (m wave) for n=30

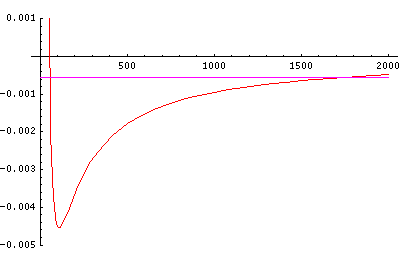
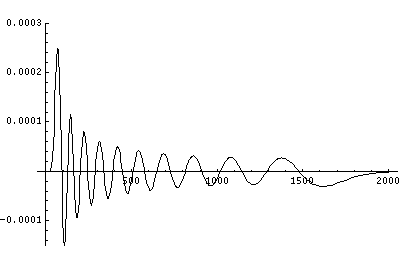
Now here's what u looks like:

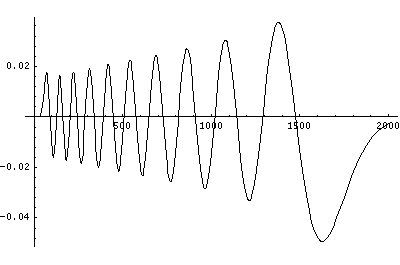
Note that with u you see the WKB behavior: as the kinetic energy gets small the wavelength lengthens and the u amplitude grows. Note the huge x-scale. Astronomers often observe H-atoms with n>100. Such atoms are "huge": about the size of a bacteria cell.