H-atom p.10

Stark Effect

The energy levels of atoms are observed by measuring the energy of the photons emitted as electrons make transitions between orbitals. Conservation of energy tells us that as an electron makes a transition from a higher energy orbital to a lower energy orbital, the energy lost by the electron ends up in the photon. (The energy of the photon is measured by measuring its wavelength or frequency.) Electrons in atoms can also absorb a photon if it provides exactly the right energy needed to propel the electron from its current orbital to a higher energy orbital. Thus if somehow we could increase or decrease the eigenenergies of an atom, we would observe changes in the wavelength (equivalently: frequency or color) of the photons of light produced or absorbed by the atom. It turns out that the energy levels are sensitive to the electric field in the vicinity of the atom. The shift in energy levels caused by an external electric field is called the Stark Effect.

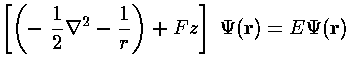
A particle with charge q in a uniform electric field E feels a constant force F=qE. If we assume the electric field is in the z direction and the particle is an electron with charge q=-e, the the force is in the minus z direction with magnitude F=eE, i.e., Fz=-F. The potential energy whose minus derivative produces that force is: Fz. In our dimensionless units, we have an interaction of F'z', where F=F'f. The unit f=B3/(2A)2 seems "small" (in an H-atom: 8.3×10-8 N), but it corresponds to an electric field of 5.2×1011 V/m, which is about a million times the largest field that can easily be produced in the lab. Thus the dimensionless force F' is a "small" number... say 10-6...so perturbation theory should work.

Neglecting to write the primes, our dimensionless Schrödinger's equation is:

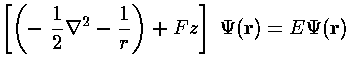
We now seek to find the energy shift due to the Fz perturbation on the unperturbed n=2 states (i.e., the four normal one-electron n=2 H-atom states: 2s and 2p). Since these states are degenerate, we must use degenerate perturbation theory and calculate the 4×4 matrix: <i|Fz|j> where i,j run over the four states: 2p [m=-1,0,1] and 2s. This process is made easier by recognizing that z=r cos = [(4)/3]½rY10. Thus we can use our earlier result on 3-Y integrals:

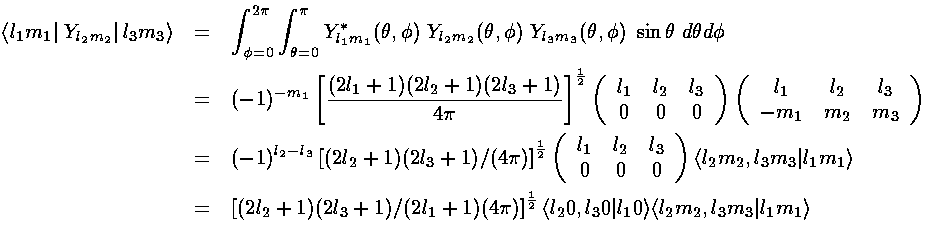
These integrals are zero unless the m's "add up": i.e., m1=m2+m3. In our case "m2" is zero so the only non-zero integrals will have m1=m3. (Our perturbation maintains symmetry and so it does not mix states with different m.) Additionally we've noted:

Under inversion, Ylm(-1)lYlm. The integrand must be overall even to produce a non-zero result, hence: l1+l2+l3 must be even.
For us l2=1, so the only way to avoid a zero integral is to have l1+l3 be odd. Thus the only non-zero matrix element is the one that mixes 2p(m=0) and 2s. The angular part of that integral is easy because it involves a Y00 which is a constant [1/(4)½] and hence can be pulled from the integral. The radial integral can be done with Mathematica.

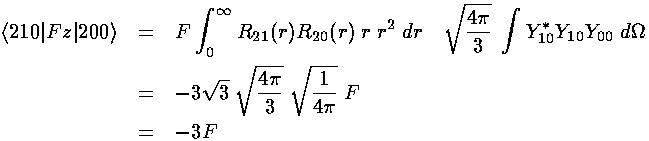
The resulting matrix of mixed states:

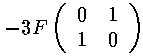
With eigenvectors and eigenvalues:

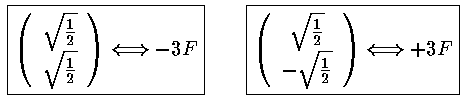
The m=±1 states have zero matrix elements for all states, so they remain unshifted in the first-order approximation. Thus of the four degenerate states, one [(|200>-|210>)/2½] has moved to higher energy with a shift of +3F, one [(|200>+|210>)/2½] has moved to lower energy with a shift of -3F, the other two have zero shift.

It is informative to look at the shifted Stark states. The new wavefunctions are linear combinations of the initial wavefunctions (|200>±|210>)/2½. (Chemists call linear combinations of orbitals hybridized orbitals. This particular pair are called sp hybridized orbitals. We'll soon learn about sp2 and sp3 hybridized orbitals.) These hybridized orbitals "reach out" to regions of high and low potential. (In the below contour plots the region near the nucleus has been "over exposed" in order to show more of the outward-reaching lobe.)

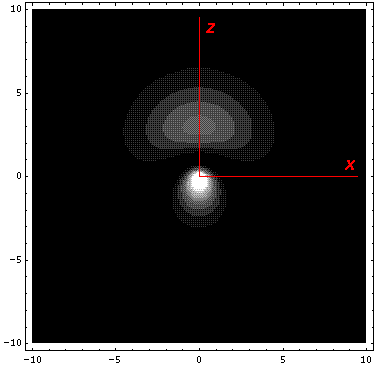
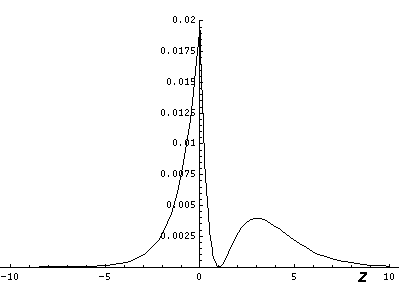
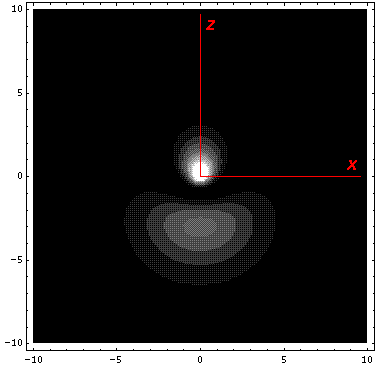
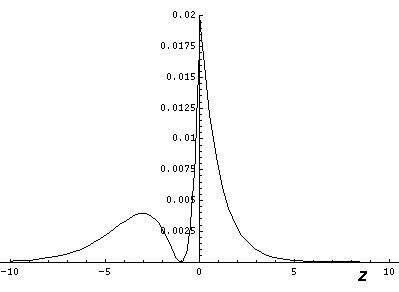
High energy state: reaching up to higher potential

Low energy state: reaching down to negative potential

Nature is performing a giant experiment for us in the sky. Light of all colors is produced in a star's core and must work its way through the largely hydrogen stellar atmosphere before it reaches us. Thus certain colors of light will be absorbed by the star's atmosphere (and hence show up as depleted as viewed from Earth). The particular wavelengths (colors) absorbed are determined by the energy jumps that electrons might make in the atoms making up the atmosphere of the star. Now if the atoms in the atmosphere of stars were isolated, so for example, no neighboring ion is producing a perturbing electric field to stark-shift the energy levels, the possible energy jumps would be the same...all the absorption would occur at exactly the same wavelength. On the other hand, if the atoms were in a dense atmosphere, with neighboring ions and varying electric fields, the energy levels would have slight shifts and some atoms would have larger energy jumps others smaller. As a result the light would be depleted at a (small) range of wavelengths. The larger the density of the atmosphere, the larger the perturbing electric fields from neighboring ions, the larger the range of absorbed wavelengths (the larger the "width" of the absorption "line"). Thus by looking at the line widths of the absorbed light from stars we can determine the density of the gas in the star's atmosphere. Some stars have a huge radius....they are much expanded versions of the Sun. Naturally they have low-density (rarefied) atmospheres. Stars like the Sun (called "dwarfs" or "main sequence stars") have relatively wide absorption lines.

While the atmosphere's of stars are largely made of hydrogen, most often essentially all elements are present, just in low concentration. Of course if the atom is rare in the atmosphere, its characteristic energy jumps (with corresponding wavelengths of absorption) are only slightly depleted in the light making it through the atmosphere of the star. Nevertheless, one can see the same sort of density effect with elements other than hydrogen in stars. Strikingly the effect, while present, is much smaller in other elements than it is in hydrogen. Why?

Note that if we were to ignore the l degeneracy in hydrogen, we would have calculated the first-order shift by finding the expectation value the the perturbation e.g.,

<2s|Fz|2s>

All such expectation values are zero! Thus the energy shift would be second order (F2; and remember F is something like 10-6) and hence much smaller. Because of l-tilting atoms other than hydrogen are non-degenerate, and hence have much smaller stark shifts. The large widths of hydrogen absorption lines in dwarf stars is due, in part, to the l-degeneracy of the H-atom.

Imagine for a moment the problem of determining the Stark shifts for the n=3 H-atom. By our previous work only states with the same m would mix. Thus we'd concern ourselves with the three m=0 states: 3s, 3p, 3d; the two m=±1 states: 3p, 3d; the lone m=±2 must be unperturbed. The 3-Y matrix element would allow mixing of s&p and p&d only. We would end up needing to do the following integrals:

<300|Fz|310> <310|Fz|320>

<311|Fz|321>

and then find the eigenvectors of the 2×2 and 3×3 matrix.

A simpler approach is available via a change of coordinates. With the Fz perturbation, our Hamiltonian is no longer spherically symmetric; it now has only -symmetry. It turns out there is a better choice of coordinates than spherical: parabolic.

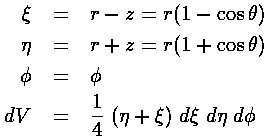
The H-atom Schödinger's equation separates in these coordinates, the resulting wavefunctions are:

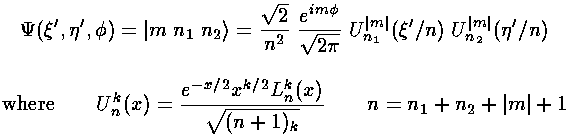
The only non-zero matrix elements of the z perturbation are diagonal:

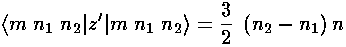
showing that the eigenenergies are evenly spaced. The below shows the display of eigenenergies for n=5

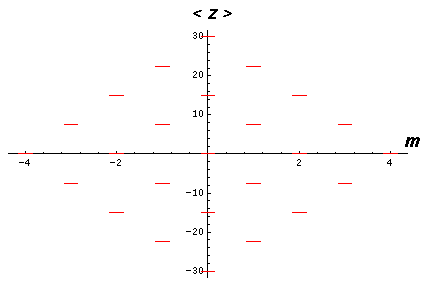
The even spacing suggests a harmonic oscillation. Indeed semi-classically what is happening is that the elliptic orbit is oscillating about the direction of the electric field. When the major axis of the orbit is aligned with the E, the angular momentum is maximized. When the major axis has reached its maximum deviation from E, the angular momentum is minimized. The orbit is "wagging its tail" in the direction of E while the z component of the Lenz vector remains constant.

Classically the Earth feels the Sun's gravitational potential plus a perturbing potential from the Galaxy. Is the Galaxy's perturbing tidal force on the Earth enough to reduce the eccentricity of the Earth's orbit and send it crashing into the Sun?

Next