We have already studied the bound states in such a potential. We then used a shifted energy origin so that the potential was zero at the bottom of the well. Here we take the the top of the well to be U=0. This is the same strategy we adopted in 1d when we studied bound states in finite square wells and then scattering from finite square wells.
This problem is very similar to the equivalent 2D problem. You should review that material before proceeding, as I will very much limit here the discussion of such of interesting effects as rainbows and resonance as they are exactly analogous to the 2D case.
As we have seen, classically
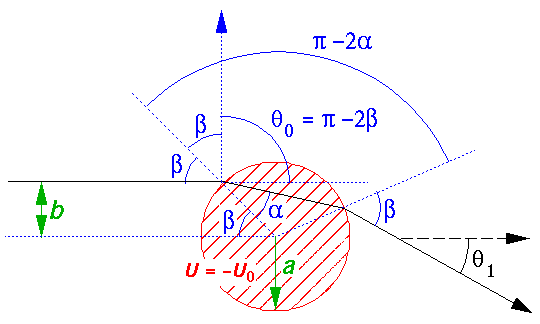
the effect of entering a region with U=-U0
is much like refraction. The component of velocity parallel to the
interface's normal is increased (as required by conservation of energy) while
the component of velocity parallel to the interface is
unchanged (as there is no force in that direction). The angle of
incidence (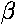
) and the angle of refraction
(
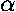) end up related as in Snell's Law:
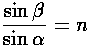
We seek to relate the impact parameter (b) to the
scattering angle (
). The development
is identical to that in the 2D case, except drawings like the
top one are made in the scattering plane. Again, I direct your
attention to our previous work.
While classically (and even in the WKB approximation) there is no reflection, we know from our previous work that reflection will accompany refraction in quantum mechanics. Thus we can have immediate reflection or we can have one or more reflections inside the potential well. That is to say the path of the "particle" may include N=0,1,2,... internal chords. The net result of an N internal chords, is to rotate the exit normal from the entrance normal by:
N(
-2)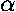
Thus, we have the relationship between the scattering angle and the impact parameter:
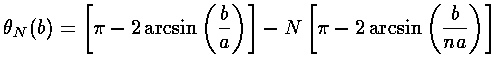
We plot some of these results in the cases n=1.5 [red], 1.6 [orange], 1.7 [green], 1.8 [cyan], 1.9 [blue], 2.0 [violet].
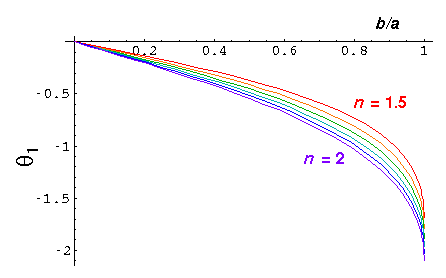
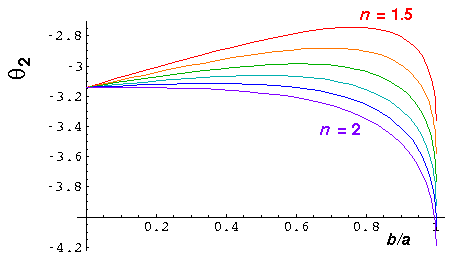
Note in particular the curves for N=2. We see that the scattering angle has a maximum at an angle a bit more than -180° and thus a rainbow [old news]. However there is some new behavior: in the range n between 2½ and 2, we have scattering to the angle -180° for non-zero b...a backscattering glory. Here's what the scattering looks like for n=1.75:
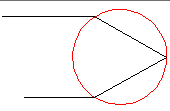
Note however, that the rainbow angle is quite close to 180° so it is hard to tell the glory from the rainbow.
In making the connection between particles and QM, note that
n is a strong function of energy. Thus at low energy
n is large and reflection becomes quite likely; whereas at high energy
n
1 and the cross-section declines.
In quantum mechanics we proceed much as on the previous page. Outside the well we have solutions of the form:
jl(k'r') Ylm(,
) and
yl(k'r') Ylm(,)
where E'=k'2. We choose to write our solution a as sum of spherical Hankel functions:
[hl(2)(k'r') +
exp(2i
l)
hl(1)(k'r') ] Ylm
Inside the well the solution must be regular at the origin and hence a j:
jl(q'r') Ylm
where E'+U0'=q'2 (i.e., the particle has more momentum when inside the well).
Our job is to match the logarithmic derivative
(
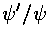) at the well boundary (r'=1). Thus:
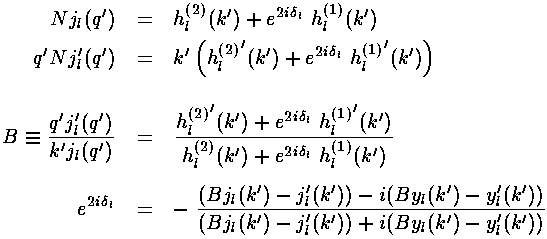
Consider the previously worked case of U0'=50. Recall that we had two bound states for l=0 and 1, and one bound state for l=2-4, and no other bound states for larger l. We plot below the phase shifts (l=0-5) for this problem as function of particle momentum k':
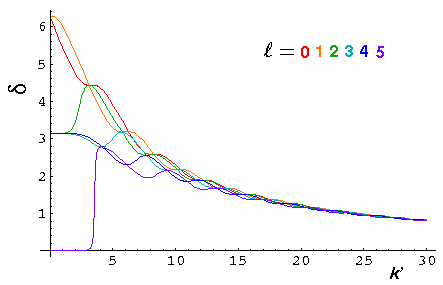
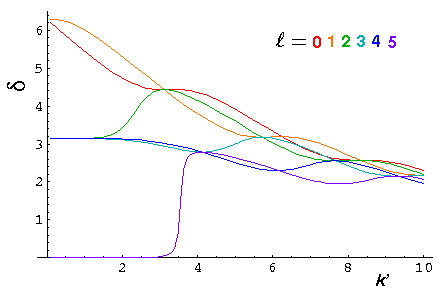
The phase shifts are positive for this attractive potential whereas they were negative for the reflecting (repulsive) potential.
Note that at high energy, all phase shifts approach the same value, which as given in the WKB approximation is:
=½U0'/k'
Note that at low energy, all the phase shifts, approach a multiple of
, which means the same as =0:
no scattering. If |B| is large (as it usually is at low energy
[small k']) the above phase-shift formula reduces to the phase shift formula for
the fully reflective well. Thus, exactly as on the previous page,
we expect the mth phase shift to go to "0" like
k'2l+1. The k'=0 value of
the phase shift is j, where
j is the number of bound states with that value
of l. (The highest energy bound state has "sucked in"
j of phase [e.g., it has
j-1 nodes]. Higher energy states [e.g., E=0]
start with this phase which is reduced at high energy
(where n1) to zero.)
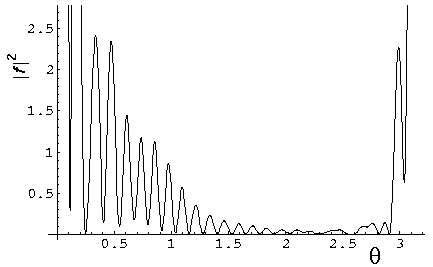
Here are plots of the differential cross-section at k'=.1, .3, 1, 3, and
10. Note we progress from a large uniform cross-section at low energy,
to a cross-section that is small for moderate ,
with a strong a strong diffraction/refraction peak near =0.
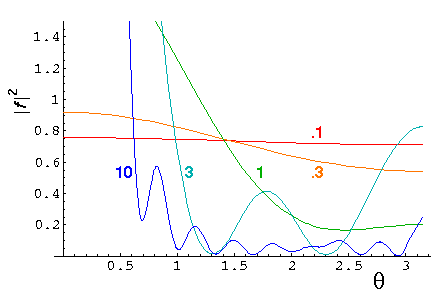
It is helpful to define the total cross-section:
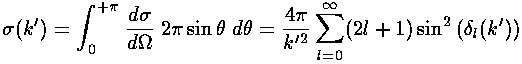
The total cross-section is related to the fraction of the particles experiencing any scattering in the sample. We plot below the total cross-section as a function of k'
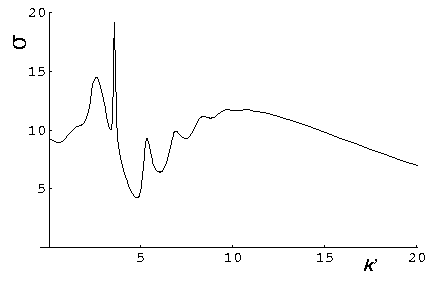
Note the sharp peak (resonance) near k'=3.5 (and weaker peaks at 5.5, 7, ... and 2.5). Notice that the l=5 phase shift reaches maximum scattering (90°) near k'=3.5. These are examples of resonance, exactly as discussed in the 2D case.
Here are some plots of the probability density for our U0'=50 potential. First at k'=10:
.
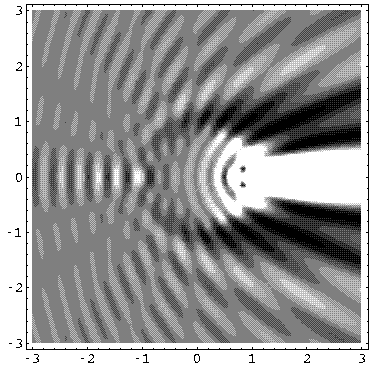Here is a plot of the probability density along the z axis:
.
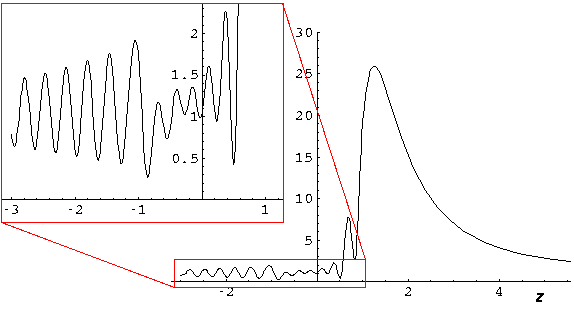The huge peak at z near 2 is a result of focusing as shown in the below ray diagram:
.
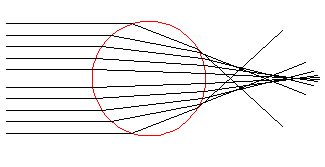In the case of k'=1, the equivalent index of refraction n is over 7, so (1) reflection rather than refraction is common and (2) refraction does not produce a focus outside of the sphere:
.
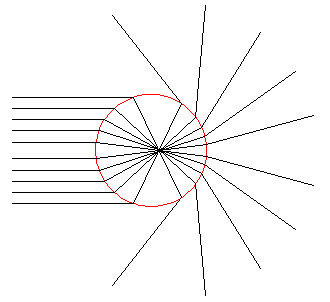Here is a plot of the probability density along the z axis for k'=1
.
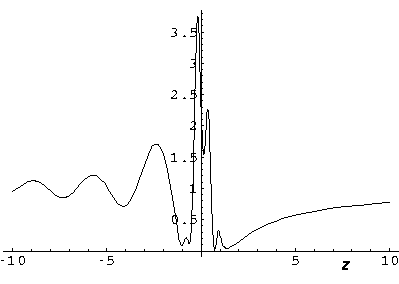Here is the corresponding probability density plot:
.
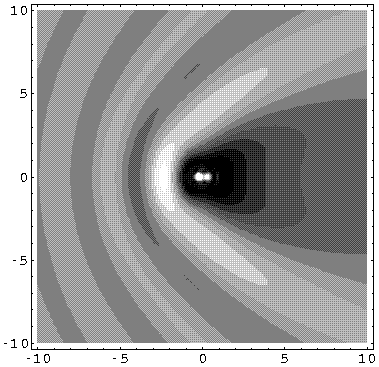Finally, here is a set of cross-sections with k'=30 but with U0' also increased so that n=1.75. Note the main N=1 pure refraction peak, and the much smaller backscattering glory:
