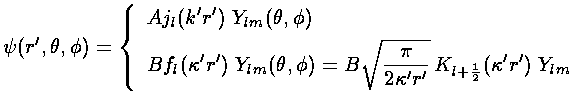
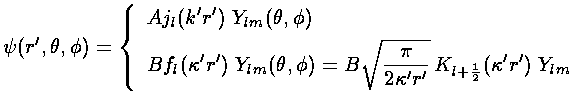
where, as previously,
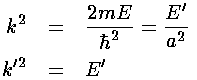
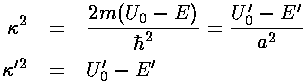
These two solutions need to match up
at the well boundary; we require both 
and
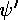to be continuous at r=a.
(The second derivative of
will have a step at r=a to match the step in potential as
required by Schrödinger's equation.) As before dividing the
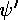-match equation by the -match equation
(i.e., matching the logarithmic derivative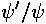 
) eliminates
the unknown normalization constants:
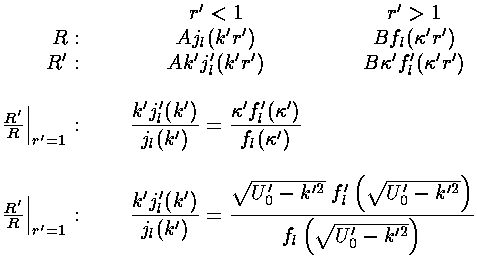
The 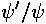equation is a nonlinear equation
for the unknown k' given the size of the potential step: U0'.
Clearly 0<k'<(U0')½.
We examine the nature of the solutions by displaying the right hand side of the
equation in blue and the left hand side in red. Solutions are where the two curves
cross.
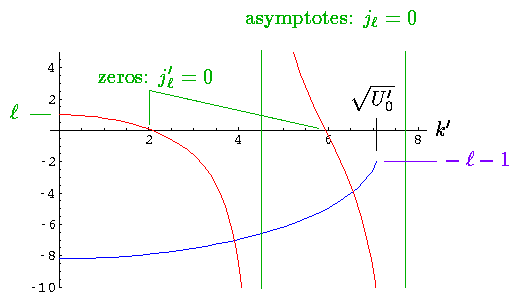
The lhs (red) starts (k'=0) with y value l; it crosses
the x-axis at the zeros of jl' and reaches
±
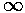asymptotically at the zeros of jl.
The rhs (blue) is always negative since the fl(x) have negative
slope; in fact, since for large x
fl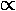(x) 
e-x
so fl'/fl should be approximately -1. Thus
the rhs should start at nearly -(U0')½. It ends
at k'=(U0')½ with a y value
of -l-1. [The above plot is for l=1 and U0'=50
and shows two solutions. The wavefunctions are displayed below.] Clearly there will
typically be an intersection for k' between a zero of jl'
and a zero of jl. Unlike the lower dimensional square wells,
there is not always a solution (i.e., a weak 3d well may have no bound states
even though it's slightly attractive). We would just barely have a l=0 solution if
the lhs reached -1 at k'=(U0')½.
This will happen if U0' > 
2/4.
[Mathematically the l=0 state is identical to the first excited state of
the 1d square well...see the (
R) differential equation
and note the boundary condition that (R)=0 at r'=0.)
Once the magic value of k' is found, the following wavefunction
has continuous and .
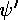The constant A is determined by normalizing the wavefunction.
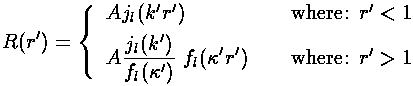
Here are some resulting wavefunction for U0'=50.
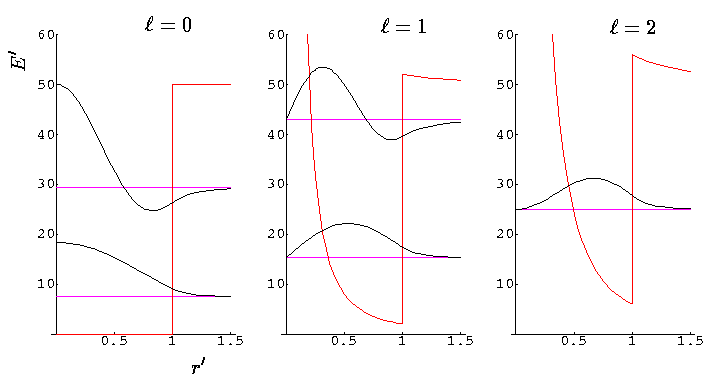
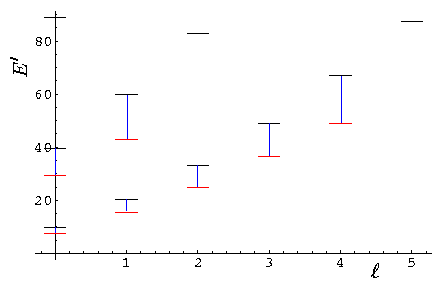
Here is a display of the energy levels:
In the low lying SHO states we would find much the same pattern, except we would have degeneracy between the second s state and the first d state and between the second p state and the first f state. Here we see "l-droop", the large l states in the SHO degenerate multiplet have drooped below the other states in the multiplet.
Below is a plot comparing the infinite square well energies with those of the U0'=50 system (each infinite square well energy [in black] is connected by a blue line to the equivalent finite square well energy [in red]).
