- Another famous formula involving the Dirac delta function is:
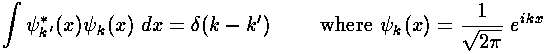
Describe how the units work out in this equation. Give a qualitative
discussion as to why this integral is zero unless k=k'
(in which case it's infinite).
- A narrow, deep square well should approximate a delta function.
Show how our square well solutions go over to our delta function
solution in the limit of a deep, narrow well.
- For scattering from a "one-nuclei" delta function, we
found
the reflection amplitude:
R = -1/(1+ik)
For a square well potential we found
the reflection amplitude to be:
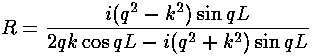
Now a narrow, deep square well should approximate a delta function.
Show that in this limit the above two formulae agree.
- Consider a variational approximation to solving the
"one-nuclei" bound state problem. Try a gaussian trial wavefunction:
 = exp(-ax2)
= exp(-ax2)
with the adjustable parameter a. Try another function
of your own choosing.
- Use the graphs
a = s(tanh(s)+1)
a = s(coth(s)+1)
on page 4 to estimate the bound state
energies for a diatomic molecule a=1,2,3,4. Find those energies directly with a root
finder. How do the two methods compare?
- We worked out the quantum mechanical motion of the N=8
molecule. The two state (say a=4) molecule has quite
interesting "motion"...work it out. What is the period? Can you relate
the period to quantum mechanical variables?
- Write down the order of the lowest four H2+ energy
levels for a=10. What are the next three levels?
- The fourth state on your list should be:
 u. Describe why, under inversion
between the nuclei, the label "u" is deserved. Describe this state!
u. Describe why, under inversion
between the nuclei, the label "u" is deserved. Describe this state!
- Earlier
we have worked out the energy levels of a 2D infinite circular square well.
It is trivial to extend this model to a cylinder. Find the aspect
ratio (length/radius) of a cylinder which produces the same ordering
of states.
- Consider the aufbau of N2, O2, and F2.
Show how the electrons are distributed for N2. I claim
O2 has unpaired electrons. What does that say about the
state beyond that used for N2?
Show how the electrons are distributed for F2.
- Approximate the ground state energy of a H2+
molecule by the variational method. Use as your trial function:
exp(-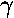 r1) +
exp(-
r1) +
exp(-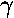 r2)
r2)
where r1 is the distance from one nuclei and
r2 is the distance from the other. Plot the results
as a function of a and compare to the exact result displayed on
page 4.
- Approximate the energy of the first
 u
orbital energy by the variational method. Use the above wavefunction multiplied
by:
u
orbital energy by the variational method. Use the above wavefunction multiplied
by:
exp(i )
)
What is the justification for using the variational method to find
an excited state energy? Plot the results
as a function of a and compare to the exact result displayed on
page 4.
- Consider the simple 1D molecule with repulsion:
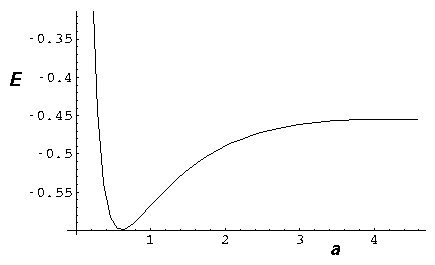
Find the "spring constant" that defines the motion near
equilibrium. Assume the nuclei weigh 2000 times the elections.
Find the frequency of oscillation in our dimensionless units.
Don't forget reduced mass, and be careful working out the units!
- Consider the real H2 molecule:
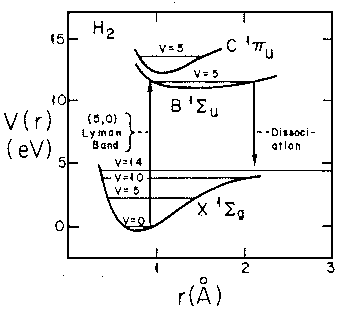
Find the "spring constant" that defines the motion near
equilibrium. Assume the nuclei are protons.
Find the frequency of oscillation in Hz.
Don't forget reduced mass, and be careful working out the units!
- Consider the theoretical H2+ molecule:
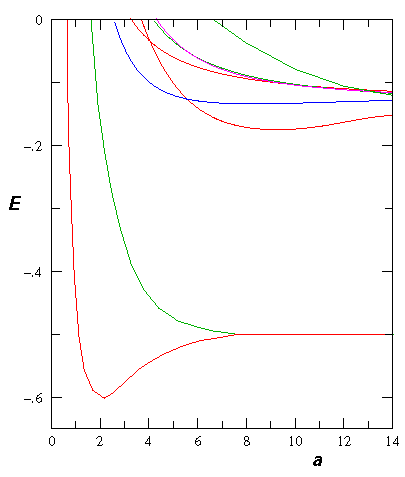
Find the "spring constant" that defines the motion near
equilibrium. Assume the nuclei are protons.
Find the frequency of oscillation in Hz.
Don't forget reduced mass, and be careful working out the units!
- on page 5 I claim the N=3
molecule looses levels at a=3/2 and 1/2. Show this.
- We separated the bands from the gaps on the basis of the
magnitude of the eigenvalues: in the bands, where the wavefunction
oscillates, |
 |=1
where as in the gaps, where we have decay or growth, we have
one eigenvalue |
|=1
where as in the gaps, where we have decay or growth, we have
one eigenvalue | |>1. The ability to make this
separation was bases on the determinant of [M] being 1.
For general potentials separated by free regions, show:
|>1. The ability to make this
separation was bases on the determinant of [M] being 1.
For general potentials separated by free regions, show:
| det([M]) | = 1
- Find [M] in the case of a nuclear potential given
by a finite depth square well. Find the band structure for some
particular well.
- Consider a lattice where we double the cell size by moving
every other nucleus to the left by some distance b:
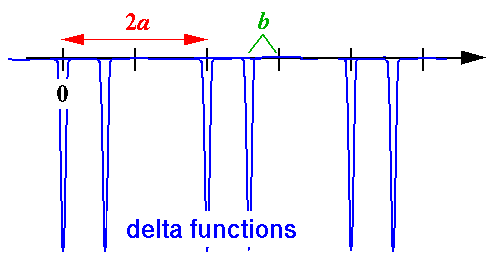
Find the band structure.
- In the band structure pages, I stress
the usefulness of studying a empty (free) lattice. Find the band structure
of an empty 1D crystal, and compare to that we found with delta function
nuclei.
- Find the band structure of a lattice of repulsive (+
 )
potentials.
)
potentials.
- Consider a particle in an infinite square well with a repulsive delta
function at its center. Find the exact eigenenergies. Find the
approximate eigenenergies by treating the delta function as a perturbation.
For the ground state, calculate and numerically sum the second order
perturbation contribution. Plot the results as a function of the
strength of the delta function.
- Consider the N=3 molecule with a=2. Using the
below plot (or direct calculation) find the eigenenergies of the
three levels. Find a finite square well whose energy level
ratios approximate those found in the delta function case.
Discuss the difficulty of doing the same thing for a=4.
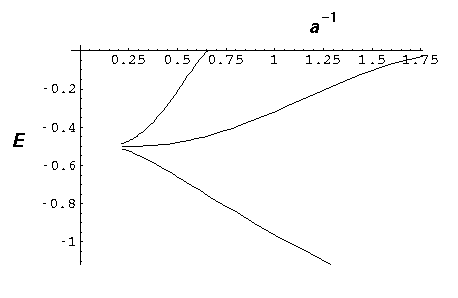
- Investigate the spacing of the finite molecule energy levels
within the energy band. Consider, for example, N=16, a=4
molecule. Find all its eigenenergies and plot the results on the
band. Find the q that correspond to each energy level.
- Consider a case like a=½ where the band spans
E=0. Combine the E<0 band with the
E>0 band into one plot.
- Consider two adjacent bands accessible to scattering.
One has negative group velocity and the other has positive group velocity.
Using a relatively large crystal for example, N=32, create
a superposition solution in which a lump of probability approaches
the crystal with (a) energy in the negative group velocity band and
(b) energy in the positive group velocity band. Describe the quantum motion
in each case.
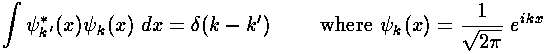
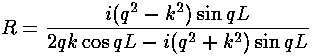
 = exp(-ax2)
= exp(-ax2)
 u. Describe why, under inversion
between the nuclei, the label "u" is deserved. Describe this state!
u. Describe why, under inversion
between the nuclei, the label "u" is deserved. Describe this state!
 r1) +
exp(-
r1) +
exp(-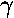 r2)
r2)
 u
orbital energy by the variational method. Use the above wavefunction multiplied
by:
u
orbital energy by the variational method. Use the above wavefunction multiplied
by:
 )
)



 |=1
where as in the gaps, where we have decay or growth, we have
one eigenvalue |
|=1
where as in the gaps, where we have decay or growth, we have
one eigenvalue | |>1. The ability to make this
separation was bases on the determinant of [M] being 1.
For general potentials separated by free regions, show:
|>1. The ability to make this
separation was bases on the determinant of [M] being 1.
For general potentials separated by free regions, show:

 )
potentials.
)
potentials.
