Delta Function Potentials p.8

Quantum Motion

Consider again our a=4, N=8 molecule whose wavefunctions were displayed on page 5. Recall that the every wavefunction sampled the entire molecule: the electron was not associated with any particular nucleus. What would happen if we released an electron on a particular (say the end) nucleus?

As soon as we start talking about time dependence, we must give up single energy eigenfunctions: they are stationary states with probability densities that do not change in time. Instead to have motion we must be in multiple eigenfunctions; the precise nature of the linear combination is determined by the initial state.

Thus let's consider an electron "attached" to the first nucleus. Of course to localize the electron to exactly x=0 would require infinite energy. Thus we let our initial condition be the same as that of an electron attached to a solitary nucleus (=1):

initial = f(x) = exp(-|x|)

We start by using our wavefunction orthonormality:

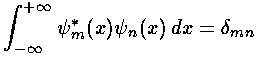
to extract the coefficients b_n necessary to write our initial state in terms of energy eigenfunctions.

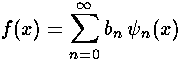
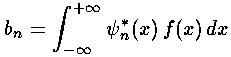
Note that each single energy eigenfunction has simple (but individualized) time dependence:

exp(-i E_nt)

When we let our linear combination evolve in time, the linear combination changes, that is to say, f changes and the electron moves.

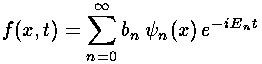
We make our life easier by restricting our sum to just the finite number (8) of bound states: we choose not to include the infinite collection of unbound wavefunctions. (The parts of a initial state that includes unbound wavefunctions, is itself unbound and will soon leave the area anyway.) We simply do the 8 integrals, express our initial state as a linear combination of those 8 states, and then let time evolve.

The result is that our electron moves away from its initial nucleus with a velocity of a bit more than .1. (I find x=12, t=100.) Here are some snapshots along the way:

t=0

t=50

t=100

t=150

t=200

t=250

t=300

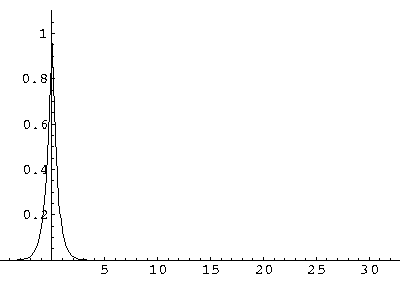
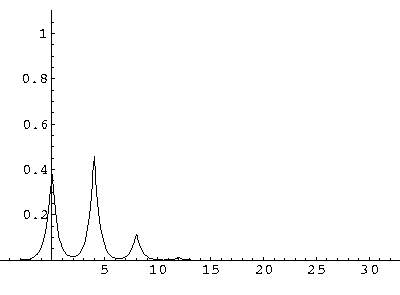
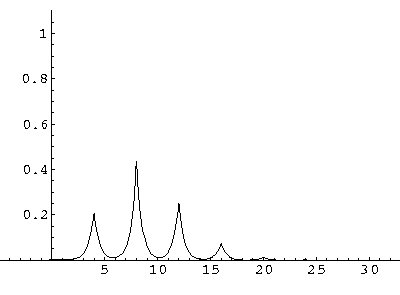
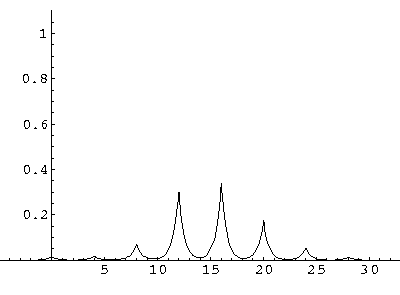
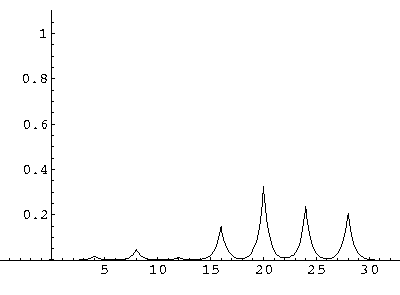
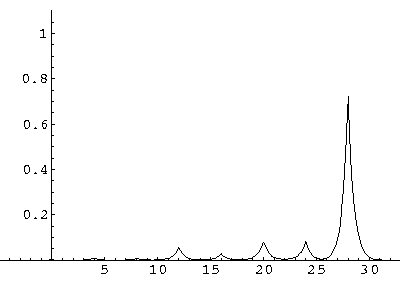
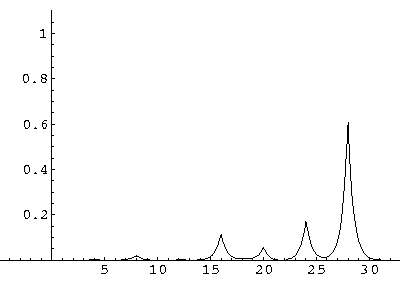
For .27 Mb you can watch a QuickTime movie of this motion.

The organization of this motion is a bit surprising: you are watching tunneling between adjacent wells, but it is tunneling that maintains direction; it is not a random walk. Since the eigenenergies are not evenly spaced the motion is not periodic, and eventually we expect an apparently random (but still time dependent) state. Indeed after about 5 "cycles" no obvious coherent motion is evident.

How do we explain this result? If we take seriously our band results (E(q)), we can find the group velocity by taking the derivative:

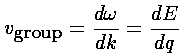
If we plot up the group velocity as a function of E for the first band we find:

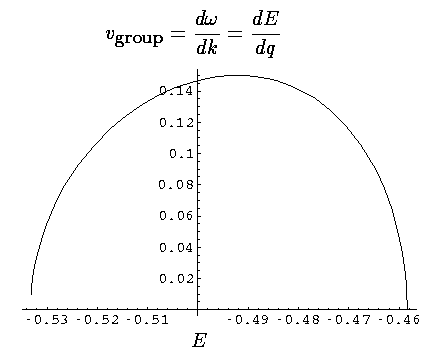
Now our moving electron is a superposition of 8 energies, but the average energy is essentially -.5. Thus our observed velocity makes sense.

Finally note that narrow bands necessarily have small slopes (w.r.t. q), and hence have slow moving excitations.