Delta Function Potentials p.5

Three or more Attractive Delta Functions: Bound States

OK, two delta function "atoms", gives us a delta function molecule "H₂". Does three delta function "atoms", give us "H₃"? Folks whose prejudice is based on the upper right corner of the periodic table (where: N₂, O₂, F₂, Cl₂, Br₂, I₂ live) expect no further bonding; folks who know that most elements are metals expect atoms to continue to line up until we've formed a small crystal: say, 10²³ nuclei each separated by, say, 1Å. Instead of first building the machinery to solve the many "nuclei" problem, let's jump to the results.

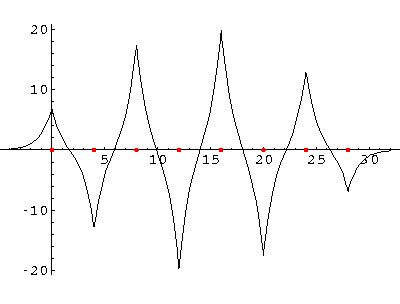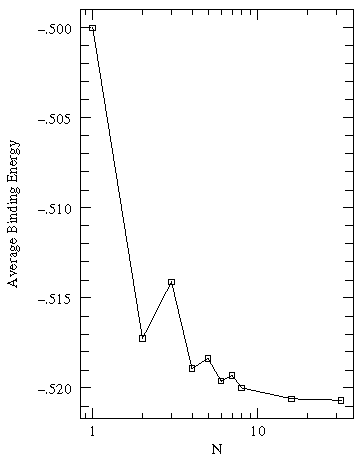
We can solve for the energy eigenvalues for three delta functions each separated by a. Here are the results:

On the lhs (large a, strong potentials, little wavefunction overlap) we have 3 nearly degenerate energies near the isolated well energy of -½. On the rhs (small a, weak potentials, large wavefunction overlap) we see those levels separate. for a=3/2 we loose one, for a=1/2 we loose the other. For zero a we have a unified well with a single bound state: E=-9/2

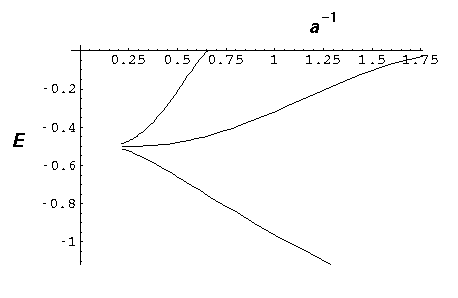
Now add a fourth "nucleus":

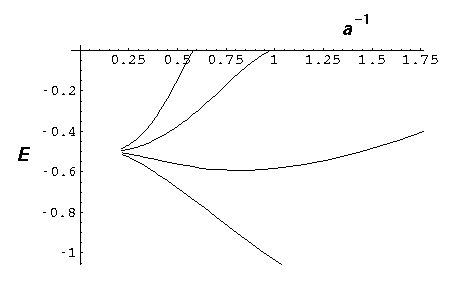
Now double that to 8 "nuclei":

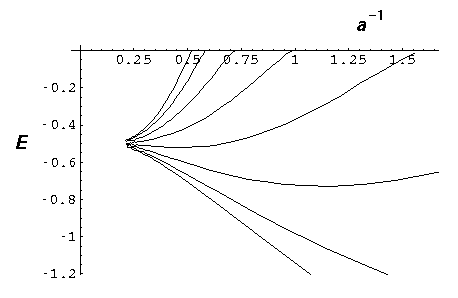
We now focus on just the energy levels for a=4 and vary the number of atoms: N=8,16,32:

Notice that as we add more atoms, we do not affect the range of allowed energy; instead we just produce more states within the same energy band. If we had N nuclei, we'd have N states in the band. Notice that within this energy band the density of states is not uniform: there are more states per energy bin at the bottom and top of the band than in the middle.

Wavefunctions

What do these "molecules" look like?

The most important point is that all of the wavefunctions are spread over all of the atoms. There is no localized chemical bond between just two atoms--every wavefunction samples the entire molecule. Approximately speaking the wavefunctions look like the symmetric sum of the solitary wavefunctions amplitude modulated (i.e., multiplied) by harmonics of a sine wave that fits the molecule. Here are the wavefunctions for N=8, with the ground state presented first. (The red dots are the delta functions.)

Binding Energy

Consider the case of assembling a molecule of N nuclei and N electrons. If N is odd, one electron must be unpaired, but generally we'll pair electrons in the lowest available state, thus half-filling the band. Since the lower half of the band is below E=-½, an average electron will have an energy of less than -½, i.e., less than in a free atom. Since the band energies remain fixed as more states go into the band, the average binding energy of an electron soon reaches a constant value. Below we plot these results for the case a=4.