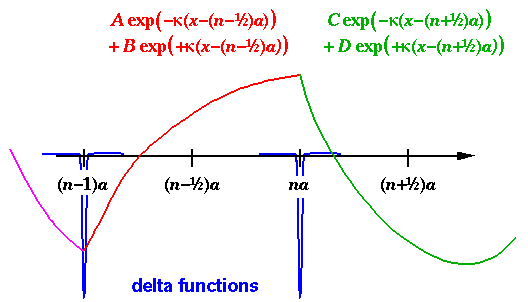
A series of attractive delta functions are located at the points: x=na (where n runs from 0 to N-1). Between the delta functions the wavefunction satisfies the free Schrödinger's equation:
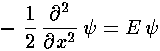
with solutions:
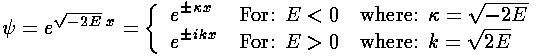
We assume in what follows that we are seeking bound state solutions
i.e., E<0, but if we seek unbound solutions, i.e.,
E>0, we need only change 
to ik.
Thus between the delta functions the wavefunction must be a linear combination of the rising and falling solutions, as shown above. The wavefunctions must be continuous across the delta function whereas the derivative of the wavefunction has a discontinuity:
-2
(0)+'(-)='(+)
We can use these results to connect our general Schrödinger's equation solution from one side of the delta function to the other side of the potential:
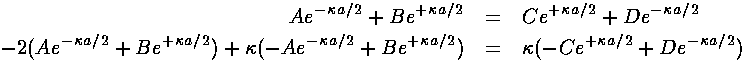
The structure of these equations is a bit clearer if we call the reoccuring expression:
exp(+a/2) = X
then:
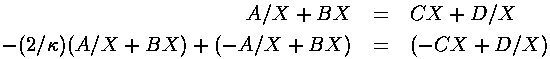
Adding and subtracting these equations yields:
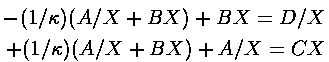
which we can cast in the form of a matrix equation:
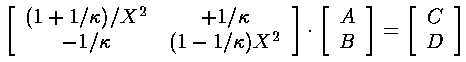
Let's give the matrix the name [M]
Now if we want to consider the next delta function in sequence, C and D become just like A and B, and we can find the linear combination in the following cell just by applying [M] to (C,D), i.e., by applying [M]2 to (A,B). Now before the first delta function, normalization requires that the A for that cell be zero. Thus (A,B) in all following cells can be calculated from
[M]j·(0,1)
In particular, after N delta functions the produced linear combination is given by:
[M]N·(0,1)
The "D" coefficient (bottom) must be zero if the
wavefunction beyond the delta function array is to be normalizable.
In general it will not be zero...that is to say most
will produce non-normalizable wavefunctions. We seek only those
that work, i.e., we seek zeros of the function:
(0,1)·[M()]N·(0,1)
The process of finding the roots of the above equation is made easier by some linear algebra. The matrix [M] has eigenvectors on which the action of [M] is trivial: just multiplication. Thus lets find the eigenvectors and values of [M]:
m={{(1+1/k)/x^2,1/k},{-1/k,x^2(1-1/k)}}
{{l1,l2},{v1,v2}}=Eigensystem[m]
Solve[{0,1}==a v1+b v2,{a,b}]
a l1^n v1 + b l2^n v2 /. First[%]
d[x_,a_,n_]= % /. k-> (2 Log[x])/a
k1=Log[Re[x]](2/4) /. FindRoot[Last[d[x,4,8]]==0,{x,6.83}]
psi[x_,k_,a_,n_]:=(If[x<0,Return[Exp[k(x+a/2)]]];itemp=Min[n-1,IntegerPart[x/a]]+1;
vtemp=d[Exp[k a/2],a,itemp];
Return[vtemp[[1]] Exp[-k(x-(itemp-1/2) a)]+vtemp[[2]] Exp[+k(x-(itemp-1/2) a)] ] )
Plot[psi[x,k1,4,8],{x,-4,32}]
We gotten way ahead of ourselves with that Mathematica
code. Once we have the eigenvectors vi
and eigenvalues 
i, we can expand our
initial (A,B)=(0,1) in terms of those vectors:
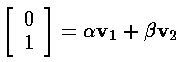
Now when [M]j acts on (0,1) the result is trivial:
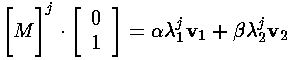
SO now we have an "easy" expression for the coefficients in
any cell, and in particular the last cell. We must now find
exactly those values of that give
no exponentially growing solution in the last cell.
No tricks here: just use the numerical root finder
in Mathematica. The root finder needs a starting value,
so it's helpful to plot out the coefficient of the last cells
exponentially growing part as a function of say X. Here is an example
for a=4, N=8.
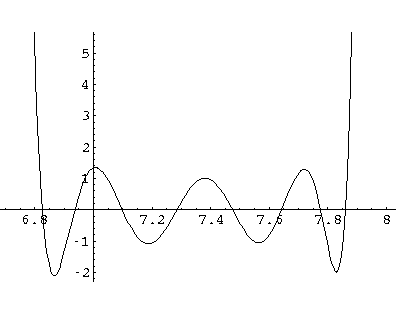
From each of these X roots, we can find a
and hence E.