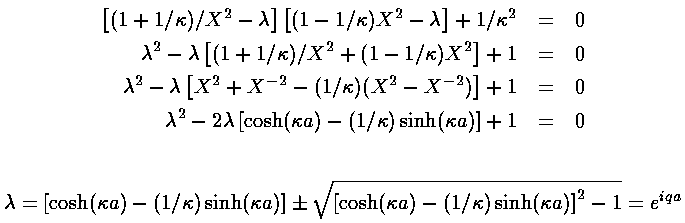
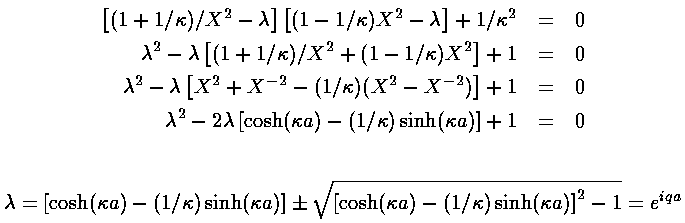
The roots of this equations (i.e., the eigenvalues) are either a complex-conjugate pair or a real number and its reciprocal (since the constant term in the quadratic is 1 the product of the eigenvalues is 1). The normalizable solutions discussed on the previous page must occur when the eigenvalues are complex-conjugate pair, i.e., when the discriminant is less than zero or:
1>cosh(
a)-(1/)sinh(a)>-1
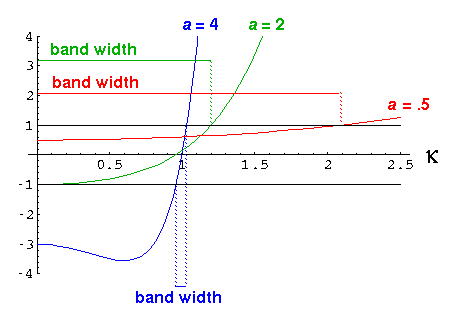
Below is a plot of the above function for various values of a.
Note that the y-intercept is 1-a, so the allowed
do not range down to zero if a>2.
Thus with weak overlap we have an entire band of E<0 states.
On the other hand if we have a<2 the band of states
extends up to (and beyond) E=0
It is useful to give this complex eigenvalue a name:
=exp(i qa)
Notice that as
cosh(a)-(1/)sinh(a)
ranges from -1 to 1 (as it does when a>2),
ranges from exp(i
) to
exp(i0). The low value of is the least bound (highest energy) state
and has q=/a. The high value of is the
most bound state (lowest energy) and has q=0.
Note that for the wavefunction generated from the eigenvector,
the wavefunction in the next cell is just
times the wavefunction in the current cell:
(x+a)= ei q a (x)
Thus there is a periodic function hidden in which we can extract:
uq(x) = (x)/ei qx
uq(x+a) = (x+a))/ei q(x+a)
=(x)/ei qx = uq(x)
We have basically come up with Floquet's theorem which states that if the coefficients of a
differential equation are periodic, there are solution's which are "almost" periodic in the above
sense: that can be written as an exponential times a periodic function:
(x) = ei qx uq(x)
q labels the solutions. These nearly periodic solutions are our solutions to the full (infinite) lattice.
As appropriate for an infinite lattice, we have an infinite number of eigenenergies labeled by q. If we wanted to consider a large but finite crystal with a large but finite number of levels, we could employ a quantum condition on q. In the usual case (periodic boundary conditions) the allowed values of q are given by:
qa = 2n/N, where n would basically range from -N/2 to +N/2
We can now plot out our eigenenergy as a function of q:
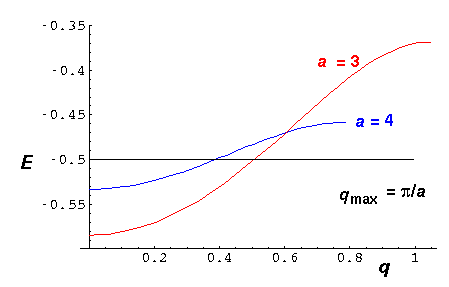
Note that for a=4 (in blue) the band is narrower and extends to smaller
qmax=/a. As we reduce a
to say a=3 (in red) the band widens. At a=2 it would extend up to
E=0.
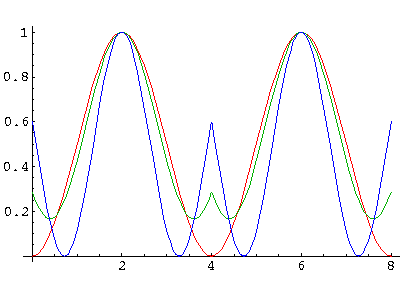
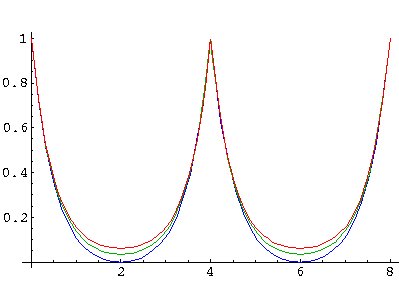
The wavefunctions for our infinite lattice are complex, but the probability density is periodic and varies a little over a band. Here are the results for a=4 as q varies over the entire band. Basically q=0 is the fully symmetric state, and qmax is the antisymmetric state.
While the probability density is periodic,
for the wavefunction
there is a slow oscillation between real and imaginary parts. Below is a plot of
the real part of a wavefunction with qa=/8, i.e.,
16 lattice spacings to make a period.
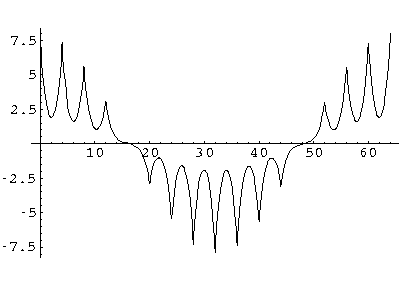
Note that q is a continuous variable, so there is no need for the wavefunction's long "period" to match the lattice.
We can of course, continue this game to positive energy solutions:
1>cos(ka)-(1/k)sin(ka)>-1
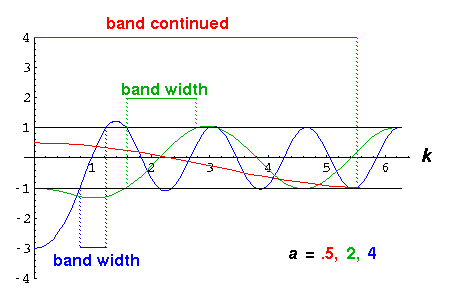
Notice that there are now an infinite number of bands, and that the band gaps shrink with increasing energy (k).
Here are the lowest three bands for a=4:
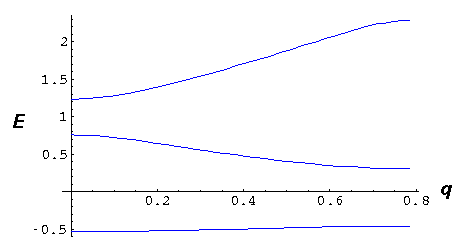
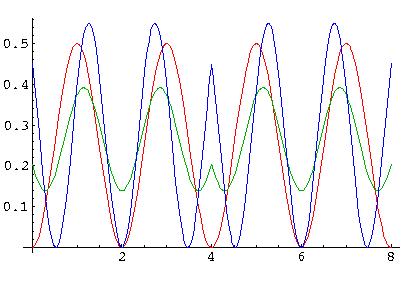
Within the wider bands there is more variation in the probability density. Here are results for the next two highest bands with probability densities plotted at band bottom, middle, and top.
