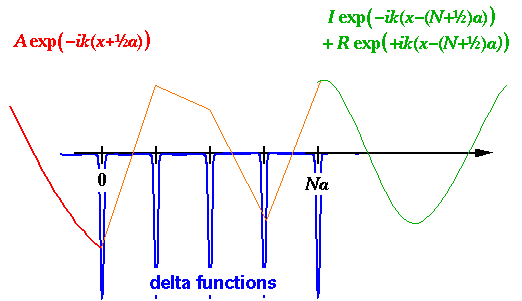

We have an incident beam on the far right moving towards the crystal: I exp(-i kx), the wave is partially transmitted into the crystal, where it is knocked around by the nuclei. Some of the wave emerges from the lhs as the transmitted wave: A exp(-i kx). There is also a reflected wave on the far right: R exp(+i kx). The above represents a switch from our past set-up (in which waves came in from the left) which we have instituted so we can use the machinery set up to find bound states. Thus we "start" with the transmitted wave (which consists of just one solution), connect it through N nuclei, and find what the incident and reflected waves must have been. Following our earlier work we have:
(I,R) = [M]N · (A,0)
We might as well make A=1, and our reflection probability (which,confusingly, we will also call R) will then be: |R|2/|I|2. We will, of course, use our eigenvectors to simplify calculation.
m={{(1-I/k)Exp[- I k a],-I/k},{I/k,(1+I/k)Exp[+ I k a]}}
{{l1,l2},{v1,v2}}=Eigensystem[m]
Solve[{1,0}==c v1+d v2,{c,d}]
c l1^n v1 + d l2^n v2 /. First[%]
ds[k_,a_,n_]= %
ref[k_,a_,n_]=Abs[Last[ds[k,a,n]]/First[ds[k,a,n]]]^2
ParametricPlot[{.5 k^2, ref[k,4,32]},{k,0,3}]
Here are some calculated reflection probabilities a a function of the incident beam energy for various crystal sizes:
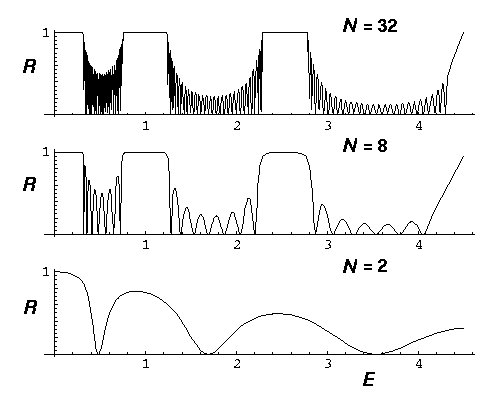
Note that at some energies the crystal is highly reflective. As the following picture shows, those highly reflective energies correspond to the band gaps.
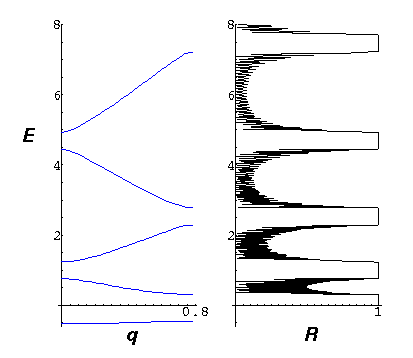
Mathematically this makes sense as the gaps are exactly where the eigenvalues are not of magnitude 1. There the waves must exponentially decay (or grow) in the crystal. In order to transmit a wave with A=1, the incident wave must be huge as the incident wave is exponentially damped in the crystal (and the energy is reflected back).
Alternatively you can say that what is happening is Bragg scattering of the incident wave. Inside the crystal the wavelength of the wave is determined by q not k. The gaps are then exactly the Bragg scattering condition.