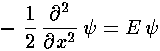
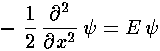
with solutions:
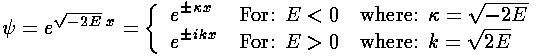
At first glance it looks like there are no bound-state (E<0)
solutions, because the exponential bound-state solutions grow without bound for
either x=+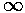
or -.
There seems to be no hope of normalizing these states!
(This is certainly the case for an actual free particle: only the oscillatory
E>0 solutions are allowed; As we have discussed,
they are also not
normalizable, but at least they remain finite.)
However, we haven't put the potential into the picture yet. So consider how the wavefunction must change near the singularity:
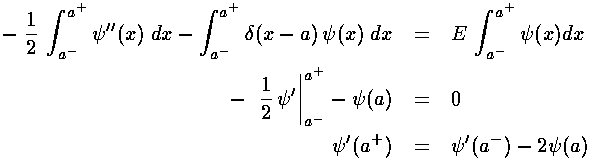
As we said on page 1, the result of the delta function is to cause a discontinuity in the slope. If we work things just right the rising exponential before the delta function can be turned into a falling exponential after the delta function...the result would be normalizable.
OK, let's put a single attractive delta function at the origin. In order to make normalizable functions we want:
= exp(+
x) for x<0
= exp(- x) for x>0
We adjust (i.e., E) until our discontinuity in
slope equation is satisfied:
- = - 2
= 1
Thus the energy of the one bound state is: E=-½.
For unbound solutions we seek solutions of the form:
= exp(i kx) + R exp(-i kx) for x<0
= T exp(i kx) for x>0
Wavefunction continuity requires:
1+R=T
Our discontinuity in slope equation says:
i kT = i k(1-R) - 2(1+R)
SO:
i k(1+R) = i k(1-R) - 2(1+R)
2i kR = - 2(1+R)
R = -1/(1+ik)
Thus for small k (low energy) we get 100% reflection, whereas for large k (high energy) we get 100% transmission.
If you are unsure of the meaning of these unbound solutions you may want to review earlier material.