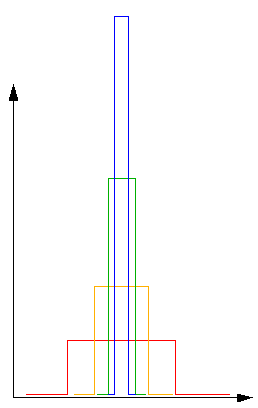
) "function" as the limit of a process
which starts with a square barrier, and reduces
the thickness of the barrier, but increases the height of the barrier
so that the area under the barrier function remains 1:
The result is a "function" that is zero almost everywhere, but is infinite at the one point (x=0) where the barriers have been centered. The "area" under this one point is 1. The eyes of your math TA may roll at the thought of such a "function", but direct her to, for example, Generalized Functions by Gel'fand & Shilov (QA331.G373) to learn how such a beast can be made mathematically legitimate. For physicists, the delta function is well designed to represent, for example, the charge density of a point particle: there is some total charge on the particle, but since the particle is point-like, the charge density is zero except at the single location of the particle.
Here are some basic properties of the delta function:
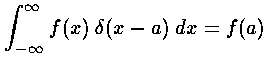
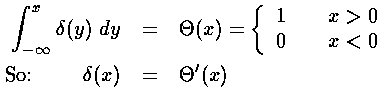
That last property is worth stressing. Consider the following tower of functions. You move down the tower by integrating (as in the above example); you move up the tower by differentiating. Recall when we worked with square well potentials we had wave functions that had jumps in curvature (discontinuous second derivative), so that in Schrödinger's equation taking the second derivate of the wavefunction produced a step to make the step in the potential.
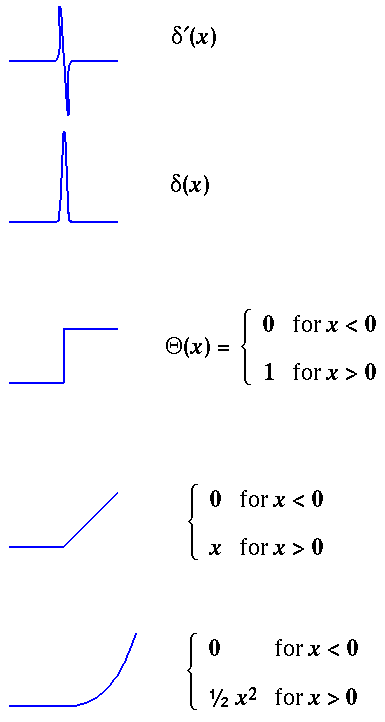
On these pages we will be considering a delta function potential, so our wave function will have to have a jump in derivative so that when Schrödinger's equation takes the second derivate of the wavefunction the result is a delta function to match the delta function potential.
Classically it's hard to make much sense of delta function potentials.
A delta function potential causes no force, except at the one point the potential
is non-zero.
A barrier potential (+(x)) would have an
infinitely thin disallowed region: I guess classically this would reflect
all incident particles. An attractive potential
(-(x)) would instantaneously accelerate and then
deaccelerate any particle that reached its non-zero point...but all effects would
be limited to that instant. Classically a particle could sit unmoving right
on top of the infinite (but zero thickness) well...I guess we'd have to say
that in that condition the particle had negative infinity potential and total
energy.
In quantum mechanics the idea is that the "attractive" (i.e., negative) delta function potential provides a computationally simple model for any "short"-range force: for example the strongly attractive but "short" range nuclear force. The key question is what do we mean by "short" in the above: short compared to what? Generally the answer is short compared to the range (or wavelength) of the wavefunction.