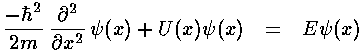
Our aim is to solve the time independent Schrödinger's equation to find the probability amplitude (i.e., the wavefunction) as a function of position.
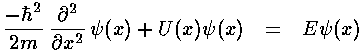
where U(x) consists of linear combinations
of Dirac delta functions with singular points at various locations.
(
(x-a) has its singular point
at x=a.)
As usual our first step is to look at units and seek a dimensionless
version of Schrödinger's equation. We immediately find an anomaly:
is a function which has units (if its argument
has units). Look at the fundamental properties of :
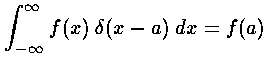
f, of course, has the same units on both sides of the
equation, so the units of must cancel the
units of dx...i.e., the units of
are the reciprocal of the units of its argument.
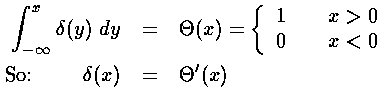
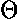is unitless (0 or 1) and so the units
of 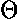' = d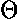/dx
come just from the dx in the denominator. Again
the units of
are the reciprocal of the units of its argument.
Thus if we make a potential energy:
U(x)=w(x-a),
has the units of 1/length (since x
has units of length) so w must have units of energy·length.
2/m=A has the
units of energy·length2.
Thus we can make our length scale L=A/w, and our energy scale e=w2/A.
The algebra of this conversion can be a little tricky we note:
(x)= (x'·L)=
(1/L) (x')
So our dimensionless version of Schrödinger's equation becomes:
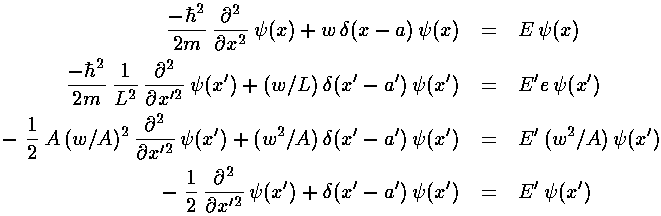
In the following pages we will drop all primes, so beware that on the following pages x' is called simply x.
Note that our strength of potential w has completely disappeared. It is, of course, still present in our length and energy scale factors. Thus shrinking the dimensionless location of all delta function singularities corresponds to fixed real-space positions with a reduced potential.
Note that we will mostly be considering attractive delta function
potentials so our Schrödinger's equation will have -
rather than the + shown above.