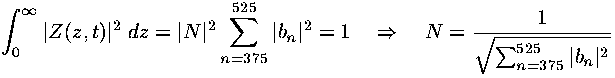Falling p.15

Projects for you!

The below is a list of project you should be able to complete. For some of the projects Mathematica may be of use. Here's a file containing the Mathematica I used to make these pages.

How could "probability density" be measured? Consider an imaginary device which, on command, produces an electron in a particular wavefunction . We have the device produce an electron in this particular state and then measure the electron's position. Of course, we get different answers every time we use the device: position would be a "random variable". This file contains the results of 1000 position measurements. (I've sorted the position measurements: from highest to lowest-- repeated measurements of position would produce patternless results.) Your job is to plot the probability density as a function of position. A complete answer would include estimates of the probability density (with error!) at various positions.
We have used the energy and length scales: e and l and the related time and momentum scales (/e and /l).
1. Show that classical equation of motion:
  z(t)=z₀-½gt²
  becomes:
  z'(t')=z'₀-t'²
  in our dimensionless variables.
2. Using the data on p.6 show that this is in fact how the expectation value of position is moving.
3. Show that the dimensionless variables behave as if m=½ in that for example, if the dimensionless momentum p'=1, the dimensionless velocity (length/time) v'=2 and the dimensionless kinetic energy is 2.
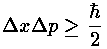
Heisenberg's uncertainty principal states that the product of uncertainties in x and p must be hbar/2 or more:

Find 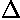z' and 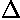p' for the eigenfunctions: n=1,2,4,8,16. (Hint: the p' operator is just -i × the derivative w.r.t. z'; of course it's hermitian). Plot the uncertainty product vs n. What seems to be the relationship between the two. Explain.
Look up the virial theorem in a quantum mechanics textbook; prove the result and show how the general result proves what we needed in the perturbation theory section.
The actually infinite potential for z<0 is not physically possible. If we replace that potential with more possible potentials, how will the eigen-energies and functions change? If the Schrödinger's equation with the replacement potential can be solved, then what is required is to match those solutions for z<0 with the Airy functions for z>0.
The easiest solution for Schrödinger's equation (see example ½) is the constant potential: V(z')=V₀. If E<V₀, we still have a turning point at z=0, i.e., the ball will still bounce up from the floor. Of course, it will "tunnel" a bit into the classically disallowed region of z<0; in fact the solution to Schrödinger's equation is just an exponential: =exp(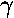z') where 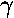=(V₀-E')^½. 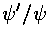Matching the wavefunctions at z'=0 amounts to equating the "logarithmic derivative" of the wavefunction: at z'=0^- to the same at z'=0⁺, i.e.,

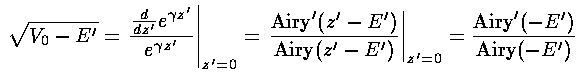
The below displays the resulting energy shifts if V₀=10 (black energy levels are for infinite potential, red for finite [10] potential).

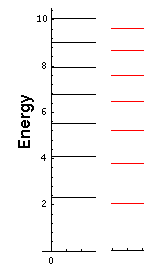
Pick some value for V₀ and calculate the the energy levels for that modified potential.
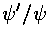Another possible choice for the z<0 potential is another linear potential, this time one producing a constant (and much larger) upward force. The solution for the z>0 remains: Ai(z/l_R-E/e_R) with e_R and l_R as appropriate for z>0, and Ai(-z/l_L-E/e_L) with e_L and l_L as appropriate for z<0. Matching the "logarithmic derivative" of the wavefunction: at z'=0^- to the same at z'=0⁺, i.e.,

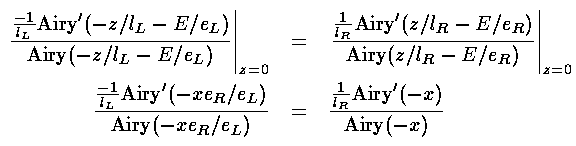
where x is E/e_R. In the particular case that the force on the left is 27 times the force on the right: l_L=l_R/3 and e_L=9e_R. The resulting energy levels are displayed in red below (black is the usual infinite potential case).

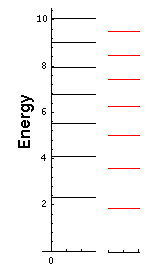
Pick some value for the left-side force and calculate the the energy levels for that modified potential.
The above equation for the energy is simplified if the left-side force equals (in magnitude) the right-side force. The only solutions are Ai(-x)=0 and Ai'(-x)=0. The former are solutions with odd symmetry. For that reason these solutions have =0 at z=0, and hence are identical (on the rhs) to our usual infinite-potential solutions. The latter are solutions have even symmetry. The even and odd solutions alternate with the even ground state at E'=1.019.
Make a stacked wavefunction plot of the first 5 energy eigenfunctions for this symmetric two-force problem (i.e., with V=|z'|). Be sure to include the plot of potential energy on this same plot.
The bouncing ball is known to be in the n=16 state when the infinite potential is removed and replaced with a lhs force identical in magnitude (but pushing up) to that on the rhs. Find the 7 states in which the bouncing-ball is now mostly likely to be found. Calculate the weighted average and standard deviation of those energies. Must we observe that the particle's energy is conserved? Using those 7 states (with proper time dependence), plot the position-probabilities for several times near when the infinite potential is removed, and for a time one classical period (in the two-force situation) and ½ classical period after the infinite potential is removed. (It's easiest to plot the z'<0 and z'>0 separately.)
Reproduce the falling ball solution described on p.7 with some other initial wavefunction. Produce plots and tables showing the results.
WKB
1. Why is it N+¾ rather than N+½?
2. The falling QM ball is based on a energy eigenfunction with E' near 122.2. Find more significant digits for the energy and determine what n has this energy.
3. In the case of the 27× lhs force, the energy of the 10th state is about: 12.2842. What would WKB predict (i.e., do WKB for two-sided linear case)?
4. Find the WKB approximation for the energy in the symmetric two-force situation.
Rayleigh-Ritz
1. Confirm the reported results for f(z')=z' exp(-az').
2. Find the RR estimate for the groundstate energy using f(z')=z' exp(-az'²).
3. Find the RR estimate for the groundstate energy using f(z')=z' exp(-az'^3/2).
4. Pick your own f(z').
5. Plot the above four wavefunctions along with the exact Airy function solution.
Rayleigh-Ritz. There is no reason to limit the number of adjustable parameters in our trial wavefunction (other than that it then becomes a more difficult problem to find the minimum). Pick a trial wavefunction with with two adjustable parameters (e.g., f(z')=z'(1+bz'²) exp(-az'²) ) and find the expectation value for H as a function of the two parameters (e.g., a and b). Make a contour plot of the result to identify an approximate best value and then use Mathematica's FindMinimum or similar program to get the best possible RR bound. Plot the resulting wavefunction along with the exact wavefunction.
Perturbation Theory: Consider a perturbing potential which for 0<z'<a is V'=a-z', and otherwise V'=0. This results in a total potential that is constant (total P.E.=a) if 0<z'<a and exactly equals our old potential otherwise.

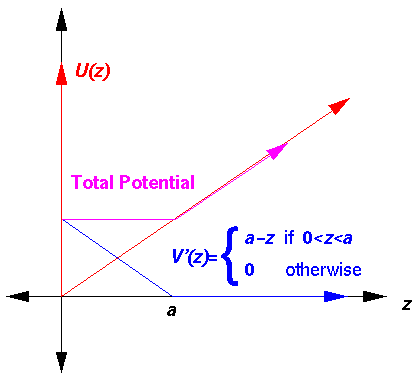
The above total potential can be "easily" solved. For 0<z'<a Schrödinger's equation solution is sin(kz') where k²=E'-a. For z'>a, we have our usual Airy solutions: Ai(z'-E'). As usual we find eigenenergies by solving the equation that comes from matching the logarithmic derivatives at z'=a.

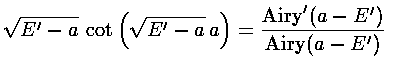
The below plot shows how the energy levels for n=1,2 change as a function of a. Note that perturbation theory tracks the exact result until about a=1.5 for n=1 and a=3.5 for n=2. Note that in both cases the perturbation theory result is a bit above the exact result.
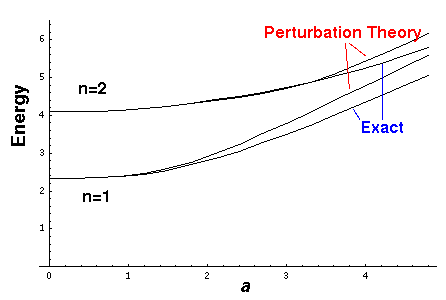
1. Pick some value of n and plot how perturbation theory tracks the exact result.
2. For any problem we are guaranteed that the perturbation theory result for the ground state lies above the exact result. Why?
3. Second order perturbation requires an infinite sum of numerical integrals, and is therefore hard to calculate completely. Calculate the second order correction for a=2 and n=1 including terms through n=10. Compare to the exact result.
Consider the displacement operator, D_c, defined by:
D_c f(x) = f(x+c)
1. Show that D_c is a linear operator.
2. Find the inverse of D_c. Find the Hermitian conjugate of D_c. Is D_c Hermitian? Unitary? etc.
3. Show that
  D_c f(x) = exp(i pc/) f(x)
  where p is the momentum operator, is Taylor's expansion. Using this equation, find the Hermitian conjugate of D_c.
4. Carefully show that D_c commutes with the derivative operator d/dx (and hence [D_c, p] = 0).
5. Consider the 1-d Hamiltonian H for the linear potential U=z for all z, even z<0. Show:
  [H,D_c] = -c D_c
  Use this relationship to show that if is an energy eigenfunction with energy E, then D_c is an energy eigenfunction with energy E-c. (This problem is important in the usual treatment of raising and lowering operators in SHM. See any QM textbook -- my treatment on SHM p.8 is intensionally unusual.)
6. Show that state D_c is normalized if is normalized. (In the usual treatment of lowering operators one finds that repeatedly lowering a state must eventually produce a zero-normed state.)
On these pages we made a "2d" falling problem by adding a force-free dimension (y) to a constant-force dimension (z). Another option would be to make the y dimension also have a constant-force (but perhaps with a different strength force than in the z direction). In this case the constant force F would be constant but with different components in the y and z directions. We might as well orient the force in the vertical direction by rotating our axes. Thus:
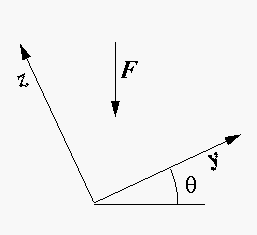
1. Solve Schrödinger's equation in this case, reporting the eigenenergies and wavefunctions in terms of the normal (dimensioned!) variables (like y, z, F_y, F_z, m, ).
2. Write down the ground state energy as a function of for fixed |F|.
3. Since we observe energy differences as emitted photon energies, energy differences are in some sense more fundamental than energies. Plot both the ground state energy and the first excited energy as a function of so you can see how the energy difference depends on .
4. Consider the cases =45° and 30°. Calculate the energies of the lowest 8 eigenstates. Plot the results.
  
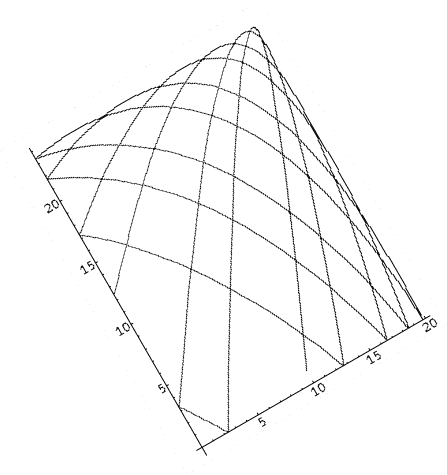
  For comparison, the above is an example of the Newtonian trajectory for this potential...follow the bouncing ball!
In the above problem you have found the eigenenergy of various states as a function of . Consider the effect of a small change in in first order perturbation theory, i.e.,
U = cos z + sin y
U' = (-sin z + cos y)
Compare the results of perturbation theory to the exact result.
Show that is the standard deviation of the wavefunction:
= N exp(-y'²/4²) exp(i k₀y')
What is the mean position? Find the mean momentum of this wavefunction and the standard deviation of the momentum. What is the value of the Heisenberg Uncertainty product in this case?
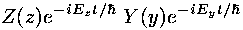
On page 11 I claimed that the following is a solution to the time dependent Schrödinger's equation:

Prove this. Show also that the final "quantum cannon" wavefunction is a linear combination of terms like the above and hence also a solution to the time dependent Schrödinger's equation.
On page 11. I commented:
I claim that this kind of messy solves our time-dependent Schrödinger's equation. This task is left for a problem.

where the reference is to the force-free motion in in the y direction of the 2d fall, which was derived as follows:

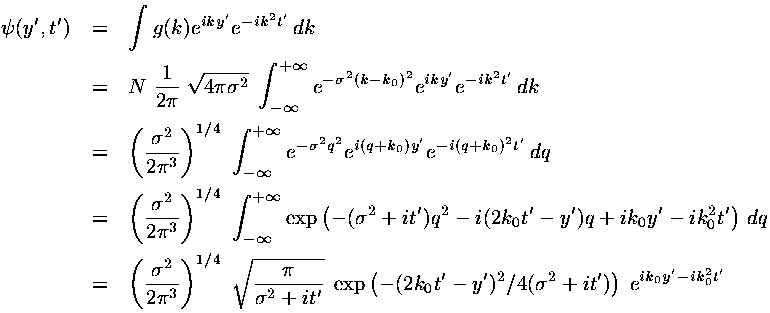
Starting with the last formula, show directly (perhaps using Mathematica) that this is a solution to the time-dependent Schrödinger's equation.
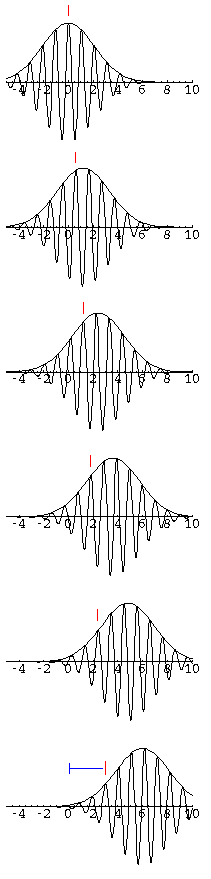
Using your own words define group velocity and phase velocity. Consider the following sequence of pictures taken at t=0, 0.1, 0.2, 0.3, .. (this appeared on page 12).

Use these plots to calculate the phase and group velocity displayed in this packet.
Using the graphs on page 13 estimate the average z position of the wave-packet at the various times. Enter the data into a fitting program and fit the data to the expected quadratic:
z(t)=z₀+v₀t+½at²
Compare the fit parameters to those expected from the construction of the wave-packet.
Following the methods on page 13 find b_n that approximate some other initial wavefunction.
Combine your above wavefunction with a y wavefunction to fire the quantum cannon using your initial conditions.
Provide the missing steps for these results from page 13.

Return