SHM p.8

Raising and Lowering Operators

Any set of orthogonal polynomials must satisfy an equation like (why?):

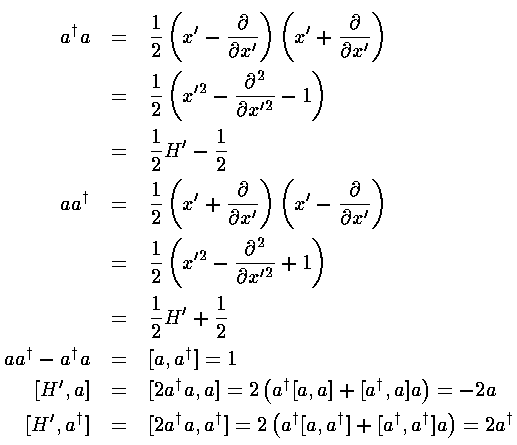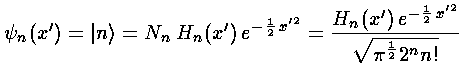
xPn(x) = anPn+1(x) + bnPn(x) + cnPn-1(x)

In the case of polynomials with definite even/odd parity, bn=0 (why?). For Hermite polynomials we have:

x Hn(x) = ½ Hn+1(x) + n Hn-1(x)

All the classical orthogonal polynomials satisfy equations like:

an(x) P'n(x) = bn(x) Pn(x) + cn(x) Pn-1(x)

For Hermite polynomials we have:

H'n(x) = 2n Hn-1(x)

Since

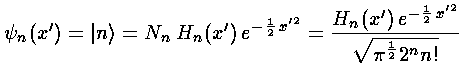
we can relate the results of simple operations on an eigenfunction in terms of other eigenfunctions

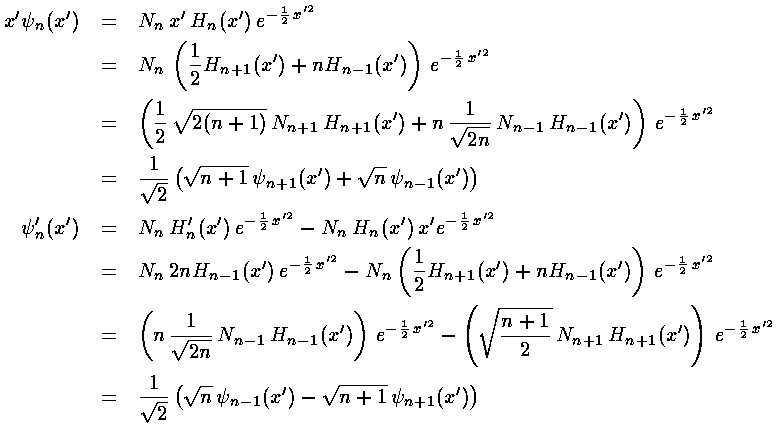
By themselves these results are useful, e.g., to calculate integrals like: <n|x'2|n> or <n|p2|n>, but they find their most common use by combining the results into raising and lowering operators:

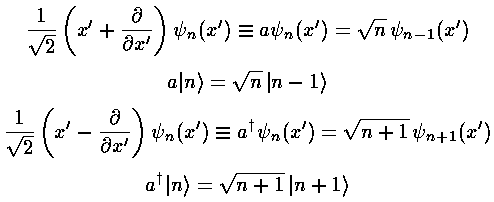
We note the following properties of the raising and lowering operators:

Next