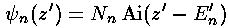
Our normalized energy eigenfunctions are displaced Airy functions:
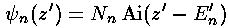
These eigenfunctions are orthogonal:
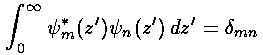
So if we try to express a given function f(z') in terms of a sum of these functions:
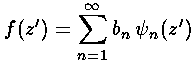
orthogonality allows us to solve for the bn:
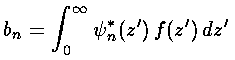
To see how this probability lump moves with time, we need only use the time dependence of the energy eigenfunctions:
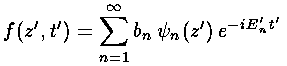
 = N exp(-y'2/4
= N exp(-y'2/4 2)
exp(i k0y')
2)
exp(i k0y')
We need to modify it only a bit to use it for the initial state of our
z motion. First, since U= for
z<0,
for
z<0,  =0 for
z<0. The gaussian wave=packet is never actually zero, just very
small several
=0 for
z<0. The gaussian wave=packet is never actually zero, just very
small several  s away from the peak.
Thus if we continue to use a gaussian form, we must
raise its CM location by several
s away from the peak.
Thus if we continue to use a gaussian form, we must
raise its CM location by several  . Thus we limit the discontinuity
at z=0 by making
. Thus we limit the discontinuity
at z=0 by making
 small for positive z near 0 (whereas
small for positive z near 0 (whereas
 =0 for z<0). Thus we are led to an
initial wavefunction:
=0 for z<0). Thus we are led to an
initial wavefunction:
f(z) = exp(-(z-z0)2/4 2)
exp(i kz0z)
2)
exp(i kz0z)
where z0/ >> 1, so f(0+) is
small. As before we must chose
>> 1, so f(0+) is
small. As before we must chose  relatively large if we want
a narrow range of velocities in the wave-packet. We then proceed to calculate the
bn exactly as above. I chose kz0=12,
relatively large if we want
a narrow range of velocities in the wave-packet. We then proceed to calculate the
bn exactly as above. I chose kz0=12,
 =5, z0=20. I cannot actually find
and infinite number of bn, so I restrict my sum about 150
n values whose eigenenergies are near the expected value of:
=5, z0=20. I cannot actually find
and infinite number of bn, so I restrict my sum about 150
n values whose eigenenergies are near the expected value of:
kz02 + z0 = 164
which occurs near n=450. Since I have not included the complete set of orthonormal wavefunctions in the sum, my solution to Schrödinger's equation will not exactly equal the gaussian form. (Furthermore I did not normalize my above f(z).) Hence I will want to normalize my finite-sum solution:
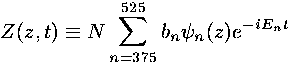
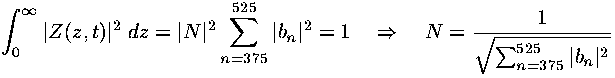
Thus we have found our solution to the time dependent Schrödinger's equation for motion in the z direction which is a particular a superposition of single-energy solutions making a lump of probability that moves.
Here are some pictures of the probability density as it moves first up and then down:
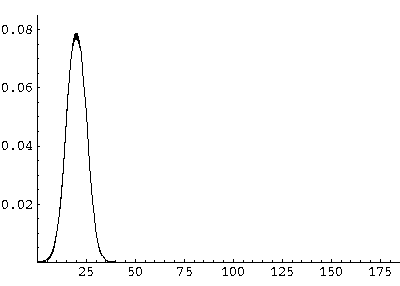
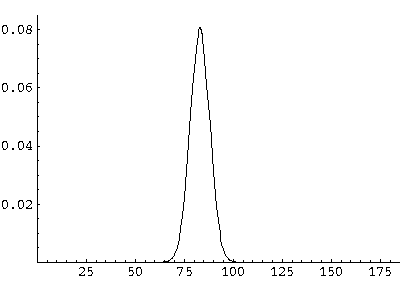
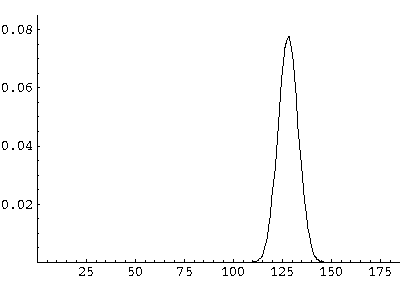
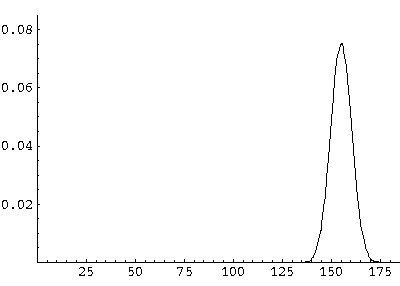
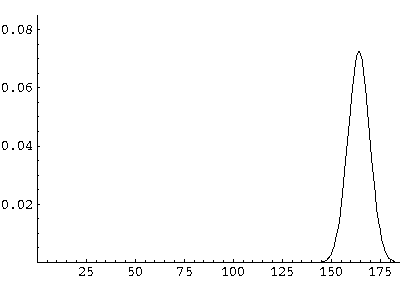
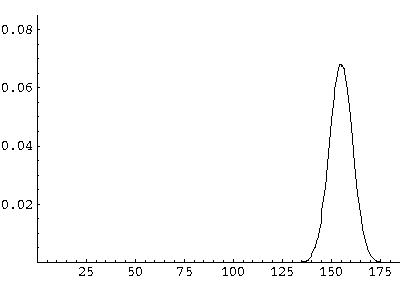
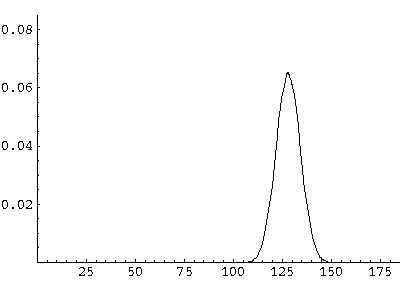
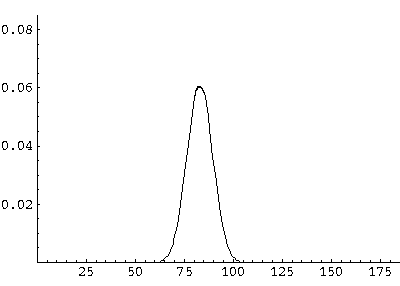
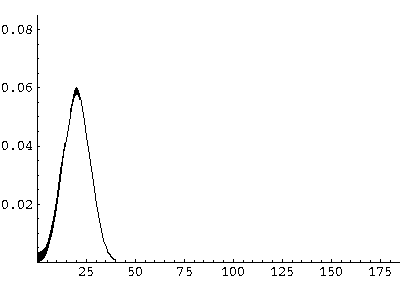
All of these features can be seen in greater detail by examining the following QuickTime movie (0.2 Mb) on a frame-by-frame basis.