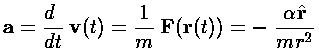
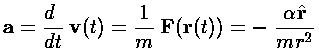
In quantum mechanics the primary aim is to solve the time independent Schrödinger's equation to find the probability amplitude (i.e., the wavefunction) as a function of position.
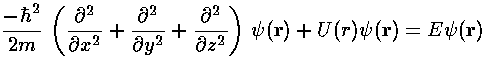
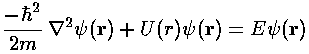
Note again the huge shift between classical mechanics and quantum mechanics: what was the dependent variable in classical mechanics (r) has become the independent variable; what was the independent variable (t) has disappeared. We've previously seen (in falling, SHM 1d and SHM 2d) how motion is possible if time plays no role. It turns out energy (E) is more measurable than motion, hence energy has replaced time as the most important variable.
Almost any "real" problem in classical mechanics (e.g., a real cannon ball flying through the Earth's atmosphere) is so complex that it cannot be solved using paper-and-pencil methods: the differential equation must be solved "numerically" using a computer. Quantum mechanics only makes things more difficult. Only the simplest examples have "analytical" solutions (i.e., the answer can be written down using "well known" functions). The purpose of these textbook problems is to provide examples where all the dependencies are explicit so that they are available for play/understanding.
If a problem has an analytical solution, say,
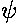=f(x)
where f(x) is some "well-known" function, consider the
consequences. Just about "every-known" function requires
that its argument be dimensionless. (I can think of only two
counterexamples.) Thus 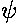=sin(x),
or 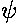=exp(-x2) cannot be
proper answers if x has the units...you cannot take
the sine of 1 meter, nor have a power that is 1 square-meter.
Thus answers must be of the form:
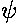=f(x/L)
where L "sets the scale" of the problem, i.e., has units that cancel those of x. Thus the first point-of-attack on any physics problem is to determine how you could form quantities like L that allow you to form dimensionless quantities like x/L.
In the classical mechanics problem, we have "givens" that
include the initial position r0 and velocity
v0 to use in forming dimensionless quantities.
Not so in the quantum mechanical problem as there is
no single position or velocity. Thus the quantities
we may build our dimensionless quantities from are just those
parameters in the Schrödinger's equation:
, 
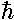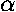, and m. In particular, Schrödinger's
equation has constants: 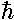2/2m=A
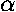and =B. B has the units of
energy·length=force·length2.
A has the units of
energy·length2=force·length3.
Thus L=A/B has units of length
and B/L=B2/A
has the units of energy. Instead of exactly these length and
energy scales, it is common to use as a length scale
the bohr radius length: l=2A/B (often denoted a0)
and the hartree as the energy scale:
e=B/l=½B2/A.
It is worthwhile to calculate the numerical value of these scales
and see how easy it would be to observe the quantum mechanical orbit.
| particle | force | length scale (bohr radius) | energy scale (hartree) |
|---|---|---|---|
| H atom | -e2/r2 | 0.53 Å | 27.2 eV |
| Ne atom (Z=10) | -Ze2/r2 | 5.29 pm | 2.72 keV |
| U atom (Z=92) | -Ze2/r2 | 575. fm | 0.23 MeV |
| positronium (e+e-) | -e2/r2 | 1.06 Å | 13.6 eV |
| muonium (µ+µ-) | -e2/r2 | 256. fm | 2.81 keV |
| protonium (p+p-) | -e2/r2 | 57.7 fm | 25.0 keV |
(Note: 1 Å = 10-10 m, p=pico=10-12, f=femto=10-15.)
(Note: Only the "oniums" [particle/anti-particle pair] values have been adjusted for reduced mass.)
Note that for all but protonium, the bohr radius is much larger than the strong force range (i.e., nuclear "size" of a few fm) so the force is approximately just electrostatic. In the case of the U atom the energy is becoming a fair fraction of the rest mass of the electron; the electron speed commonly exceeds 0.1c, so instead of Schrödinger's equation a relativistically correct equation should be used (e.g., Dirac equation).