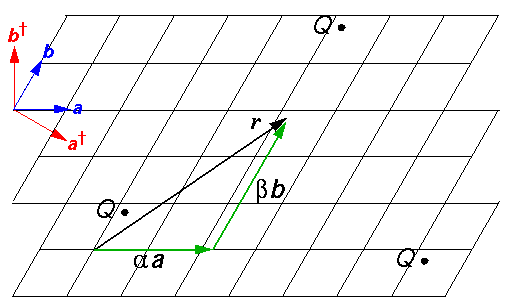
Consider the above picture of our hexangular lattice tiled with rhombuses. If a function, f, is periodic on the lattice, it means that that f(r) and f at all of the points Q share the same value. f(r) only cares about r's location relative to the rhombus that encloses it.
The function f thus needs to throw away all the parts of r that have to do with translation, and just focus on the remaining bit of r. Thus we seek to write r in terms of our basis vectors a and b. It should be clear that r can always be written as a linear combination of a and b (i.e., that a and b span the space), but how do we find the particular linear combination that works:
r =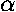 
a + 
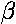b
The job of finding this linear combination is made easier by
constructing the vectors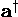 
and
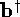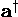. is constructed so
that it is perpendicular to b and is scaled so that
when dotted with a it yields 1. (Since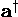
makes and angle of 30° with a, the length of
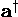is 1/[a cos(30°)]. The fact that, in dimensioned variables,
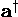has the units of reciprocal length, contributes to
the name reciprocal space.) Now if we dot both side of the above
equation with 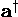, the 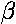term
drops out (since 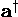is perpendicular to b)
and since a·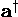=1 we have:
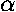= r·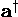
Similarly:
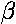= r·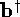
Now f needs to ignore the whole number parts of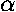
and 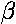, as the fraction parts state where r is in the base
rhombus. One way of ignoring the whole number parts is via periodic functions
like the trigonometric functions sine and cosine. For example,
cos(2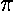
)
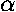will throw away the whole number part of 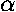, since
the integer part just adds
an integer number of 2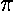 to the argument of cosine. More generally,
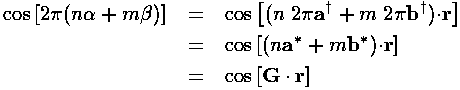
is periodic.
Notice that we have defined 2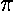-stretched versions of
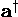and 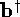denoted a* and b*.
These vectors are the basis vectors for our reciprocal lattice...i.e., we can
form a lattice by adding integer multiples of a* and b*,
just as we formed a real-space lattice by adding
integer multiples of a and b. G is an example of such
a vector built from an integer linear combination of
a* and b*.
From the magic of Fourier series, you know that you can build up
an arbitrary periodic function by putting together a sum of harmonics of
fundamental sine and cosine. This corresponds making linear combinations of terms like
exp(i G·r)
Where the various Gs are on the reciprocal lattice generated by a* and b*
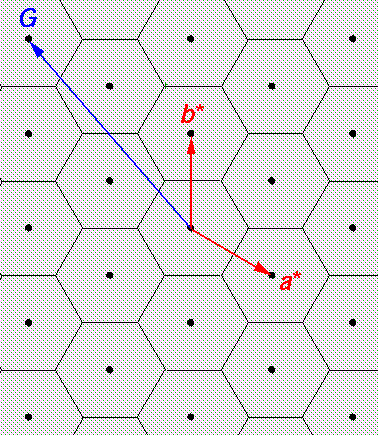
The above is a piece of reciprocal space. Each black dot is a reciprocal lattice vector. In particular reciprocal lattice vector G is:
G = b* -2 a*
Currently there is no particular meaning attached to the honey-comb that fills the lattice. You may note that, like the real lattice, the reciprocal lattice is hexangular closest packed. It is, however, rotated 90° compared to the real lattice.
In our dimensionless units the length of a* or
b* is 4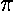/3½,
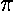a hexagon side is: 4/3, which is also the "radius"
of the hexagon.
Let me remind you of the key feature in all of this:
exp(i G·r)
is periodic on the real lattice if G is on the reciprocal lattice. If G=a*, exp(i G·r) is a wave with wavefront parallel to b, and hence traveling in a direction perpendicular to b; its wavelength is sized so that it exactly fits in the unit cell. If G=2a*, two wavelengths fit in the unit cell, etc. Similarly if G=b* the wavefront is parallel to a and one wavelength fits in the unit cell.
Ok, now lets go back to the Block form of the wavefunction:
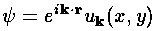
Notice that k is a little poorly defined, since if we reduce k by a reciprocal lattice vector G, we form a new u function (but not a different physical state) directly related to the original:
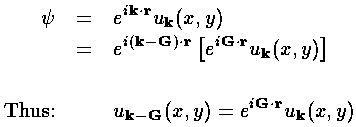
Thus we are in danger of multiple counting of states. If we let k range over so large a domain that, for some k both k and k-G are included in the domain, we have double counted the one state. This is the purpose of the honey-comb fill of our reciprocal lattice: if we restrict k to one of these cells (say the one that includes k=0) we avoid having both k and k-G in the domain. The hexagonal cell is created by going half way to the nearby reciprocal lattice vectors. This cell is known as the Brillouin zone.
If we know the band structure (E(k)) for k in a Brillouin zone, we know it for all k [but all this extended knowledge is redundant].