NPN Characteristic Curves

Measured Characteristic Curves for 2N3904

for I_B = 10 µA, 20 µA, 30 µA, ... , 80 µA

big data file, smaller data file, postscript plot, pdf plot

The behavior of an NPN bipolar transistor is largely controlled by the current flowing into the base (i.e., a positive current). For the usual collector-emitter voltage drops (i.e., the active region: positive voltages from a fraction of a volt up to some breakdown voltage) the collector current (I_C) is nearly independent of the collector-emitter voltage (V_CE), and instead depends on the base current (I_B). (This is unusual behavior: usually more voltage produces to more current, but here the current only increases slightly with increasing V_CE.) The current gain, i.e., the ratio of the collector current to the base current, is often denoted by 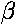or h_FE:

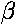= h_FE = I_C/I_B

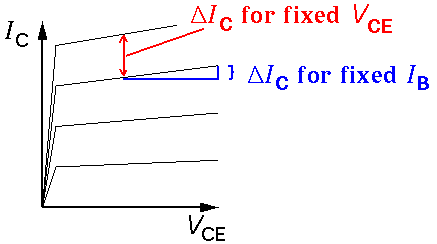
Thus in the simplest approximation the characteristic curves of a NPN are a set of flat, evenly spaced, lines:

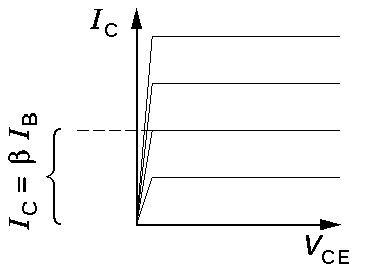
Each (flat) curve shows that I_C doesn't change with changing V_CE. The different levels show that I_C does depend on I_B.

A slightly more complicated approximation takes into account the sloping characteristic curves through the fiction of a constant Early Voltage (V_A). Here we assume that the characteristic curves all have a common x-axis intercept at the large negative voltage -V_A. (The dashed curves are far from the active region and in no way represent the actual behavior of the transistor for negative V_CE. In fact, the transistor is not designed to be operated with negative V_CE.)

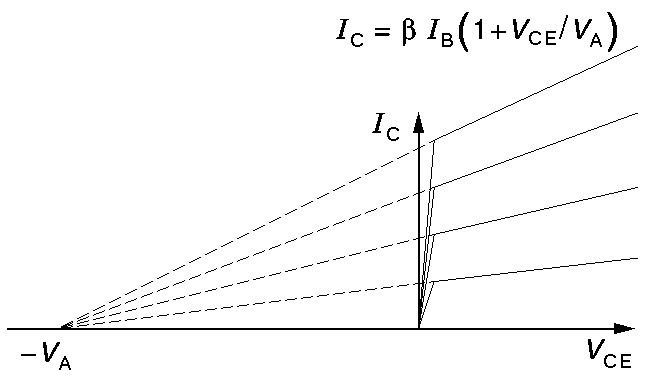
(For the above measured 2N3904, the Early voltage ranges from 100 to 150 V. That is the extrapolated characteristic curves do not intersect at a point.)

The actual relationship between the collector current (I_C) and the controlling base current (I_B) and collector-emitter voltage drop (V_CE) is some complicated function which we can denote:

I_C(I_B,V_CE)

Like any function we can approximate it near a particular point using just the first terms of a Taylors expansion:

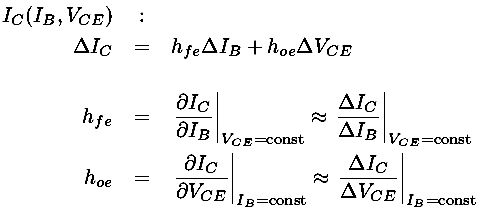
Clearly these hybrid (h) parameters are not constants. For example h_oe is the slope of a characteristic curve, which is nearly zero for small I_B and increases for larger I_B. (Note that slope on an I-V is basically the inverse of the resistance. Thus 1/h_oe can be described as the output impedance. A typical value for 1/h_oe would be 100,000 .)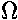

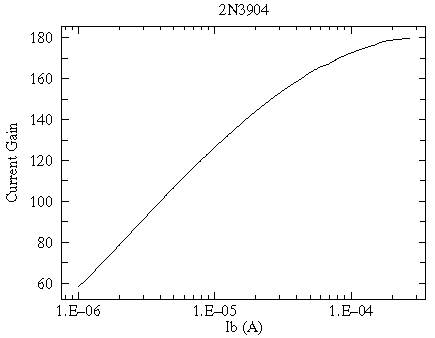
Even the defining parameter -- the current gain 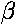or h_FE -- is not particularly constant and depends on I_B. Here is the measured relationship for the above 2N3904:

The characteristic curves focus on the output of the transistor, but we can also consider the behavior of the input. In the active region the base is a forward biased diode, and so V_B would be about .7 V, typical for a conducting Si diode. Of course in greater detail the relationship between V_B and I_B would be given by the Shockley diode equation:

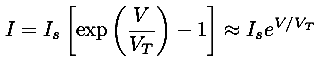
where I_s is a constant and the thermal voltage V_T is given by:

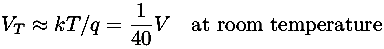
Because of the exponential relationship between base current and base voltage, the slope of this relationship (which could be called the input conductance, or 1/r_B, or 1/h_ie) can be approximated by:

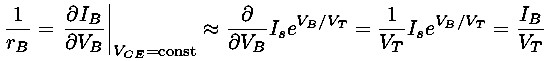
where in the last equation (25 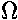/I_B) the base current must be entered in mA.

A desirable characteristic of a transistor is that the outputs have little effect on the inputs, but if we look in detail we find that V_CE affects V_B. The actual functional relationship giving the base voltage (V_B) from the base current (I_B) and collector-emitter voltage drop (V_CE) is some complicated function which we can denote:

V_B(I_B,V_CE)

Like any function we can again approximate it near a particular point using just the first terms of Taylors expansion:

The small value of h_re shows that the input is largely unaffected by the output.

The spec sheet reports the following values for the 2N3904:

Characteristics	Symbol	Min	Max	Unit
Input Impedance	hie	1	10	k Ohms
Voltage Feedback Ratio	hre	0.5	8	×10-4
Small-Signal Current Gain	hfe	100	400
Output Admittance	hoe	1.0	40	µ mhos