A B C D a b c d e f g 0 0 0 0 1 1 1 1 1 1 0 0 0 0 1 0 1 1 0 0 0 0 0 0 1 0 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 0 0 1 0 1 0 0 0 1 1 0 0 1 1 0 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1 0 1 1 1 1 1 1 0 0 0 0 1 0 0 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 1 1
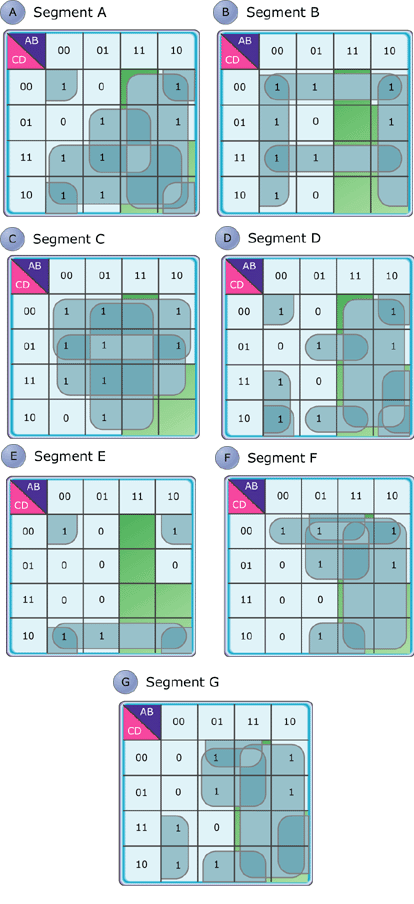
Figure 6A-G: Karnaugh maps for seven segments
My Karnaugh maps are shown in Figures 6A through 6G. Notice the heavy
use of don't-care states to minimize the equations. Any time we can let
the selected regions overlap the don't-care regions, we simplify the
equations. None of the equations are trivially simple; when the Arabs
invented the symbols for our decimal digits, they didn't plan ahead to
computer implementations, so we have to use the symbols we're given.
Even so, some patterns emerge, and we do spot certain terms, such a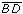s 
,
which recur in multiple segments. My best attempt at implementing the
equations goes like this:
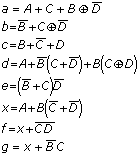
How does that compare with your own solutions?
Jack Crenshaw is a senior software engineer at Spectrum-Astro and the author of Math Toolkit for Real-Time Programming, from CMP Books. He holds a PhD in physics from Auburn University. E-mail him at jcrens@earthlink.net. Read more about Jack W. Crenshaw