chi-squared tests

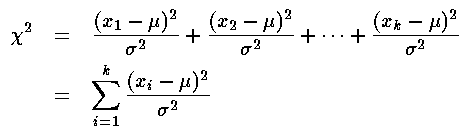
Consider a set of 10 measurements of leaf-size: {x1, x2, ..., x10}. where x1 is the size of the first leaf, etc. According to some expert, leaf sizes are supposed to be "normally" distributed with mean µ and standard deviation . Knowing all these numbers you could now calculate the quantity known as chi-square: .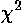

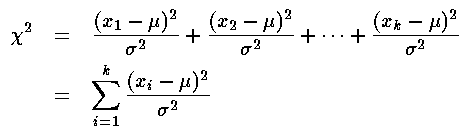
where in this case there are 10 x values, so k=10. (This formula says: find how each x deviates from the mean µ, square each difference, add up all the squared-differences and divide by the standard deviation squared.) More general versions of this formula would allow different means and standard deviations for each measurement.

Roughly speaking we expect the measurements to deviate from the mean by the standard deviation, so: |(xi-µ)| is about the same thing as 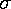. Thus in calculating chi-square we'd end up adding up 10 numbers that would be near 1. More generally we expect 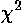to approximately equal k, the number of data points. If chi-square is "a lot" bigger than expected something is wrong. Thus one purpose of chi-square is to compare observed results with expected results and see if the result is likely.

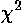X2: a version of to test expected distribution

Click here to calculate X2

In biology the most common application for chi-squared is in comparing observed counts of particular cases to the expected counts. For example, the willow tree (Salix) is dioecious, that is, like people (and unlike most plants) a willow tree will have just male or female sex organs. One might expect that half of the willows are male and half female. If you examine N willow trees and count that x1 of them are male and x2 of them are female, you will probably not find that exactly x1=½N and x2=½N. Is the difference significant enough to rule out the 50/50 hypothesis? We could almost calculate the chi-squared, but we don't know the standard deviation for each count. Never fear: most counts are distributed according to the Poisson distribution, and as such the standard deviation equals the square root of the expected count. Thus we can calculate X2:

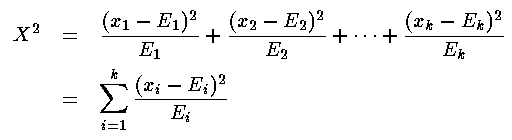
In our simple willow example there are just two cases so k=2, and the expected results are: E1=½N and E2=½N. Note that the Ei are generally not whole numbers even though the counts xi must be whole numbers. If there were more cases (say k cases), we would need to know the probability pi for each case and then we could calculate each Ei=piN, where N is determined by finding the total of the counts:

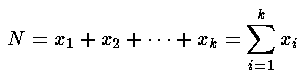
Finally it should be noted that the technical differences between a Poisson distribution and a normal distribution cause problems for small Ei. As a rule of thumb, avoid using X2 if any Ei is less than 5. If k is large this technical difficulty is mitigated.