Orbits in 2D
3D orbits here
Orbital Motion: motion of a particle with a 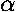 /r2 central force applied.
In intro physics the topic was the motion of planets under the influence of the Sun's gravitational
force...orbital mechanics. In quantum mechanics the topic is the motion of an electron under the influence of the
electrostatic attractive force of the nucleus...atomic physics. Equivalent equations for the force (and hence "the same"
as far a physics goes) but quite different distance scales.
/r2 central force applied.
In intro physics the topic was the motion of planets under the influence of the Sun's gravitational
force...orbital mechanics. In quantum mechanics the topic is the motion of an electron under the influence of the
electrostatic attractive force of the nucleus...atomic physics. Equivalent equations for the force (and hence "the same"
as far a physics goes) but quite different distance scales.
Planets move in ellipses with the Sun at one focus. Ellipses can be described in terms
of their semi-major axis, a, (basically the longest radius) and their eccentricity (basically
how squashed the ellipse is: e=0 is a circle, a fully squashed ellipse looks like
a line and has e=1).
r=a(1-e2)/(1+e cos(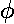 ));
rmin= a(1-e); rmax=a(1+e)
));
rmin= a(1-e); rmax=a(1+e)
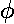 , the polar angle from closest approach is given the odd name:
true anomaly. The timing of the motion (i.e., when the planet or electron has
a particular
, the polar angle from closest approach is given the odd name:
true anomaly. The timing of the motion (i.e., when the planet or electron has
a particular 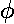 ) is a bit complex. The game is to express the
true anomaly (
) is a bit complex. The game is to express the
true anomaly (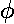 ) in terms of the eccentric anomaly (u)
and then find an expression relating time and the eccentric anomaly. For nearly
circular orbits it turns out that the true anomaly, the eccentric anomaly, and the
mean anomaly (
) in terms of the eccentric anomaly (u)
and then find an expression relating time and the eccentric anomaly. For nearly
circular orbits it turns out that the true anomaly, the eccentric anomaly, and the
mean anomaly (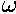 t) are all approximately
equal to each other. I apologize for this archaic nomenclature, but physics is stuck with these
names. Below find the geometric construction that relates the true anomaly and the eccentric anomaly,
the formula relating these two, and the formula relating time and the
eccentric anomaly.
t) are all approximately
equal to each other. I apologize for this archaic nomenclature, but physics is stuck with these
names. Below find the geometric construction that relates the true anomaly and the eccentric anomaly,
the formula relating these two, and the formula relating time and the
eccentric anomaly.
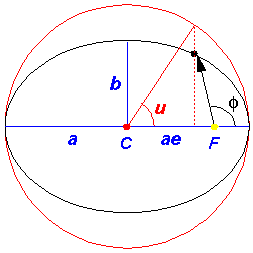
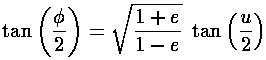
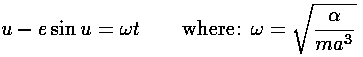
In the above picture, the yellow dot represents the Sun (or a nucleus); it is
at a focus (F) of the ellipse. The red parts of the diagram have to do with the geometric
construction for the eccentric anomaly which is measured from the center (C) of the
ellipse. There is nothing physically at the center of the ellipse, this is all just
part of a geometric construction. The blue parts of the diagram relate the semi-major
axis (a) and the distance between the ellipse center and the focus
(ae). The semi-minor axis, b, can be related to the
semi-major axis and the eccentricity:
b = a(1-e2)½
The black ellipse is the orbit of the particle, i.e., the set
of positions the particle will traverse during a period
(T=2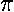 /
/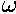 ).
).
It is most convenient to express the position of the particle in terms of u:
r = ( a(cos(u)-e),
a (1-e2)½ sin(u) )
In Mathematica we can easily display the orbit:
a=1; e=N[1/Sqrt[2]]
ParametricPlot[{a (Cos[u]-e),a Sqrt[1-e^2] Sin[u ]},{u,-Pi,Pi}]
But we have to
work to find the time dependence of the motion. Here we divide the period up
into 50 "tics". We must first create storage locations for our u
values and corresponding position vectors:
uu=Table[0,{51}]
rr=Table[{0,0},{51}]
Do[
uu[[i]]= u /. FindRoot[u-e Sin[u] == .04 Pi (i-26),{u,.04 Pi (i-26) }] ;
rr[[i,1]]=a (Cos[uu[[i]]]-e) ;
rr[[i,2]]=a Sqrt[1-e^2] Sin[uu[[i]]] ,
{i,51}]
The second part of the above is fairly complicated and has to do with solving
Kepler's equation:
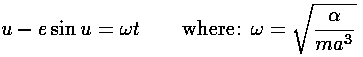
We seek u values that correspond to equally spaced times.
Thus we partition one full cycle:
-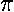 <
< 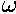 t <
t < 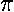
into little intervals:
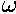 ti =
ti = 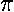 (i-26)/25
(i-26)/25
as i runs from 1 to 51,  ti
runs through one period. Finding the u that corresponds to each instant
ti, requires solving Kepler's equation. Kepler's equation cannot
be solved with algebra: we must numerically find the ui
that produces the proper ti...that's what the
FindRoot is doing. Once we have found our ui
that satisfies Kepler's equation, we substitute it in ("/.") for
u and save it in uu[[i]]. From uu[[i]] we can calculate
the corresponding
ti
runs through one period. Finding the u that corresponds to each instant
ti, requires solving Kepler's equation. Kepler's equation cannot
be solved with algebra: we must numerically find the ui
that produces the proper ti...that's what the
FindRoot is doing. Once we have found our ui
that satisfies Kepler's equation, we substitute it in ("/.") for
u and save it in uu[[i]]. From uu[[i]] we can calculate
the corresponding
rx=rr[[i,1]]
ry=rr[[i,2]]
We can then plot these points:
ListPlot[rr]
We can combine the dot-plot with the orbital curve with a Show
(say the ParametricPlot was Out[6] and the
ListPlot was Out[10]:
Show[%10,%6,AspectRatio->Automatic]
If you want you can figure out the various  i:
i:
pp=Table[0,{51}]
Do[
pp[[i]]=N[2 ArcTan[ Cos[uu[[i]]/2], Sqrt[(1+e)/(1-e)] Sin[uu[[i]]/2] ] ],
{i,51}]
The velocity vector is, of course, changing as the position vector is changing.
The set of velocities the particle will have during a period is called the
hodograph; it's just like an orbit, but for velocity rather than position.
The hodograph is surprising: it's just a circle, but the center of the circle is
not v=0.
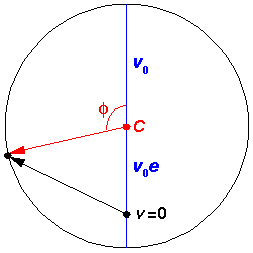
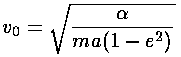
Note that at closest approach to the "Sun" (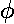 =0) the speed is a maximum
and the velocity points in the y direction, whereas at the far point
(
=0) the speed is a maximum
and the velocity points in the y direction, whereas at the far point
(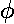 =180°) the speed is a minimum
and the velocity points in the -y direction. As the eccentricity
approaches 1, the maximum speed gets arbitrarily large and the minimum speed
approaches zero.
=180°) the speed is a minimum
and the velocity points in the -y direction. As the eccentricity
approaches 1, the maximum speed gets arbitrarily large and the minimum speed
approaches zero.
We could now use Mathematica to make plots of the velocity vector:
vxy=Table[{-Sin[pp[[i]]],Cos[pp[[i]]]+e},{i,51}]
ListPlot[%,AspectRatio->Automatic]
ParametricPlot[{-Sin[u ],(Cos[u]+e) },{u,-Pi,Pi}]
Show[%,%%,AspectRatio->Automatic]
The above figures have been drawn with a rather large eccentricity: e=.707.
For eccentricities
similar to those of the planets it would be hard to distinguish the elliptical orbit from
a circle (although for some planets--like Mars--the position of the Sun would look
noticeably "off-center"...because the Sun is at a focus rather than the center).
If the (attractive) radial force is given by:
Fr=-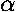 /r2, the
potential energy is U(r)=-
/r2, the
potential energy is U(r)=-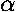 /r,
so that the minus derivative of U is
the force. Notice that just like the spring
(U(x)=½k x2, which also attracts to the origin), the potential
energy is ever smaller as you approach the origin. Unlike the spring, this potential energy is
numerically negative (i.e., U(r)<0).
That is a result of our choice of additive constant. For the spring we choose the potential
to be zero at the origin, forcing the potential to be arbitrarily big as x approaches infinity.
For this problem we take the potential energy to be zero as r approaches infinity, so the potential
at the origin must be infinitely less, i.e., negative infinity.
The seemingly over-complex geometric description of motion:
/r,
so that the minus derivative of U is
the force. Notice that just like the spring
(U(x)=½k x2, which also attracts to the origin), the potential
energy is ever smaller as you approach the origin. Unlike the spring, this potential energy is
numerically negative (i.e., U(r)<0).
That is a result of our choice of additive constant. For the spring we choose the potential
to be zero at the origin, forcing the potential to be arbitrarily big as x approaches infinity.
For this problem we take the potential energy to be zero as r approaches infinity, so the potential
at the origin must be infinitely less, i.e., negative infinity.
The seemingly over-complex geometric description of motion:


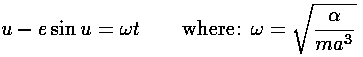
can, with some work, be seen to solve the equation of motion:
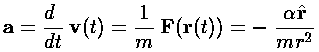
Start by noting that the velocity vector is made of a constant
vector (ev0j)
added to the red rotating vector. Taking the time derivate removes
the constant from consideration, so the acceleration vector must
be tangent to the circle--i.e., rotated 90° from the red radial
vector, which is itself rotated 90° from r (note
that the zero for 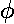 was the x-axis for
the orbit and the y-axis in the hodograph). Thus
the acceleration vector is in the right direction: -r.
The magnitude of the acceleration vector is just:
was the x-axis for
the orbit and the y-axis in the hodograph). Thus
the acceleration vector is in the right direction: -r.
The magnitude of the acceleration vector is just:
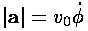
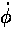 is related to the
(constant) angular momentum (L) [which we can
evaluate for example, at the near point].
is related to the
(constant) angular momentum (L) [which we can
evaluate for example, at the near point].
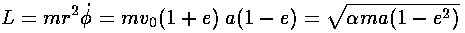
Solving the above for 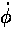 and substituting
into our equation for the magnitude of the acceleration vector, yields:
and substituting
into our equation for the magnitude of the acceleration vector, yields:
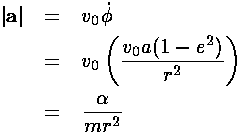
Note in passing that if the angular momentum is zero,
then e=1. The circular orbits (e=0)
have the maximum possible angular momentum for a given semi-major axis
a, that is for a given energy E because
there is a simple relation between the semi-major axis a
and E:
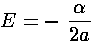
Note that the energy is negative; the positive kinetic energy
equals (on average) one half the absolute value of the potential energy
(the Virial theorem again!) and the result is that the total energy
is ½ the average potential energy.
Here is another way of presenting the results:
plots displaying the position of the particle on
the orbit and the velocity of the particle on the
hodograph at a series of equally spaced times.
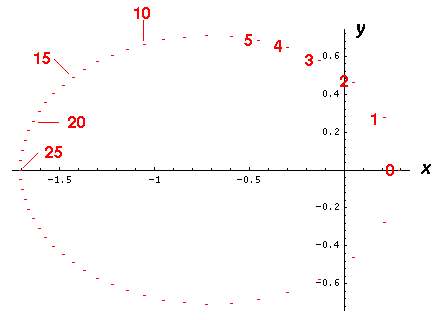
The above is a plot of the (x,y) location of
a electron (or planet) at successive increments of time (tics)
Note the when the electron (planet) is close to the nucleus (or Sun),
the particle seems to move a great distance between tics, whereas
when the particle is is far from the origin, it seems to move
only a little between tics. This is exactly what you would
expect for a particle conserving angular momentum (i.e., following
Kepler's second law of constant areal velocity).
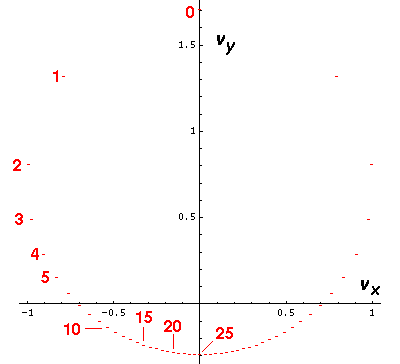
The above is a plot of the (vx,vy)
velocity of
a electron (or planet) at successive increments of time (tics)
Note the when the electron (planet) is close to the nucleus (or Sun)
(e.g., near tic 0)
the velocity seems to change quite a bit between tics, whereas
when the particle is is far from the origin
(e.g., near tic 25), the velocity seems to change
only a little between tics. This is exactly what you should expect
for a 1/r2 force.
Note that the motion is confined to a plane so we can display
the results on a flat screen.
If we ignore the angular part of the motion, we can make plots of the
the radial velocity vs. time (in tics),
the distance from the origin (r) vs. time, and
the speed (v) vs. time:
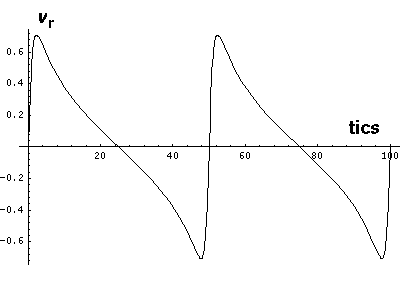
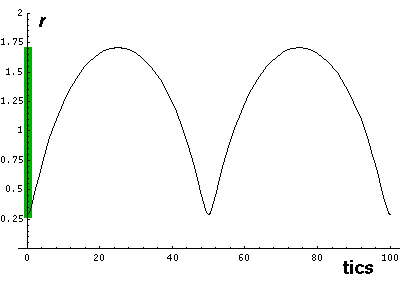
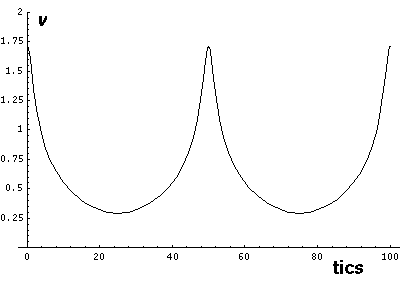
Note that r seems to "bounce" off the minimum radius
rmin. The motion is in fact quite similar to the
bouncing falling ball. Here vr changes quickly
(but not instantaneous) between negative (falling) and positive (rising)
values. The green area on the r plot shows the classically
allowed region.
Note that while r does range between two values:
rmin= a(1-e) &
rmax=a(1+e),
these turning points are a bit different from 1-d
turning points as v is never zero.
We can, however, threat our 3-d (reduced to 2-d) motion
as a 1-d motion in an
effective potential (see for example, Marion p.301, Barger & Olsson p.138,
Goldstein p.61) which includes the centrifugal potential:
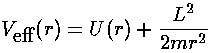
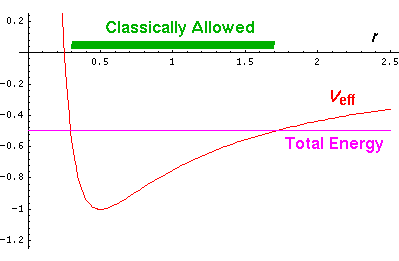
The above diagram plots various the energies involved
as a function of r. The
line representing "Total Energy" is flat, because total energy is
conserved (i.e., is constant).
Total energy is the sum of
kinetic energy and potential energy. We can decompose
kinetic energy (½mv2) into two pieces
by using the Pythagorean theorem to decompose v2 into the sum of two terms:
radial velocity squared (vr2)
and the component of velocity perpendicular to r
("transverse" velocity) squared. The
"transverse" kinetic energy, can be calculated from the
angular momentum and r...the result is the centrifugal potential.
The centrifugal potential has
been added to the 1/r potential; the result is plotted
in red.
Thus total energy is the sum of the effective potential and
the "radial" kinetic energy. At the turning points there
is zero "radial" kinetic energy, and the
radial velocity is zero (i.e., the particle is no longer moving in
or out: r is either at a minimum or a maximum).
We note that for orbital motion, the time to complete
a radial oscillation :
(i.e., rmin rmax
rmax rmin)
is also the time it takes to go around the Sun
(i.e., for
rmin)
is also the time it takes to go around the Sun
(i.e., for  to increase by 2
to increase by 2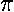 ).
).
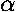 /r2 central force applied.
In intro physics the topic was the motion of planets under the influence of the Sun's gravitational
force...orbital mechanics. In quantum mechanics the topic is the motion of an electron under the influence of the
electrostatic attractive force of the nucleus...atomic physics. Equivalent equations for the force (and hence "the same"
as far a physics goes) but quite different distance scales.
/r2 central force applied.
In intro physics the topic was the motion of planets under the influence of the Sun's gravitational
force...orbital mechanics. In quantum mechanics the topic is the motion of an electron under the influence of the
electrostatic attractive force of the nucleus...atomic physics. Equivalent equations for the force (and hence "the same"
as far a physics goes) but quite different distance scales.
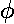 ));
rmin= a(1-e); rmax=a(1+e)
));
rmin= a(1-e); rmax=a(1+e)
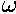 t) are all approximately
equal to each other. I apologize for this archaic nomenclature, but physics is stuck with these
names. Below find the geometric construction that relates the true anomaly and the eccentric anomaly,
the formula relating these two, and the formula relating time and the
eccentric anomaly.
t) are all approximately
equal to each other. I apologize for this archaic nomenclature, but physics is stuck with these
names. Below find the geometric construction that relates the true anomaly and the eccentric anomaly,
the formula relating these two, and the formula relating time and the
eccentric anomaly.

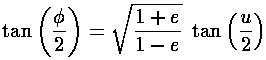
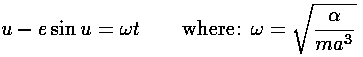
 /
/
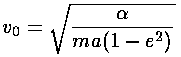
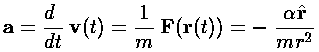
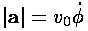
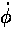 is related to the
(constant) angular momentum (L) [which we can
evaluate for example, at the near point].
is related to the
(constant) angular momentum (L) [which we can
evaluate for example, at the near point].
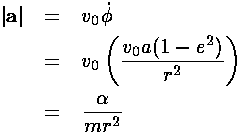
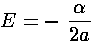


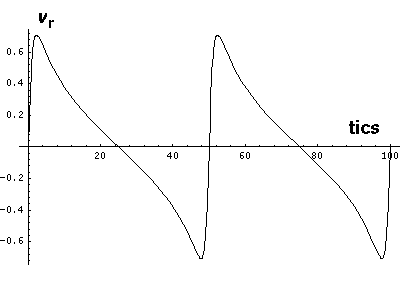


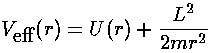

 rmax
rmax