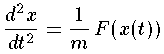
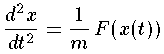
In quantum mechanics the primary aim is to solve the time independent Schrödinger's equation to find the probability amplitude (i.e., the wavefunction) as a function of position.
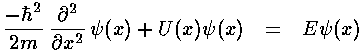
Note again the huge shift between classical mechanics and quantum mechanics: what was the dependent variable in classical mechanics (x) has become the independent variable; what was the independent variable (t) has disappeared. It turns out energy (E) is more measurable than motion, hence energy has replaced time as the most important variable.
Almost any "real" problem in classical mechanics (e.g., a real cannon ball flying through the Earth's atmosphere) is so complex that it cannot be solved using paper-and-pencil methods: the differential equation must be solved "numerically" using a computer. Quantum mechanics only makes things more difficult. Only the simplest examples have "analytical" solutions (i.e., the answer can be written down using "well known" functions). The purpose of these textbook problems is to provide examples where all the dependencies are explicit so that they are available for play/understanding.
If a problem has an analytical solution, say,
=f(x)
where f(x) is some "well-known" function, consider the
consequences. Just about every "well-known" function requires
that its argument be dimensionless. (I can think of only two
counterexamples.) Thus =sin(x),
or =exp(-x2) cannot be
proper answers if x has the units...you cannot take
the sine of 1 meter, nor have a power that is 1 square-meter.
Thus answers must be of the form:
=f(x/L)
where L "sets the scale" of the problem, i.e., has units that cancel those of x. Thus the first point-of-attack on any physics problem is to determine how you could form quantities like L that allow you to form dimensionless quantities like x/L.
The square-well problem is so simple that use of dimensioned coordinates
is not too burdensome and and one can instead consistently
write formulas that have explicitly x/L etc. (or more commonly:
kx where k=
n/L).
[Remember: L=2a is the full width of our square well.]
What makes the quantum mechanics problem so simple is that the above potential U(x) essentially does not depend on x. (That is U(x) is constant except for jumps at specified x.) Thus almost everywhere we can combine the eigenenergy E with the constant potential U0, producing a familiar differential equation.
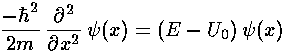
Note: Since the potential is zero "inside" our square well, U0 would disappear there.
Schrödinger's
equation has the constant: 
2/2m=A.
A has the units of
energy·length2. Using L as our unit of
length,
e=A/L2
has the units of energy.
It is worthwhile to calculate the numerical value of these scales
for some typical systems:
| System | particle | length scale | energy scale |
|---|---|---|---|
| Atom | electron | 1 Å | 4 eV |
| Benzene circumference | electron | 9 Å | .05 eV |
| quantum dot | electron | 0.1 µm | 4 µeV |
| Nucleus | neutron proton | 10 fm | 0.2 MeV |
(Note 1 Å=10-10m, 1 fm = 10-15m.)