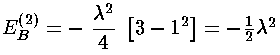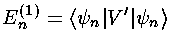
In first order perturbation theory the small shift in energy is given by the following formula:
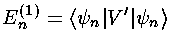
That is that the first order shift in the energy of the
nth energy eigenfunction
(En(1)) is just the expectation value
of the additional potential (V') using the nth
energy eigenfunctions ( n)
(i.e., the shift in energy is just the
average value of the potential for the unperturbed eigenfunction).
n)
(i.e., the shift in energy is just the
average value of the potential for the unperturbed eigenfunction).
Calculating the second order shift in energy requires a bit more work:
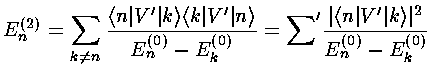
The (unnormalized) perturbed wavefunction ( ) is given by:
) is given by:
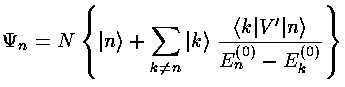
where |k>= k are the unperturbed wavefunctions.
k are the unperturbed wavefunctions.
Consider then the (fairly bogus) example of a small additional (1-d) spring force:
V(x)=½kx2(1+ )
)
V'(x)=½kx2
It's "fairly bogus" because we can exactly solve this problem (since it's just a slightly stronger spring problem and we've solved the spring problem), but thats the point: we can then compare the perturbation theory approximation to the exact answer.
The exact answer just amounts to a shift in our energy unit e.
En=(2n+1)e
e=½(k/m)½
(1+ )½=1 + ½
)½=1 + ½ -
-  2/8
2/8
Before we can calculate the second order shift we should calculate the first order shift. Thus we need to find the following integral:
<n|x'2|n>
The virial theorem would give us that integral, but instead lets do it using the recursion relations.
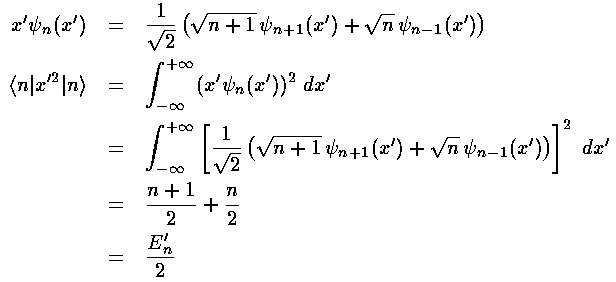
Thus the first order shift in energy is itself proportional to the unperturbed energy:
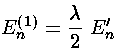
Calculating a second order shift looks to be quite difficult: an infinite number of integrals must be performed and then we must sum an infinite number of terms. Luckily all of the integrals can be calculated via the recursion relation and via orthogonality and almost all of them are zero.
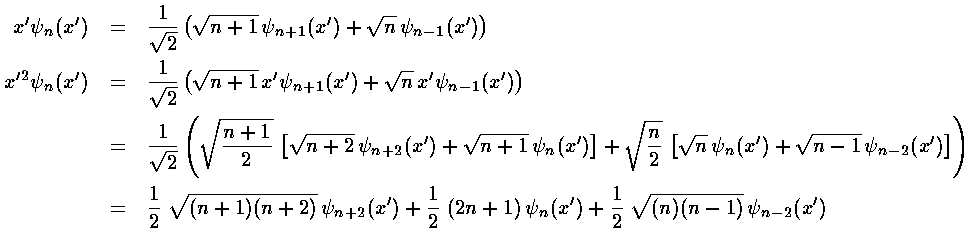
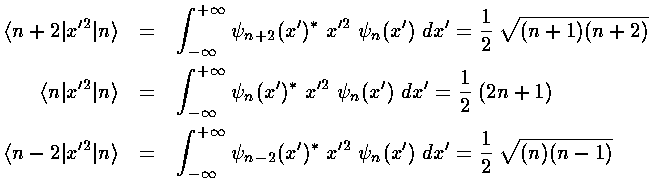
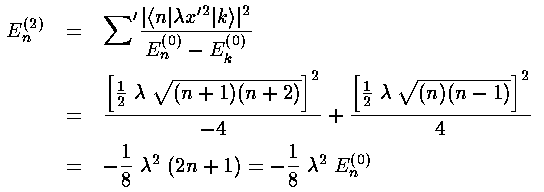
This results exactly reproduces what we expected from our Taylors
expansion of (1+ )½ shown above.
)½ shown above.
The solution to the problem is to find a new basis for the degenerate subspace such that <k|V'|n> is zero. For example, in the 3-d oscillator at E'=7 there are 6 degenerate states (5 d [l=2] states and 1 s [l=0] state). Any linear combination of these states also solves Schrödinger's equation with E'=7. With work, we can find six new wavefunctions (just linear combinations of the old |nrlm>) which (a) span the degenerate subspace (i.e., any function that can be formed from a linear combination of the |nrlm> can be formed from a linear combination of our six new wavefunctions) and (b) the perturbation will not connect any distinct pair of our six wavefunctions (i.e., <k|V'|n>=0 for different states |n> and |k>).
The new basis will be found by finding the eigenvectors of the matrix for V' on the degenerate subspace. So we need to begin by finding all 36 3-d integrals:
<nrlm|V'|n'rl'm'>
Our example perturbing potential:
V'= (x2-y2)
can be usefully expressed in terms of the spherical harmonics: Y2 ±2
(x2-y2)
can be usefully expressed in terms of the spherical harmonics: Y2 ±2
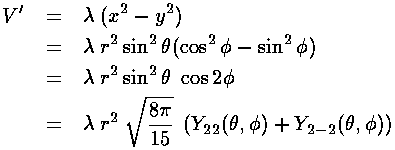
The Ylm( ,
, )
part of the needed 36 integrals is easily found via the Wigner-Eckart
Theorem (Schiff p.223, many details in Edmonds Angular Momentum in
Quantum Mechanics)
)
part of the needed 36 integrals is easily found via the Wigner-Eckart
Theorem (Schiff p.223, many details in Edmonds Angular Momentum in
Quantum Mechanics)
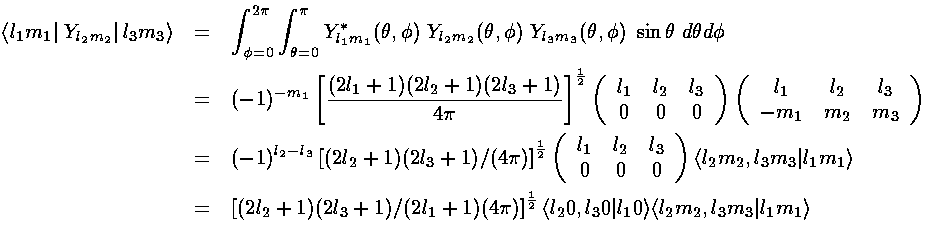
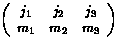 are called Wigner's 3-j symbols
and are essentially symmetric versions of the Clebsch-Gordan coefficients
(<j1m1,j2m2|j3m3> a.k.a., vector coupling coefficients). (3-js should not be confused
with Racah 6-j symbols
are called Wigner's 3-j symbols
and are essentially symmetric versions of the Clebsch-Gordan coefficients
(<j1m1,j2m2|j3m3> a.k.a., vector coupling coefficients). (3-js should not be confused
with Racah 6-j symbols 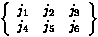 which are involved
in "recoupling" of angular momentum.) Mathematica
knows about all of the above functions; Abramowitz and Stegun (p.1006)
have formulas for some low j Clebsch-Gordan coefficients;
the particle data handbook has a nice table of
j<=2 Clebsch-Gordan coefficients (click here
for a printable postscript version of their table). Here are some basic properties
of 3-j symbols:
which are involved
in "recoupling" of angular momentum.) Mathematica
knows about all of the above functions; Abramowitz and Stegun (p.1006)
have formulas for some low j Clebsch-Gordan coefficients;
the particle data handbook has a nice table of
j<=2 Clebsch-Gordan coefficients (click here
for a printable postscript version of their table). Here are some basic properties
of 3-j symbols:
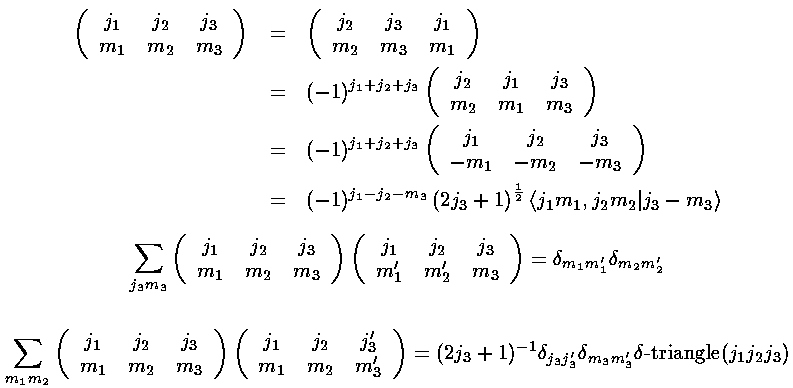
The key point in these formulas for the Ylm integrals is that
<l1m1|Yl2m2|l3m3>
is zero unless the m's properly add (i.e., m1=m2+m3)
and the l's satisfy the triangle property
(|l3-l2|<=l1<=l3+l2).
In addition there is a parity constraint hidden in the reduced matrix element
(i.e., the zero-m 3-j). Under inversion,
Ylm (-1)lYlm.
The integrand must be overall even to produce a non-zero result, hence:
l1+l2+l3 must be even.
(-1)lYlm.
The integrand must be overall even to produce a non-zero result, hence:
l1+l2+l3 must be even.
In this example, our basis states are l=2 (5 |lm> states: |22>, |21>, |20>, |2-1>, |2-2>) and l=0 (|00>) and the perturbing potential V' is essentially Y2 2+Y2 -2. Using the above result for Ylm integrals only the following matrix elements are non-zero (i.e., the potential "connects" only the listed states)
<22|V'|20> & <22|V'|00>
<20|V'|2-2> & <00|V'|2-2>
<21|V'|2-1>
A moment's thought should convince you that the first two rows of matrix elements are related as Y*lm=(-1)mYl-m. Thus <20|V'|2-2> is exactly the same integral as <22|V'|20>.
Note that all diagonal matrix elements (i.e., expectation values) are zero as
Y*lmYlm is cylindrically symmetric
(i.e.,  -symmetric) so <x2>=<y2>
and hence <x2-y2>=0. So simple-minded application
of first order perturbation theory would yield unchanged energy levels
(which is, of course, wrong).
-symmetric) so <x2>=<y2>
and hence <x2-y2>=0. So simple-minded application
of first order perturbation theory would yield unchanged energy levels
(which is, of course, wrong).
Note that the even-m basis states are totally unconnected to the odd-m basis states, so our 6×6 matrix for V' has two blocks placed along the diagonal (with zero connection): 2×2 matrix of odd-m basis states (which we order: |21>,|2-1>) and 4×4 matrix of even-m basis states (which we order: |22>, |20>, |00>, |2-2>)
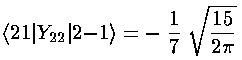
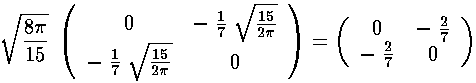
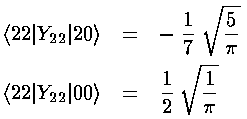
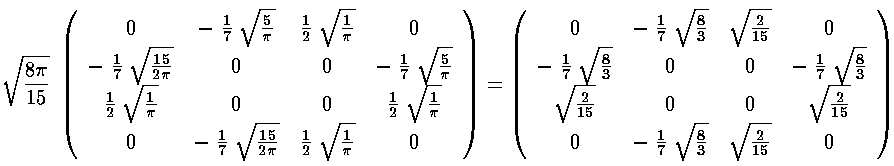
The radial part of the integral must now be tackled. The angular part of the perturbation x2-y2 ended up in Y2 2+Y2 -2, the radial part is r2, so we need to evaluate integrals like:
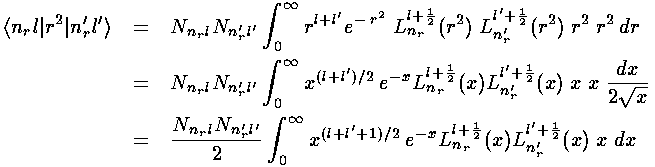
In the case l=l' we have exactly the "weighting function"
xl+½e-x needed
for the orthogonality of the Laguerre polynomials (i.e.,
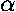 =l+½). The recursion relation for
the Laguerre polynomials can then be used to convert
x Ln(x) into a sum of three Ls,
orthogonality then makes the resulting integrals easy.
=l+½). The recursion relation for
the Laguerre polynomials can then be used to convert
x Ln(x) into a sum of three Ls,
orthogonality then makes the resulting integrals easy.
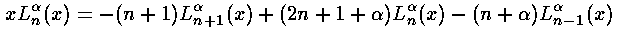
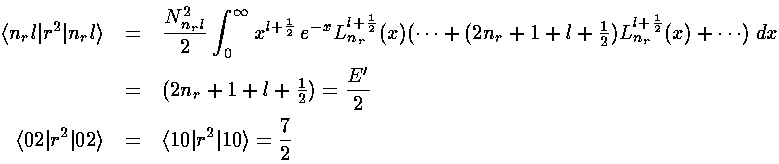
Note that we could have also derived this result via the Virial Theorem.
The other needed case is l=l'+2. The strategy here is to steal one x from r2 and another from the weight function and to re-express x2Ll+½ in terms of Ll'+½ through a double use of the formula (Abramowitz & Stegun 22.7.31 or Szegö 5.1.14):
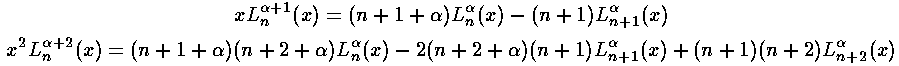
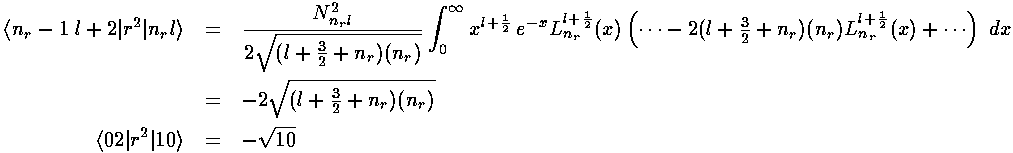
Multiplying our r integral result by our  ,
, integral result gives us the required matrix elements. Here are the results:
integral result gives us the required matrix elements. Here are the results:
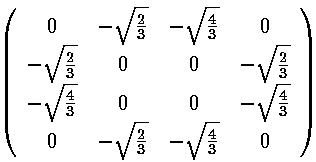
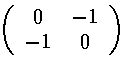
Mathematica's Eigensystem[m] command gives us the eigenvectors and eigenvalues of the matrix m. Here are the results.
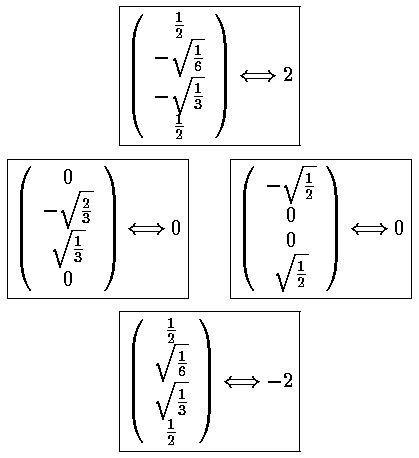
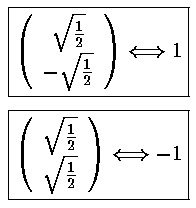
Thus the 6 degenerate E'=7 states "split" into states with the following
energies: E'=7+2 , E'=7+
, E'=7+ ,
E'=7 (doubly degenerate), E'=7-
,
E'=7 (doubly degenerate), E'=7- , and
E'=7-2
, and
E'=7-2 .
.
This result can be compared to the exact result since the problem is still exactly
the sum of three oscillators: kx=(1+ )k;
ky=(1-
)k;
ky=(1- )k; and
z is unchanged: kz=k.
The resulting eigenenergy is the sum of the x, y, and z
eigenenergies:
)k; and
z is unchanged: kz=k.
The resulting eigenenergy is the sum of the x, y, and z
eigenenergies:
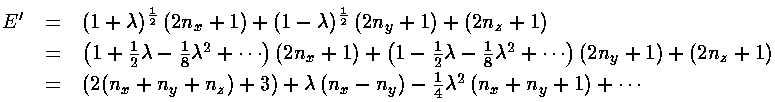
In the unperturbed system there are 6 combinations that produce E'=7: (nx,ny,nz)= (2,0,0), (0,2,0), (0,0,2), (0,1,1), (1,0,1), and (1,1,0). With the added perturbation these states sort themselves out (high to low energy) as: (2,0,0), (1,0,1), [(1,1,0), (0,0,2), degenerate in first order], (0,1,1), (0,2,0). The resulting first-order energies are exactly as produced in perturbation theory.
For the four states that became non-degenerate in first-order, we can go on to find their second order correction in the usual way and compare the calculation to the exact results shown above. For the remaining degenerate pair more work is needed to find the "right" linear combination, see Schiff p.250.
Let us focus on the second order correction of a particular state: the
E'(1)=+ state (|021>-|02-1>)/2½=|B>.
In order to calculate the second order shift we need to find an infinite number
of integrals: <k|V'|B> where k
represents any nrlm state. We don't have to worry
about states in the E'=7 set we constructed above: V'
does not connect them with |B> as the eigenvectors are orthogonal.
Because of the angular integral we need only consider states with
l=2,4 and m=-3,-1,1,3 (matrix elements with all other
states are zero). For l=2, the r integral leads to the
Laguerre orthogonality integral; recursion on xLnr
produces polys of degree nr-1,nr,nr+1,
one of which must match the nr=0 of |B>. Thus only
nr=1,l=2,m=±1 can connect with |B>.
For l=4, use of
state (|021>-|02-1>)/2½=|B>.
In order to calculate the second order shift we need to find an infinite number
of integrals: <k|V'|B> where k
represents any nrlm state. We don't have to worry
about states in the E'=7 set we constructed above: V'
does not connect them with |B> as the eigenvectors are orthogonal.
Because of the angular integral we need only consider states with
l=2,4 and m=-3,-1,1,3 (matrix elements with all other
states are zero). For l=2, the r integral leads to the
Laguerre orthogonality integral; recursion on xLnr
produces polys of degree nr-1,nr,nr+1,
one of which must match the nr=0 of |B>. Thus only
nr=1,l=2,m=±1 can connect with |B>.
For l=4, use of 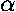 -recursion to reduce x2L for l=4
to l=2 yields new l=2 polynomials with degree:
nr,nr+1,nr+2 one of which must match
the nr=0 of the |B> state. Thus only
nr=0,l=4,m=±1,±3. Note that
each of the six states we've found that connect with |B> have
E'=11. This allows us to use a neat trick, and thereby avoid doing
any of the above integrals. The starting point is to realize that since
the energy denominator is constant (-4) for all the non-zero terms in the sum,
we can pull that constant outside of the sum. Finally we use completeness: that
the sum over all states is the unit operator.
-recursion to reduce x2L for l=4
to l=2 yields new l=2 polynomials with degree:
nr,nr+1,nr+2 one of which must match
the nr=0 of the |B> state. Thus only
nr=0,l=4,m=±1,±3. Note that
each of the six states we've found that connect with |B> have
E'=11. This allows us to use a neat trick, and thereby avoid doing
any of the above integrals. The starting point is to realize that since
the energy denominator is constant (-4) for all the non-zero terms in the sum,
we can pull that constant outside of the sum. Finally we use completeness: that
the sum over all states is the unit operator.
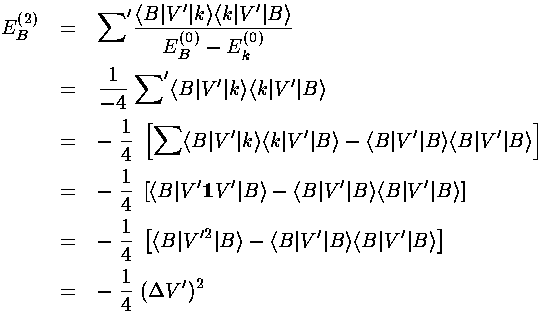
<B|V'|B> = 
The angular integral part of <B|V'2|B> gives
4/21; the radial part 63/4, so the result is 3 2.
2.
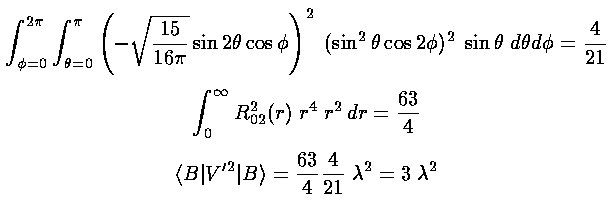
Putting the results together we find the same second order correction calculated
(much easier) via the xyz separation: ½ 2.
2.