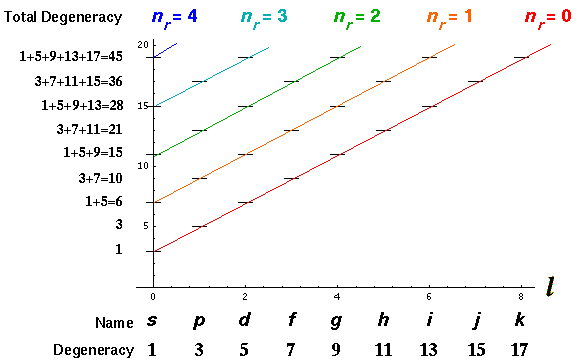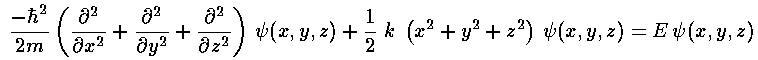
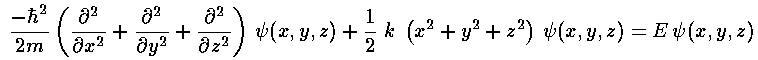
Proceeding exactly as before we have the dimensionless form
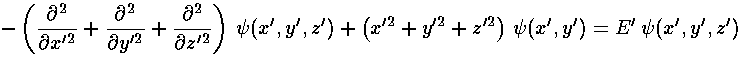
Since the total Hamiltonian can be written as the sum of three Hamiltonians (one just in x', the second just in y', and the third just in z'; each Hamiltonian has the same form as a 1-d oscillator), the solution is just the product of three 1-d oscillator wavefunctions (one just in x' the second just in y', the third just in z'):
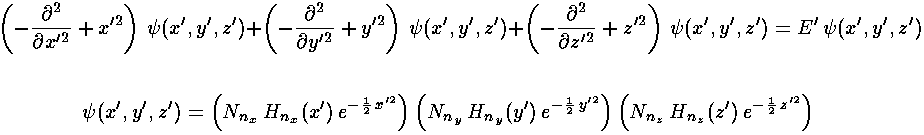
with E'= (2nx+1 + 2ny+1+ 2nz+1), i.e., the energy is just the sum of the "x" E', the "y" E' and the "z" E'. Note we again have degeneracy (different wavefunctions with the same energy): e.g., nx=1 & ny=0 & nz=0; nx=0 & ny=1 & nz=0; nx=0 & ny=0 & nz=1; all have E'=5.
Since the problem is rotationally symmetric rather
than square-symmetric, it makes more sense to use a coordinate
system that reflects the symmetry in the problem. Hence,
I'd like to solve this problem is spherical coordinates
(r'-
-
).
Changing coordinates changes the Schrödinger's equation to:
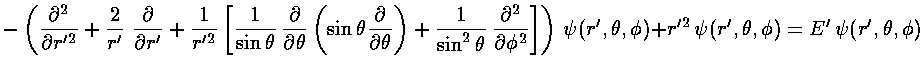
The stuff in the square brackets (with the overall minus sign) is the (dimensionless) angular momentum squared operator: L'2. The eigenfunctions of this operator are degenerate, so there is a choice to make in defining the basis states. In physics folks conventionally use the Ylm, which are simultaneously eigenfunctions of both L'2 and L'z:
L'2 Ylm = l(l+1) Ylm
L'z Ylm = m Ylm
Chemists not uncommonly use a different basis which has the advantage that the functions are real, but the disadvantage that they do not display spherical symmetry.
The probability density Ylm*Ylm
is independent of ("cylindrically symmetric" for a cylinder
whose axis is aligned with the z axis) so we only need to concern
ourselves with their dependence on . As you would expect
if the angular momentum is aligned with the z axis (so m=l)
the probability should mostly be in the x-y plane, i.e.,
=
/2=90°. Below is
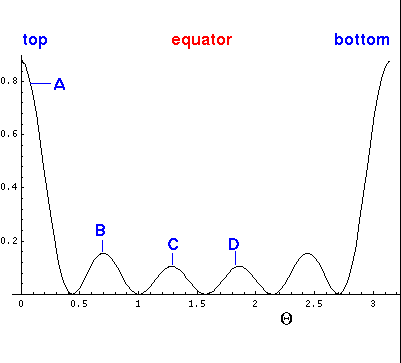
a plot of the probability density for l=m=5.
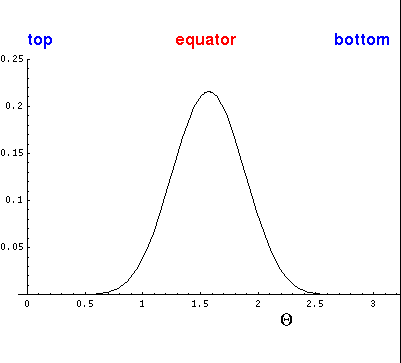
Here is the corresponding plot just as a function of .
On the other hand, if m=0, the angular momentum vector must be
in the x-y plane and the particle must be moving perpendicular
to the angular momentum vector and hence in part in the
z direction. For example, if L~i
(i.e., the angular momentum vector is in the x direction), we expect
motion to be in the y-z plane. The m=0 solutions
are essentially superpositions of all possible orientations of L
in the x-y plane. What survives the superposition is:
(1) a big amplitude on the z-axis where all orientations
contribute, (2) oscillation
(motion) in and (3) uniform distribution in
.
Below is
a plot of the probability density for l=5, m=0.
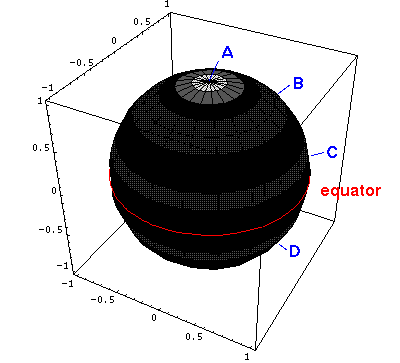
Here is the corresponding plot just as a function of .
(Here is a bit more information about the Ylm and other choices.)
Seeking a solution where the dependence on r' factors
with all the ,
dependence in Ylm ("separation of variables"),
i.e., 
=R(r')Ylm
we find:
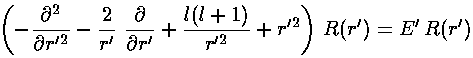
As usual we have to work a bit to solve for the r' wavefunction. Start by seeing how the equation must work for large r'. The only term that has a chance of matching the ever growing r'2 is the two-derivative term. Just as in the 1-d oscillator, an approximate cancellation requires exp(-½r'2) behavior.
For small r' only the derivative terms have a chance to match the ever growing l(l+1)/r'2 term. If we try a power-law solution r'n
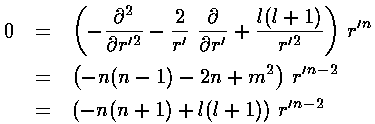
we find n=l or n=-(l+1); the former is not singular as r' nears 0
Factoring out all the required behavior for large and small r', we hope to find a simple function (polynomial with luck) F(r') that contains the behavior for intermediate r'.
=r'l
exp(-½r'2) F(r')
So the next step is to rewrite Schrödinger's equation for F(r'). In what follows I've decided to call r' just r for notational ease.
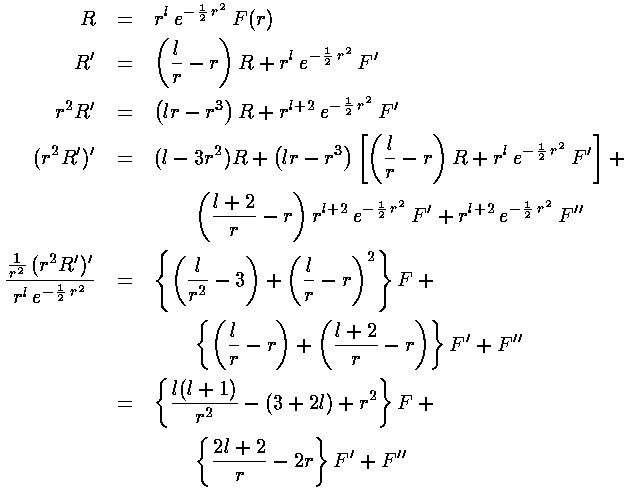
So:
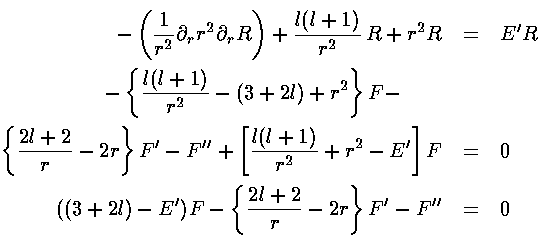
If we now try to write F as a polynomial:
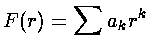
we can plug the polynomial form into the differential equation:
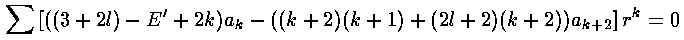
The result is a two term recursion relation (i.e., the result has just two as so, for example, given a0 we can calculate a2, from which we can calculate a4, etc. until we're done.)
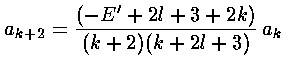
Note that the the recursion relation connects even k to even k. Since a0 may not be zero (as if it were we'd factor out r, thus increasing the rl term to rl+1). the polynomials will have only even terms. Thus we write our even k=2i, where i is an integer.
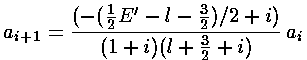
It turns out that the polynomial must end if the
wavefunction is to be normalizable. One can show that the non-terminating
sum gets at least as big as exp(+r2), so
instead of going to zero for large r gets
big like: exp(+r2/2). The only way the sum can end is if
the numerator of the recursion relation is zero, i.e., if
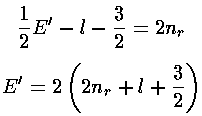
Thus if E'=4nr+2l+3 then ai+1=0 for i=nr (and hence all further as are zero) and the highest power of r2 in the polynomial is nr.
Note that if we had tried for a polynomial solution for
itself (rather than factoring out the
rl exp(-r2/2) first),
we would get an (unsolvable) three term recursion relation.
The polynomials we have been calling F are Laguerre polynomials (see for example, Abramowitz & Stegun, §22 p. 771 or Szegö Ch.V).
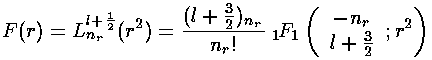
Here is the overall solution:
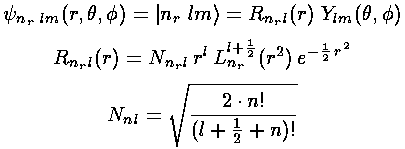
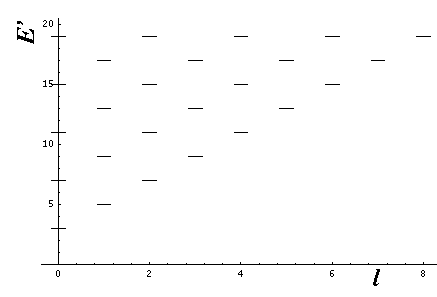
Here is a fancier display of energy levels as a function of l
