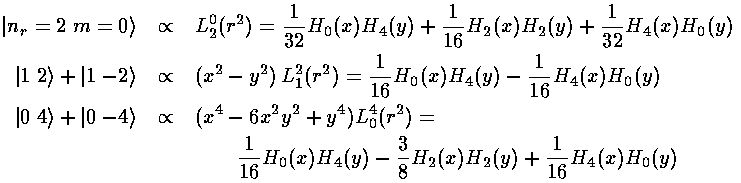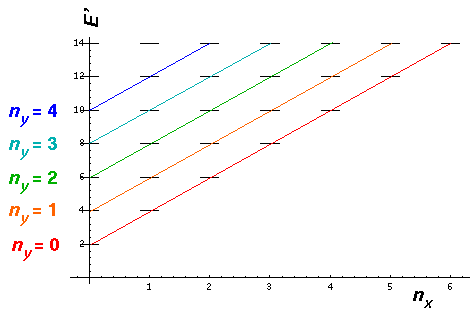
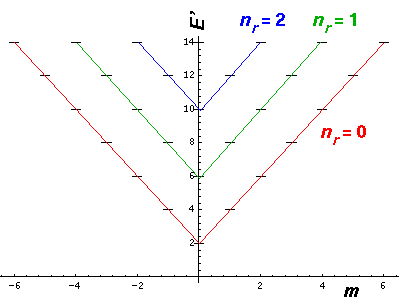
Here are the collection of energy levels produced by solving
the 2-d oscillator in the r-
coordinate system:
The wavefunctions for these levels look different:
the x-y wavefunctions have square symmetry while the
r- wavefunctions have circle-symmetry.
Nevertheless, notice that for any value of E' the number
of levels ("degeneracy") is the same in either system. For example,
E'=10 includes 5 |nrm> wavefunctions:
|0,-4>, |1,-2>, |2,0>, |1,2>, and |0,4> or includes 5
|nxny> wavefunctions:
|0,4>, |1,3>, |2,2>, |3,1>, and |4,0> .
In fact the set of functions spanned by forming all possible
linear combinations of the 5 |nrm> wavefunctions
is identical to that formed by all possible
linear combinations of the 5 |nxny>.
In particular any |nrm> wavefunction
can be expressed as a linear combination of the co-degenerate
|nxny> wavefunctions
(and visa-versa). The degenerate x-y wavefunctions
and the r- wavefunctions are thus
different basis vectors for the same subspace.
Here is a start on finding the sum of |nxny> which equals any |nrm> for E'=10.
