SHM p.7

Some Details on QM Oscillation

As previously stated, energy eigenfunctions have position probabilities that do not depend on time (although the energy eigenfunctions themselves do have a [complex] time dependence). Thus to see motion (i.e., positions that depend on time), we must not be in a energy eigenfunction. The alternative is to be in several energy eigenfunctions, i.e., to be in a superposition of energy eigenfunctions. Thus the idea is to create a superposition of energy eigenfunctions which initially has a narrow range of position possibilities, and watch that range of position possibilities move.

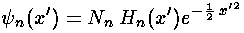
The game then is a version of Fourier analysis: producing a sum-of-eigenfunctions that adds up to a given function. Orthogonality is what makes this easy; in particular, that our energy eigenfunctions are mutually orthogonal.

Our normalized energy eigenfunctions are gaussian-damped Hermite polynomials:

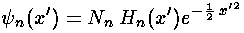
where N_n is given by:

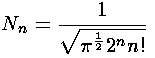
These eigenfunctions are orthogonal:

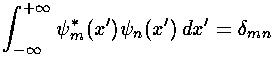
So if we try to express a given function f(x') in terms of a sum of these functions:

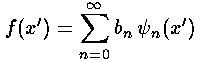
orthogonality allows us to solve for the b_n:

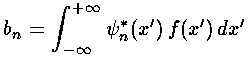
In this particular example, I choose f(x') to have the shape of the n=52 state, but with f(x')=0 for x'<~9.4 (The first zero of the wavefunction is at ~9.4, thus this f(x') is the solution to the Schrödinger's equation with a quadratic potential for x'>~9.4 and an infinite potential for x'<~9.4.) Of course, we can't sum all the terms of the infinite sum. I've limited the sum to the 17 eigenfunctions near the n=52 eigenfunction. Thus the sum using these 17 b_n does not exactly equal the initial f(x'). The below plot displays (in black) f(x') and (in red) the sum using these 17 b_n.

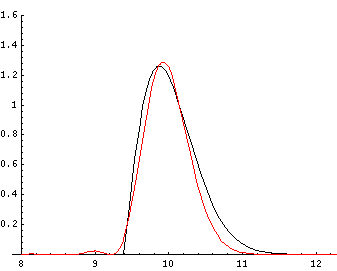
The missing terms would contribute only 5% additional probability, so it's a fair approximation. To see how this probability lump moves with time, we need only use the time dependence of the energy eigenfunctions:

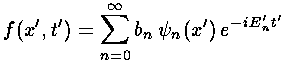
The previous page shows the results: the lump of probability moves just like a classical particle (with broadening of the lump caused by Heisenberg-required uncertainty in initial velocity).