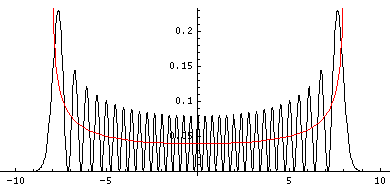
One way of making some sense out of the QM results is to ask: "What would classical mechanics tell us if the only information we had about the particle was its energy?" Looked at this way, it's not surprising the position probabilities don't change with time: we always have exactly the same information (only the given constant energy) so we must have the same probabilities. We can say that the particle must be moving around in the classically allowed region: |x|<A=(2E/k)½. All subdivisions within the classically allowed region are not equally probable, as the particle is whizzing through equilibrium, while spending more time in the parts through which its slowly moving. The time (dt) a particle spends in a little region dx depends on its speed: dt=dx/|v|. The probability (dP) of finding the particle in dx is then proportional to the time it spends there: dP=dt/T, where T is the period: the time it takes the particle to complete a cycle. In the below, the red line shows the classical probability density, and the black the exact QM result for n=32.

You can see that the classical result is essentially the average of the quantum mechanical result. Saying it differently: the main difference between results is QM has "waves". (Under many conditions the wavelength is so short, that any position probability measurement lumps together lots of waves, and hence just measures the average, i.e., the classical result.)
The wave nature of everything is the main surprising result of QM. De Broglie first argued for it seeking a unified picture of everything. So if part of everything (e.g., light) shows wave properties, all of everything must show wave properties. He said the wavelength of a particle was given by:
 =h/p
=h/p
where h is Planck's constant and p is the particles momentum. Of course, in quantum mechanics particles don't have a momentum, they have a distribution of of momentum, i.e., a superposition of simple sinusoidal waves. The peak-to-peak distance is essentially a measure of the most common momentum at that location [not a totally correct statement, but good enough for this document].
Thus where the particle is moving quickly--like near x=0-- expect short wavelengths, where the particle is moving slowly--like near ±A expect long wavelengths.
There is one other definite difference between the classical result and the quantum result. Classically you never find the particle beyond ±A. In QM there is a small chance of finding the particle in the classically disallowed region, and the chance gets ever less as you move further and further into the classically disallowed region.
Here is one last look at a wavefunction. Notice: (1) smaller amplitude where the particle is moving fast (2) shorter wavelength where the particle is moving fast (3) small and decreasing probability of finding the particle beyond the classically allowed region [which in this case ends at about |x|=8, see the red dots].
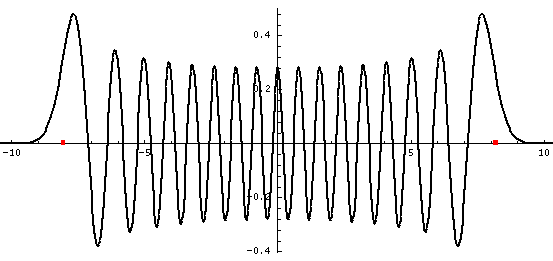
The mathematical version of the above three rules is called the WKB approximation.