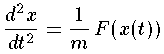
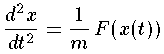
In quantum mechanics the primary aim is to solve the time independent Schrödinger's equation to find the probability amplitude (i.e., the wavefunction) as a function of position.
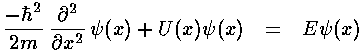
Note again the huge shift between classical mechanics and quantum mechanics: what was the dependent variable in classical mechanics (x) has become the independent variable; what was the independent variable (t) has disappeared. Later we'll see how motion is possible if time plays no role. It turns out energy (E) is more measurable than motion, hence energy has replaced time as the most important variable.
Almost any "real" problem in classical mechanics (e.g., a real cannon ball flying through the Earth's atmosphere) is so complex that it cannot be solved using paper-and-pencil methods: the differential equation must be solved "numerically" using a computer. Quantum mechanics only makes things more difficult. Only the simplest examples have "analytical" solutions (i.e., the answer can be written down using "well known" functions). The purpose of these textbook problems is to provide examples where all the dependencies are explicit so that they are available for play/understanding.
If a problem has an analytical solution, say,
=f(x)
where f(x) is some "well-known" function, consider the
consequences. Just about "every-known" function requires
that its argument be dimensionless. (I can think of only two
counterexamples.) Thus =sin(x),
or =exp(-x2) cannot be
proper answers if x has the units...you cannot take
the sine of 1 meter, nor have a power that is 1 square-meter.
Thus answers must be of the form:
=f(x/L)
where L "sets the scale" of the problem, i.e., has units that cancel those of x. Thus the first point-of-attack on any physics problem is to determine how you could form quantities like L that allow you to form dimensionless quantities like x/L.
In the classical mechanics problem, we have "givens" of
, v0, and x0.
From these one can form two scales for both time and length:
time scales:
1/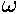 & x0/v0
and length scales:
x0 & v0/.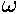
Thus the classical problem is actually a generally more difficult
"two-scale" problem that in this case has an easy solution because
one time scale enters in only in the dimensionless ratio:
x0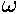/v0 = tan 
.
Thus we end up with simple one-scale dependencies like:
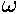t+.
Similarly there is really only one length scale in the solution:
A which is just the square root of the sum of the squares of the
above two length scales.
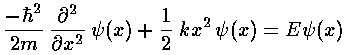
In the quantum mechanical problem we loose the "givens"
v0 and x0 (there is
no single position or velocity), and we gain a quantity
with 
. In particular, Schrödinger's
equation has constants: 2/2m=A
and ½k=B. B has the units of force/length.
A has the units of
energy·length2=force·length3.
Thus l=(A/B)1/4 has units of length
and e=B·l2=(AB)½
has the units of energy.
It is worthwhile to calculate the numerical value of these scales
and see how easy it would be to observe the quantum harmonic oscillator.
| particle | frequency | length scale | energy scale |
|---|---|---|---|
| H2 vibration | 1.3×1014 Hz | .01 nm | .23 eV |
| O2 vibration | 5×1013 Hz | .005 nm | .10 eV |
| CCl4 symmetric stretch | 1.4×1013 Hz | .002 nm | .03 eV |
| simple nuclear model | 2×1020 Hz | 7 fm | .4 MeV |
| simple meson (bb) model | 1×1023 Hz | .2 fm | .2 GeV |
(Note f=femto=10-15.) Molecules typically vibrate a small fraction of their interatomic separation. Nuclear vibrations are often modeled with a liquid drop model---a lot of the nuclear mass is not moving, instead we have something more like a surface wave. Room temperature thermal energy (~ .03 eV) is comparable to (often a bit smaller than) molecular vibration energy.