We have accelerated motion in the z direction:
z(t) = z0 + vz0t - ½gt2:
vz(t) = vz0 - gt
where the initial height (z0) and the initial z velocity (vz0) are the boundary conditions needed to solve classical equation of motion:
z'' = -g
and uniform (constant velocity) motion in the y direction:
y(t) = y0 + vy0t
vy(t) = vy0
where the initial down-range position (y0) and the initial y velocity (vy0) are the boundary conditions needed to solve classical equation of motion:
y'' = 0
Motion in the y direction is "free" (i.e., free from forces) and unbounded (i.e., if vy0 is not zero, over all time, the particle reaches every possible y position). Motion in the z direction is bounded between the perfectly elastic ground (at z=0) and some maximum height (zmax) that depends on the initial "z" energy Ez. (Note that energy is certainly not a vector, rather the totally separate differential equations for z and y have separate constants-of-motion which exactly correspond to the one-dimensional concepts of energy. Thus:
Ez = ½m vz2 + mgz
and
Ey = ½m vy2
are separately conserved quantities that sum to form the total energy E.)
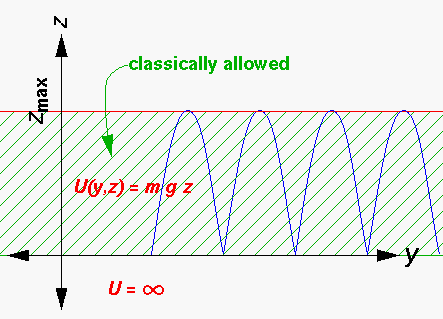
Classically the trajectory is a series of parabolic bounces (in blue):

Note that the full separation of y motion from z motion means that positions that are energetically allowed like:
E/mg > z > zmax
cannot actually occur. A slight coupling of y and z motion (e.g., that would occur if the z=0 ground plane were slightly bumpy) would expand the allowed region to include the above region.