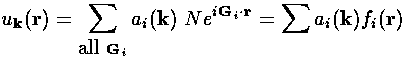
As stated before, a periodic function like uk can be expanded as a sum of reciprocal lattice vector waves like:
N exp(iG·r) = fi
where G is a reciprocal lattice vector and N=1/(a2 sin 60°)½ is a normalizing constant that forces the integral over a real lattice cell to be 1. (a2 sin 60° is the area of a lattice cell; the square-magnitude of the exponential part is 1.) The result is a Fourier series:
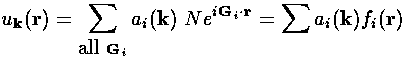
Now uk must satisfy the Schrödinger's equation:
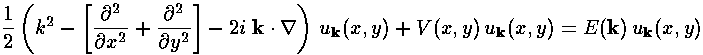
which we write simply as:
H uk = E(k) uk
We now do the usual Fourier trick to isolate a particular expansion coefficient ai. We multiply both sides of the Schrödinger's equation by fi* and integrate over a lattice cell...orthonormality of the fi reduces the sum on the rhs to a single term; on the lhs we have a sum over all possible reciprocal lattice vectors labeled by j.
 < i | H | j > aj =
E ai or
< i | H | j > aj =
E ai or
[H]·[a] = E [a]
where:
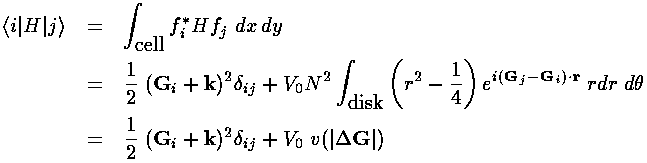
Notice that we diagonalize the kinetic energy part of the Hamiltonian at the expense of spreading V--which was diagonal in the grid approximation--all over the matrix. Mathematica (or knowing a bit about special functions) allows us to express the V integral in terms of Bessel functions: J.
So far all is exact: instead of solving Schrödinger's differential equation we are now requested to solve an infinite-sized matrix eigenproblem. Our approximation consists of truncating the infinite matrix, thus including only a finite number of reciprocal lattice vectors (a.k.a., Fourier components). We justify this by noting that in the limit of "small" V0, the solutions are single waves and that the V matrix elements grow small for larger G differences...we say V causes only a small coupling of distant G. On the other hand, as V0 grows large, large G will be required to localize the ground state to a small region in space. Usually the only way to see if the truncation is a good approximation is to expand the number of included Fourier components and check to see that little is affected.
Below is a plot of the V matrix elements as a function of the magnitude of difference in G vector. The dots show the G vector differences in the actual reciprocal lattice. Notice that the diagonal V matrix elements (which are much larger: about -0.1) are not plotted since they produce only a uniform energy shift
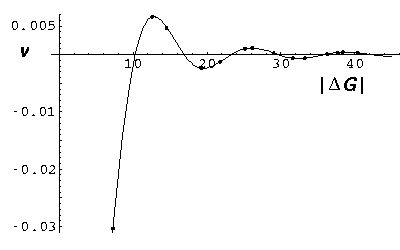
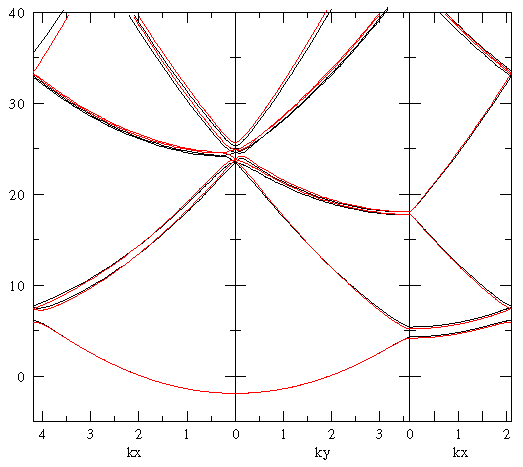
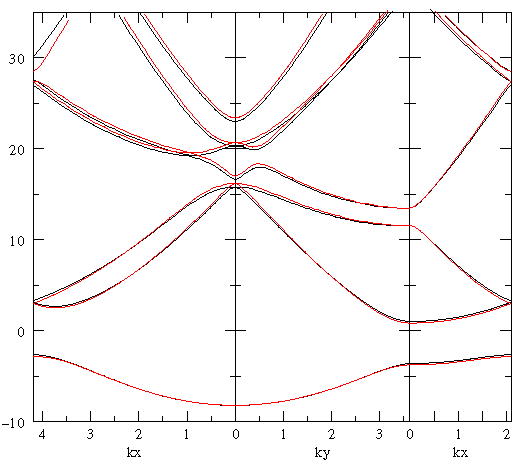
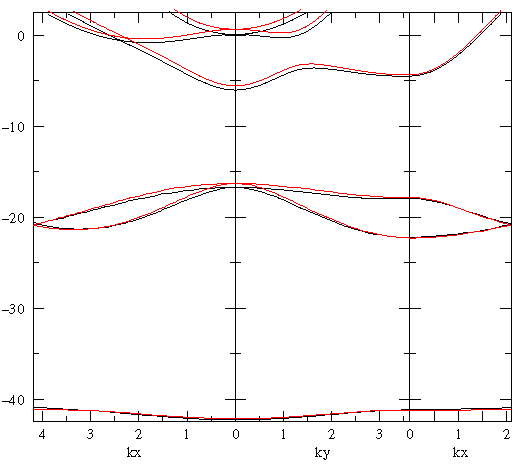
We now compare the results of band structure calculations using the 37 reciprocal lattice vectors within 3× the nearest neighbor distance (i.e., a 37×37 matrix eigenproblem); to the h=1/16 grid (which produces a 256×256 matrix eigenproblem). In the below plots the red lines are the new plane-wave approximation method and the black lines are the grid approximation. They agree closely, but the 37×37 matrix eigenproblem is solved about ten times faster.