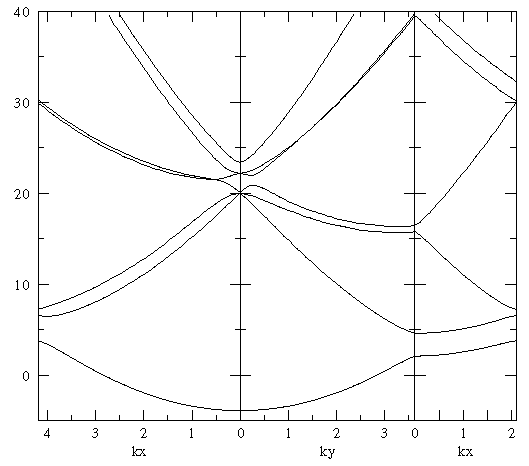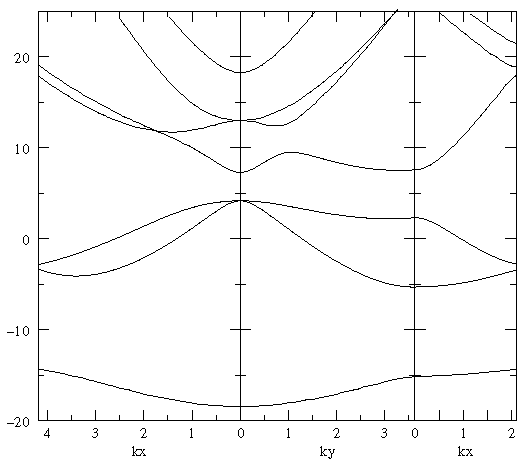
V = V0 (r2-¼)
for various values of V0 using numerical calculation of the eigenvalues of the 64×64 matrix that comes from h=1/8. (Occasionally we will check results using the 256×256 matrix that comes from h=1/16, but these results take much longer to compute.) For comparison we note that this 2D potential, if continued to infinity rather than fit into a lattice, would have its excited state at E=0 for V0=128.
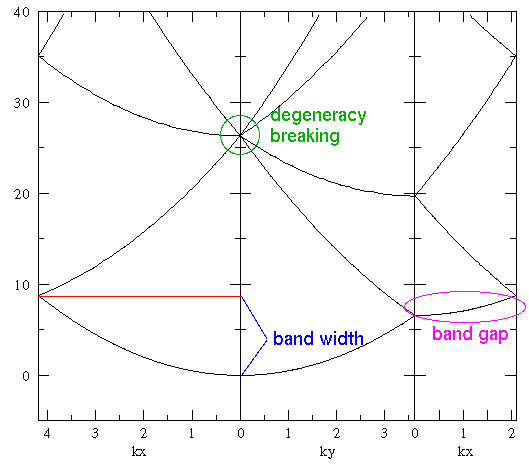
Many interesting features can be found in the below plots. For a first viewing I draw your attention to three areas on a plot (the base plot is the exact free solution):

The nearest-neighbor bands are six fold degenerate at k=0. For k along our usual tour the bands have various degeneracies. How are these degeneracies broken? Note that for the simple harmonic oscillator the first excited state (1p) is doubly degenerate, and the second excited state is triplely degenerate (2s+1d). With l-tilting, we'd expect the order of states to be: 1s, 1p[2], 2s, 2d[2].
For the free lattice, the first and second states are degenerate along the zone boundary. Watch for this degeneracy to be broken.
For the free lattice the curvature of the ground-state band is that of a free particle. Look for this curvature to decrease, i.e., for the ground state band width to decrease.
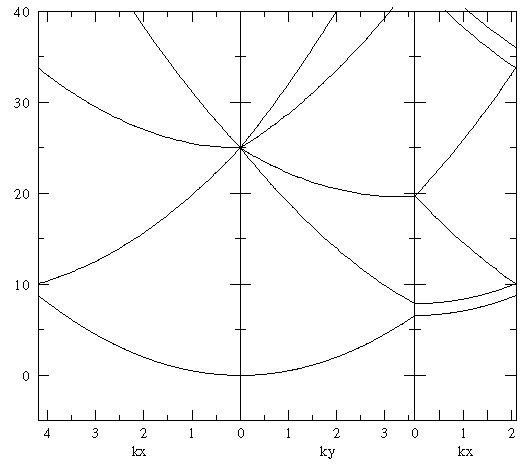
Note that this numerically calculated set shows the computational artifact of a band gap. If h is reduced we'd reproduce the above exactly calculated band structure.
Note that this numerically calculated set shows a band gap. Is it an artifact or real? Computing with h=1/16 (rhs graph) shows the gap much the same (rather than reduced by 3/4 as it would be in the free solution). Apparently this gap is real.