H-atom p.8
Spin and Spin-Statistics
The Spin-Statistics Theorem concludes
wavefunctions must have definite symmetry (even or odd)
when the coordinates of identical particles are exchanged.
So, for example, all multi-electron wavefunctions
must have the property that if the coordinates of any two electrons
are exchanged, the resulting function is (-1)× the original
function. Electron wavefunctions must be antisymmetric (i.e.,
"odd under exchange"). On the other hand, all multi-pion wavefunctions
must have the property that if the coordinates of any two pions
are exchanged, the resulting function is the same as the original function
(i.e., "even under exchange"). A particle is called a fermion
if its wavefunctions must be odd under exchange. A particle is called
a boson if its wavefunctions must be even under exchange.
The Spin-Statistics Theorem concludes that
the determining feature as to whether a particle is a boson or
a fermion is the spin of the particle. Just as the
planet Earth is both spinning on its axis and orbiting the Sun, so
electrons are spinning on their axis while orbiting the nucleus
in an H-atom.
With enough energy the Earth could be made to spin slower or faster
[in fact the Earth's spin is slowing over aeons] or orbit
with more or less angular momentum. While the electron's
orbital angular momentum can change (i.e., various integer
values of l are allowed), it always is seen with
exactly the same spin-rate. The only possible change that
can be made to an electron's spin is to change the direction
of the spin orientation: "up" (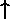 ) or "down"
(
) or "down"
(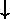 ). Thus
the spin angular momentum of a fundamental particle is an unchanging
characteristic of the particle. The rules
of quantum mechanics guarantee that spin angular momentum
of a particle must be [s(s+1)]½
). Thus
the spin angular momentum of a fundamental particle is an unchanging
characteristic of the particle. The rules
of quantum mechanics guarantee that spin angular momentum
of a particle must be [s(s+1)]½
 , where s (hereafter called the "spin
of the particle") is either a whole number (0, 1, 2,...) (
so called "integer spin") or half of a odd whole number (1/2, 3/2, 5/2, ...)
(so called "half integer spin").
Integer spin particles are always bosons; half integer spin particles
are always fermions.
, where s (hereafter called the "spin
of the particle") is either a whole number (0, 1, 2,...) (
so called "integer spin") or half of a odd whole number (1/2, 3/2, 5/2, ...)
(so called "half integer spin").
Integer spin particles are always bosons; half integer spin particles
are always fermions.
| Fermions
|
|---|
Particle
Name | Spin
|
|---|
| quarks | 1/2
|
| electron | 1/2
|
| proton | 1/2
|
| neutron | 1/2
|
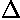 | 3/2
|
| He3 nucleus | 1/2
|
| O17 nucleus | 5/2
|
| Bosons
|
|---|
| photon | 1
|
| gluon | 1
|
| graviton | 2
|
| pion | 0
|
| H2 nucleus | 1
|
| He4 nucleus | 0
|
| B10 nucleus | 3
|
On the previous page we made both symmetric and antisymmetric
two electron wavefunctions. However our wavefunctions just included
the spatial part of the wavefunctions. The spin part of a two
electron wavefunction can be:
symmetric: 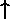
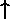 ,
(
,
(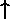
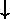 +
+ 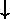
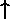 ),
),
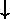
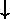
antisymmetric: (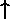
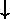 -
- 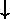
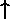 ),
),
(Notation: the first arrow in a pair refers to electron 1 spin and the second arrow
to electron 2 spin.)
Thus in order to made an overall antisymmetric wavefunction we need to pair
one of the three symmetric spin wavefunctions with an antisymmetric spatial
wavefunction (hence the name: triplet), or pair the single antisymmetric spin
wavefunction with a symmetric spatial wavefunction (hence name: singlet)
Thus the ground state of Helium can be written:
1s(r1)1s(r2)
(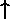
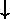 -
- 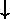
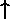 ),
),
One of the excited states considered on the previous page might be written:
(1s(r1)2p(r2) -
2p(r1)1s(r2))
Note that is impossible to create a totally antisymmetric function
of three electron spins. Thus the Pauli Exclusion Principle
that at most two electrons can be in the same spatial wavefunction.
(If two electrons share a spatial wavefunction, they must be in the
spin "paired", i.e., singlet, state.)
Thus two electrons can fit in the 1s state, six
electrons can fit in the 3 (m=-1,0,1) 2p states, and
ten electrons can fit in the 5 3d states.
One is tempted to connect the characteristic of 2 electrons "filling up"
an orbital, with the naive idea that "you can't put two things in the
same place". However, note that a Uranium atom, with its 92 electrons
"filling" the orbitals with n<5, will happily latch on to the negatively
charged muon (µ-: a spin 1/2 particle similar to the electron
but about 200 times more massive) which can occupy its own 1s orbital.
However if three muons are attached to Uranium, the third must go in the
2s state. Any number of negatively charged pions (a psin 0 particle
a bit more massive than the muon) can enter the 1s state, even
though there are two muons and two electrons in the 1s state.
That is to say that the Spin-Statistics Theorem says nothing about the
exchange properties of different types of particles, only identical particles.
Next
 ) or "down"
(
) or "down"
( ). Thus
the spin angular momentum of a fundamental particle is an unchanging
characteristic of the particle. The rules
of quantum mechanics guarantee that spin angular momentum
of a particle must be [s(s+1)]½
). Thus
the spin angular momentum of a fundamental particle is an unchanging
characteristic of the particle. The rules
of quantum mechanics guarantee that spin angular momentum
of a particle must be [s(s+1)]½
 , where s (hereafter called the "spin
of the particle") is either a whole number (0, 1, 2,...) (
so called "integer spin") or half of a odd whole number (1/2, 3/2, 5/2, ...)
(so called "half integer spin").
Integer spin particles are always bosons; half integer spin particles
are always fermions.
, where s (hereafter called the "spin
of the particle") is either a whole number (0, 1, 2,...) (
so called "integer spin") or half of a odd whole number (1/2, 3/2, 5/2, ...)
(so called "half integer spin").
Integer spin particles are always bosons; half integer spin particles
are always fermions.