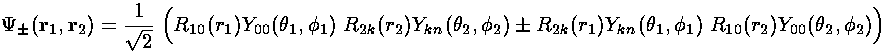
Consider the following functions of the vector coordinates of three particles: a, b, and c.
f(a,b,c)=|c| |a-b|
g(a,b,c)=|c| (|a|-|b|)
h(a,b,c)=|c| |a| |b|
f is symmetric under exchange of a and b, because:
f(a,b,c)=f(b,a,c)
g is antisymmetric under exchange of a and b, because:
g(a,b,c)=-g(b,a,c)
h is fully symmetric under exchange, because:
h(a,b,c)=h(b,c,a)= h(c,a,b)=h(a,c,b)= etc
f is neither symmetric nor antisymmetric under exchange of a and c, because:
f(a,b,c)=|c| |a-b|
and
f(c,b,a)=|a| |c-b|
have no particular relationship.
Thus if we want to have one particle in the 1s and the other in the 2p state there are two possible ways:
symmetric: 1s(r1)2p(r2)+ 2p(r1)1s(r2)
antisymmetric: 1s(r1)2p(r2)- 2p(r1)1s(r2)
The sort of wavefunction we were considering:
1s(r1)2p(r2)
has no particular symmetry and is ruled out.
Note that if we wanted both particles in the 1s groundstate our only choice would be to make a symmetric function:
1s(r1)1s(r2)
Let us then construct symmetric and antisymmetric versions of the wavefunction we were considering on the previous page and calculate the energy correction for those states.
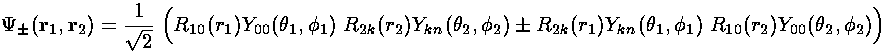
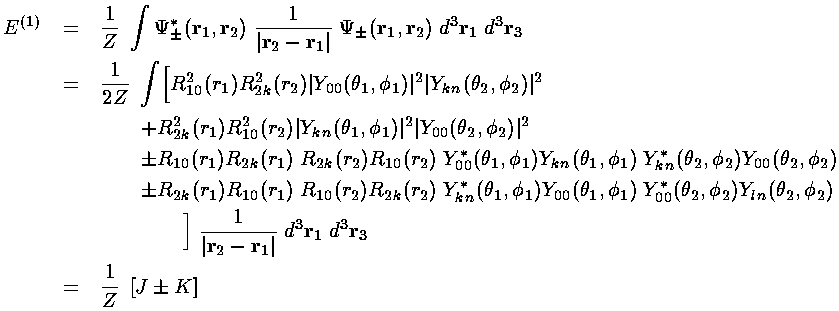
Note if we perform a change of variables in the second integral:
renaming r1 
r2
and r2 r1,
|r2-r1| is invariant and the second
integral is seen to be exactly the same as the first. We call this
common integral the direct interaction integral and name
it J. Note that J is the integral calculated
on the previous page. The same game on the fourth integral shows
it to be the same as the third. We call this
common integral the exchange interaction integral and name
it K.
We proceed to evaluate K much as we did J: by plugging in our expansion for 1/|r2-r1| in terms of the Ylm:
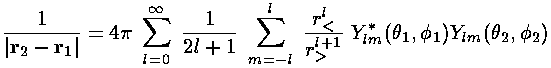
Thus the integral K becomes a sum of integrals with a typical term like this:
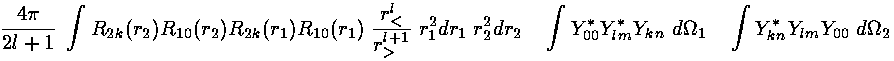
The Y00 factors are in fact constant and can be pulled
outside the integrals (where they can cancel the overall 4
factor); the resulting 2-Ylm integrals
are either 0 or 1 by the usual orthonormality of the Ylm.
Thus the sum of terms reduces to one term; the lm in the sum must match
the kn in the wavefunction.
We are left doing the radial integral using Mathematica:
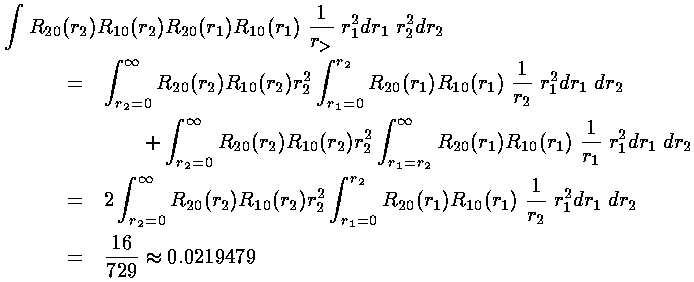
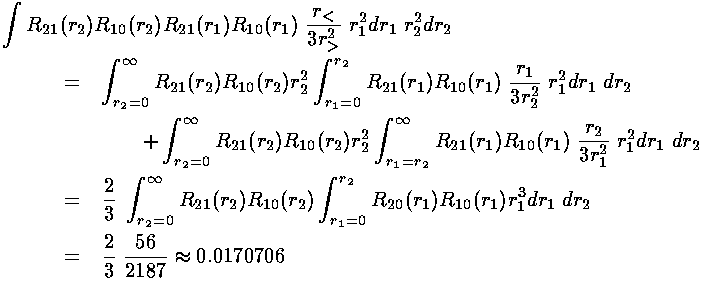
The energy of the 1s2s symmetric state (called parahelium or singlet) is approximately:
-½(1+¼)+½(0.209877+0.0219479)= -0.509
The energy of the 1s2s antisymmetric state (called orthohelium or triplet) is approximately:
-½(1+¼)+½(0.209877-0.0219479)= -0.531
The energy of the 1s2p symmetric state is approximately:
-½(1+¼)+½(0.242798+0.0170706)= -0.495
The energy of the 1s2p antisymmetric state is approximately:
-½(1+¼)+½(0.242798-0.0170706)= -0.512
i.e., the orthohelium (antisymmetric, triplet) 2p state lies .019×(Z227.2 eV)=2 eV above the orthohelium 2s state; the parahelium (symmetric, singlet) 2p state lies .014×(Z227.2 eV)=1.5 eV above the parahelium helium 2s state. Again, the splittings are about a factor of two too large, but the relative placement of states agrees with experiment.
The main point here is that the antisymmetric states [i.e., the states that will turn out to have the largest net electron spin] lie below the equivalent symmetric states. The reason for this is the antisymmetric wavefunction must be zero if evaluated where r1=r2. Thus there is no probability that the electrons are on top of each other, and via wavefunction continuity a generally small probability that the electrons are near each other. The repulsive electron-electron interaction is minimized by having the electrons relatively far apart.