By Seville Chapman
The text has not been altered or edited to ‘bring it up to date.’ It is a product of its times, written just after World War II. Physicists and physics students are referred to as ‘he’ not out of sexist motivation, but is a reflection of the plain fact that at that period of history almost all physicists and physics majors were male.
The two-term freshman physics sequence at universities was a non-calculus course taken by pre-med, pre-dent and pre-pharmacy students. Physics majors usually (but not always) took a parallel calculus-oriented freshman course. At most schools the science requirement for all students was ‘a year of laboratory science’ chosen from one of the natural sciences: chemistry, physics, biology, geology, or astronomy. These non-science students took the same introductory course the science majors took, there being no ‘special’ courses for non-scientists.
Despite the age of this document, its recommendations for effective study of physics remain appropriate even today, especially for those students who really want to learn the subject. The problem examples, using English units, have been left unchanged. The references to tuition costs and textbook prices are a reminder of how much inflation has occured since then.
Chapter 10, and part of chapter 9 are omitted from this HTML version. Only excerpts are included from chapters 1 and 2.
Footnotes are linked. To return from a footnote to where you left off in the text, click on the chevron symbol: §
The editor has added a few explanatory and supplementary footnotes, in italics, identified with the initials DES.
Donald E. Simanek
Lock Haven University
January, 1996.
A proper mental attitude toward the material to be studied is the primary requirement. You must earnestly want to learn. Unless you are finally convinced that you want to do a good job in your physics work, this manual will do little good. Unfortunately, resolutions alone do not help. Learning physics takes work. This guide points out how you may work effectively but it cannot tell you of short cuts because there are none. Every suggestion included here has been of use to somebody—a fact verified by student comment on an earlier version of this book. A few of the ideas are mutually inconsistent since not all students study most effectively in the same way. Try out the various schemes and then develop a system or study that is suited to you.
A student who read a rough draft of this material said that anyone who followed all the suggestions in it would be sure to get an A in physics but would fail every other course from having spent all of his time on physics! Certainly it is up to you to decide what part of your time you should devote to physics. It is a fact that you can learn to use that time efficiently.
There are several full-size books on how to study, but most of them tend to be rather general. [1] In this guide an attempt has been made to give numerous specific examples, and a summary of the main ideas has also been included...
SEVILLE CHAPMAN
Stanford University, California
August 1946
Experience has shown that people whose training has developed their ability to think clearly and whose studies in several different fields, including physical or biological sciences, humanities, and social sciences, have also given them a liberal, tolerant, and understanding attitude toward life, are more able to make a significant contribution to human welfare than those without that training. If you prefer less sophisticated language, you may say that people with the qualifications just mentioned make the best citizens. Furthermore, because of the breadth of their background, such people are able to lead full and rich lives and to enjoy many kinds of things. ln a materialistic sense, such people are likely to be capable and hence they deserve to hold responsible (and well-paid) positions.
The professions require not only specific technical training but also tolerance and the ability to think clearly. A college or university is an ideal place to obtain such training...
Good character is made up of many worthy qualities, including self-discipline, reliability, honesty, tolerance, and the ability to get along with other people. It should be a prime objective of the college student to develop these characteristics. There are many opportunities to do so: for example, studying even when there is no immediate prospect of an exam, doing a clean, thorough job in the lab without, for instance, reading the scale in such a way as to favor a result in agreement with the ‘true’ or handbook value; and learning to get along with fellow students in a pleasant, friendly, cooperative way.
As a check on his aptitude, a serious-minded student will take courses in several different departments to find out in what field he can do the best work. This is quite distinct from finding out where he can get the best grades...
...All professional students, however, should be impressed with the fact that their technical knowledge rapidly goes out of date, not because it is wrong but because new and better methods and techniques are developed... Over a working life of perhaps for years, you must learn a great deal more after you leave college than before. Therefore, as an undergraduate, be sure to learn how to learn by yourself.
...As it is evident that anyone can find all the facts of physics merely by going to the public library, a [student] is hardly equipped if he knows only facts. If he knows principles he is somewhat better off but not likely to be worth much to an employer, who can learn the principles himself by a little study. The methods and techniques are about equally important and can be acquired only by practice on typical problems...
Consequently, it is clear that the real purpose of taking first-year physics is not to ‘get’ facts and principles, although these are essential, but to train one’s thinking through practice on simple problems so that later on more difficult problems and situations can be approached effectively. For this reason discussion questions, homework problems, and practice on similar problems are very important aspects of first-year physics for the professional man. The student who goes beyond first-year physics is likely to stay on the right track if he constantly asks himself the following questions about every new fact or theory:
Granting, then, that there are reasons for studying physics, we may return to our problem of how to study it effectively. In physics, perhaps more than in any other subject, it is necessary to develop an ability to analyze problems, to reason logically, and to discriminate between important and irrelevant material. Consequently, efforts to memorize physics are practically worthless. For most students physics involves many new concepts. To master the material takes work, and that takes time. Although you must decide how much time you can devote to physics, we hope you will learn enough from this discussion to develop a good system of studying. You must realize that a university cannot educate you. You must do that for yourself, although a college or university is the place where it is likely that you can study most efficiently.
Probably you have heard many of these ideas before. Some of them apply to any course, some are specifically related to physics. Although not all the ideas will appeal to a given individual, any suggestions appearing here have been of value to some student. Try them out. They may help you.
Get interested in the subject by learning something about it, tying it in with other courses, talking it over with fellow students. Be assured that if the course is required as part of a curriculum of professional training, the course is necessary. Try to discover why.
Go to class; be alert. Make a serious effort to stay right with the lecture Adopt a cooperative and receptive mental attitude rather than a belligerent one. Perhaps you will develop more enthusiasm for the course if you sit in one of the front rows, where you will be forced to pay attention.
Find yourself a quiet place to study, with plenty of light and desk space that is free from distractions, including radios and pictures of girl friends or boy friends. (The desk is for work; put the pictures on the bureau.) Study conscientiously, keep at it; sit with your back to the door and reject interruptions. The time you save will enable you to enjoy occasional bull sessions without worrying because you aren’t studying.
Budget your time. Make out a study schedule and stick to it for at least two weeks. Get adequate sleep, regular moderate exercise, and some recreation, but leave two full honest hours weekly per unit for study. [2]
There are 168 hours a week. Of these 168 hours you will be asleep for about 60, dressing and eating for about 20. If you take Saturday afternoon off for a hike, consider Sunday morning and afternoon as time off from studying, and have two four-hour dates a week, you have about 68 hours a week for work. If you are in class and laboratory for 20 hours, you still have 48 hours for study. It seems like a tremendous amount of time, doesn’t it?—especially considering that you’ve taken off half of Saturday and most of Sunday. Just where does all the time go? A great deal of it is lost in ten-and twenty-minute idle discussions, time wasted during the twenty minutes while you wait before a class after you’ve needlessly spent another twenty minutes walking to the post office and back for a stamp you could have picked up just as easily on your way back from lunch, and so on. It is up to you whether you want to make good use of these numerous ten; twenty, or thirty-minute intervals. I’m not urging that you never take a minute off to enjoy life, but there is certainly little danger that you will use your time too efficiently.
You learn more physics by studying it for an hour a day than by studying it for ten hours on a week end, and it takes less time. Furthermore, you will get more from the middle-of-the-week classes Don’t get behind. Keep up with your work. It’s much easier to learn your lessons from day to day than it is to half-learn them all at once on the day before the exam. If the prospect of an assignment is forbidding, begin on it; you may get more done than you expected.
Plan to study physics as soon after class as possible, while you still remember things that probably will be forgotten twenty-four hours later. You may find it a good idea to study physics when your mind is fresh, before you work on subjects requiring less concentration. During a study session of several consecutive hours, an occasional relaxation period of five minutes often is a help. Sometimes it is better to study one subject for an hour and then shift to another subject for an hour, rather than to study one course continuously. Sometimes it is not better. Experiment to find out which method suits you.
When you study, really study. Much of your time may be lost in slipshod thinking, daydreaming, following blind alleys of thought, and just plain loafing. Probably you have experienced times when your process of learning was very easy and rapid. Try to figure out how this happened and then try to duplicate the occurrence. (Sometimes the prospect of an examination provides a good incentive; can you provide yourself with an artificial incentive?) While you are studying, keep personal worries off your mind. If you have a personal problem, get some good advice, think it over, then make your decision and stick to it.
You understand a lecture better if you have some notion ahead of time as to its subject matter. For this reason, spending the five or ten minutes between classes reading the main paragraph headings gives you a better return for the time spent in the lecture than if you spend the time before class reading the daily paper. (By all means, read the newspaper later.) Experiment to find out what part of your study time for a given assignment should be spent before lecture and what part after lecture, in order to give you the best return. Probably you will spend from ten to forty percent of your time studying before lecture.
Perspective is one of the chief aims of education. To see the parts in relation to the whole is much more important than to know all the details. [3] Perspective provides a scaffolding into which the details may be fitted readily. When you study an assignment, first go over it rapidly, taking in only the high spots, to find out what it is about. Then go over it more carefully. Study to understand the material, not just to read an assignment. Go slowly Physics can’t be read like a novel or even like a history lesson. (A physics assignment is often only a half-dozen pages rather than a half-dozen chapters.) Try to think of applications of the material as you read it and of problems to which the formulas apply. Try to correlate the material with your previous knowledge and with other courses. Material in the text is not necessarily 100 percent correct. Textbook authors are human and sometimes are misinformed, just as other people are. All books have some typographical errors, although usually not very many. Be critical. Do not believe what you read unless it makes sense to you. [4]
When you finish a paragraph, think out its main idea. Say it out loud or write it down. When you finish the page, ask yourself what was on the page. It may have seemed simple when the author wrote it, but can you put it in your own words? You may have to do so in an exam.
When you finish the assignment, plan what question you would ask if you were making up an examination. Close the book and deliver yourself a three-minute formal lecture on the lesson or, if you feel silly talking to yourself, write out a fifteen-minute essay on the subject. Probably you will discover that you didn’t know the material as well as you thought you did—better to find it out while studying than during an exam. The importance of frequent self-recitation cannot be overemphasized. Review the day’s work in the evening, the week’s work on Friday, and the whole course once a month.
Psychologists say that if you overlearn material (i.e., study it somewhat longer than is necessary just to understand it), you will remember it later with comparative ease. Furthermore, overlearning and review show you where you are weak and give you a chance to clear up the weak points.
Physics can be learned by seeing, hearing, reading, writing, and talking. Do not overlook the chance of talking things over with your friends. An excellent study procedure is for two students to study a week’s material together and then give each other an oral exam on it. (Let A ask B a question. If B answers, it is a point for B; if B cannot answer but A can, then it is a point for A. The one with the most points can call the tune but perhaps the loser will want to study a little more.) Trying to explain something to a critical friend will show if you really know it. Don’t delude yourself by saying, “I know it but I can’t explain it,” for if you do understand it, you can explain it. As a matter of fact, a good test of your understanding is furnished by the ease with which you can explain something. When you understand it well enough, you can explain it easily.
As you are outlining the course, revising your lecture-notes, reading the text, or doing problems, occasionally you will come upon things you simply cannot understand. Don’t say: “I can’t get it at all.” Rather, try to analyze your difficulty so that you can state specifically what you don’t understand. Make a list of these difficult topics and ask the instructor about them at the next class. Don’t hesitate to ask, either. Probably there are others who will be glad to know the answers too. Contrary to popular student impression, the instructor probably will be pleased that you ask about the course.
If you are having real difficulty with a course, spend an hour writing an essay on what you think the course is about, what its significance is, how it should be studied, why you are taking the course (or if it is a required course, why you think it is required), why you think you are having difficulty, etc. Then show your instructor the essay but ask him to count ten before he says anything. Very likely your essay will be of value to him in diagnosing your difficulty and prescribing a remedy. Writing the essay certainly will help you to profit from your instructor’s diagnosis and remarks.
If the course seems to be too deep for you, try going to the main library or to the physics library, where there are some books simpler and easier to understand than your text. The instructor will be able to suggest several books of this type, But don’t neglect your own book. It has an index and probably several appendices. They may help. Use your own book; don’t just read it. Underline important points, put your own comments in the margin, etc. (If it costs $500 to $1000 for you to take a physics course, it is hardly worth while to worry about the resale value of a $5 text.)
Sometimes a student can learn more in an hour from a good tutor than he could in a whole evening by himself. Your instructor will know of some good tutors. Or the material may not be so difficult as you think. Don’t expect too much. A thing may have a terrifying name (such as a prolate spheroid) but may actually represent something simple (a football). The sentence following an obscure one may clear up the trouble.
If your physics suffers because it takes you too long to read your history lesson, speak to your adviser, who will be able to suggest corrective procedures. Most people can greatly increase their reading speed and degree of understanding if they go about it in the proper way. [5]
Pay special attention to definitions. Often a common word has a special technical meaning; be sure you understand it. Although in common parlance such terms as force, energy, work, and power often are used synonymously, all of them have distinct, different meanings in physics. Learn these meanings. For nontechnical words about which you are in doubt, use a dictionary. All students should own and use a good dictionary. Definitions are important not because they may be asked for in an examination but because a clear and concise formulation of the meaning of a defined quantity is essential to an understanding of it. Incidentally, do not merely mimic the words in the text but study for a grasp of the subject so that you can give the definition in your own words too.
Take an active part in recitation work. Ask questions. Try to anticipate what will come next. Such an alert mental attitude will help to make the material sink in.
In technical courses, undoubtedly you will have numerical problems to work from time to time. In addition to quantitative problems, however, discussion questions are very useful learning aids. If your text has questions of this type, be sure to go over them. If, after thinking hard, you cannot get the answers, ask your instructor for some hints. If your book does not have this type of question, you should either get a book that does or else ask enough questions in your recitation section so that you get the benefit of this kind of mental exercise.
Taking good notes in a physics lecture is quite different from taking good notes in, say, a history class. One of the main differences is that most history lectures are largely the presentation of factual historical material, whereas most physics lectures are primarily the explanation of a comparatively small number of principles. These usually are illustrated by examples and by demonstrations. Outline form is good in history because it may be impossible to write down all the facts as rapidly as they are given to you, but if you use outline form in physics, at the end of a lecture you have only a portion of a page of notes, and probably they are not very illuminating. Outline form is unsuited to physics because in an outline you will not get down enough of the explanation to help you much afterwards. For explanation put down complete sentences (subject, predicate, object, etc.) but abbreviate long words. If you expect to be able to ‘decode’ your notes later, do not omit important words whether they be verbs or prepositions, In physics it makes a lot of difference whether a force is exerted by one object on another, or vice versa. To illustrate, on the subject of the ballistic pendulum the professor explains: “The kinetic energy of the bob at the bottom of its swing is equal to its potential energy at the top of its swing. Therefore from the height to which the bob swings, one can calculate what its velocity was at the bottom of the swing, in the following way....” The good note-taker writes: “KE of bob at bottom of swing = PE at top. :. from height bob swings can calc vel at bottom thus...” [6]
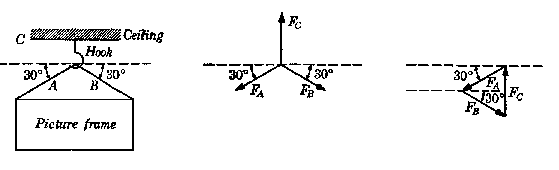
Diagrams or formulas are put on the board. Actually they are the least important things to put in your notes, since they can be found afterwards in the text. The main thing to record is the explanation that accompanies them. (You will understand the explanations better if you spend some of your time studying before class.) If a diagram is labeled on the board, be sure to put down all of the labels. Three arrows coming from a point may mean nothing in your notes but, if they are accompanied by several sentences of explanation and by appropriate labels on the diagram, they may show the complete story of the forces acting on some point of a complicated structure such as a cantilever bridge, or they may show something simpler, thus:
The professor says (and draws the diagrams):
“A picture frame hangs from a hook in the ceiling C by two strings A and B, each making an angle of 30° with the horizontal. There are three forces acting on the hook, the upward pull FC exerted by the ceiling, and the two downward forces FA and FB due to tensions in the strings A and B. Since the hook is at rest, it must be in equilibrium, and we may apply the force-polygon method to determine the relationships among the various forces...”

You copy the diagrams and write:
“Picture hangs from hook. Forces acting on hook are upward pull FC exerted by ceiling and downward pulls FA and FB exerted by strings. At rest :. equilibrium :. polygon method....”
Probably the professor will show how FA, FB and FC are related and then go on to discuss the forces acting on the ceiling or the forces acting on the picture frame, none of which has been mentioned yet.
One of the most deflating experiences a professor can have is to examine the notes taken by students in his classes. In the example above, the professor probably puts nothing on the board except the diagrams (writing many sentences on a blackboard makes a dull lecture) and some students’ notes consist of nothing but the diagrams. The important ideas, however, are in the application of the principles to the specific problem represented by the diagrams. In other words, the explanation that accompanies the diagram is the most important part of the discussion and the student—if he takes any notes at all—should put the explanation in his notes. If the instructor goes too fast, ask him a question to slow him down; for example, “Would you state that conclusion again, please?”
For most students, two to four pages of notes is a reasonable amount for one physics lecture, Do not ignore the demonstrations. Draw a diagram of the experimental setup and tell what principles are illustrated. If you don’t know what the demonstration is supposed to demonstrate, ask the instructor.
If the lecturer follows a text rather closely, study the book before class, take it to class, keep it open, and make notes in the margin or on a separate sheet of paper.
Some students find it better to take no notes at all during lecture (or to take very sketchy ones) and to spend the full time concentrating on what is being said without being distracted by frantically trying to write everything down. Immediately after lecture, they write out a complete set of notes (with detailed explanations), using the text (and their sketchy notes, if any) to aid them in remembering what was discussed.
Sometimes students pair off, one of them concentrating on getting good notes (making a carbon copy) and the other concentrating on digesting the explanation. After class they discuss the lesson together. While this procedure has something to recommend it (especially in advanced courses), it puts too much emphasis on the importance of notes.
Psychologists say that the physical operation of writing a set of notes contributes something to the learning process, in addition to the fact that the material being written almost of necessity has to have made some mental impression. Therefore you must have at least one set of notes in your own handwriting. This set ought to serve the double purpose of being a learning aid physically, as well as helping in review. Consequently, whether or not you take notes in lecture, when the lecture is over your note work has only begun. While the material is still fresh in your mind (preferably within a few hours after lecture), go over your notes and smooth them out. Add to the explanations. Compare the lecture with the text and fill in the parts you missed. If the material still seems obscure, consult another text in the library. Pick out the important statements in the notes and the important formulas; then underline them with red pencil to facilitate your review for exams. It is likely that in a whole term’s work there will be fewer than twenty important formulas you must know. But remember it is the method of applying them that really counts.
In working problems, it is very important to do the work in an orderly fashion:
There is a definite (although not complete) correlation between orderly work and orderly thinking. Do your problems as neatly as you can the first time, preferably in ink. Being neat has a tendency to stimulate clear thinking. The same idea applies to lecture notes.
After reaching the answer to a problem, you should go over the problem, work it backward (i.e., with the answer as a known quantity and one of the given quantities as the unknown), make modifications in the problem, and do it again. For instance, the problem may be: “A stone falls from rest from a tower 144 feet high; neglecting air friction, calculate the time for the stone to reach the bottom.” The answer is 3 seconds. Working the problem backward involves solving this problem: “Calculate the height to which a baseball goes if it takes three seconds to drop to the ground from the highest point in its flight.” A variation of the problem is: “A first-aid kit dropped to a stranded mountaineer from a helicopter 144 feet above the ground is falling with what speed just before it strikes the earth?”
Under no circumstances can you regard your problem study as being sufficient if you merely get the right answer and then stop. The instructors and the readers [11] already know the right answer anyway. Doing the problem is worthwhile only insofar as it gives you training in thinking. You get a poor return for the time spent if you stop when you have explored only a single route to the answer. In typical cases, by spending twenty or thirty percent more time, you can study a few variations of the problem and for this slight extra time can learn two or three times as much. If your time is very short, instead of doing all the problems and then stopping, do three out of four, but review the three. During the review, light may dawn so that you can do the fourth problem in not much extra time. If you doubt that this extra study pays big dividends, just try it. I know it takes extra time in the short run, but there is no question about its paying off in the long run.
After two or three students have worked a set of problems independently, it is entirely in order, and quite worth while, for them to have a review session with each other concerning the problems. [12]
If you really understand the principles involved in problems, you will find that there are perhaps only half a dozen fundamental ideas presented in a whole week’s stint. Each principle may have a dozen variations. It is much wiser to go after the main idea than to try to memorize all the variations without correlating them to the main principle. For this reason, when you start working a problem don’t merely hunt in the text for some formula that may seem to have the right kinds of symbols in it. Your procedure should be to analyze the problem to see what physical principles are involved and then to work on that basis. The formulas are merely shorthand representations for the principles. Analyzing from principles rather than hunting for formulas may take a bit longer (especially the first time you try it) but you will learn more.
For example, the general problem of calculating potential energy, work, kinetic energy, etc., and of correlating these quantities with the distances the bodies move and with their velocities, etc., has so many variations that no student can hope to memorize them all. Yet dozens of variations of this general problem can be handled with the aid of a few physical principles which can be expressed mathematically in one or two square inches of notes. For this case these simple relations are: PE = mgh, KE = mv2/2 + Iw2/2, work = Fs cos(θ), and a statement of the principle of conservation of energy.
Be sure you know what the symbols stand for. because formulas without definitions mean nothing. (The student who hasn’t reached this point in his physics course may wonder what the symbols mean, but he will find out in due time.) For a whole week’s work you may need to memorize no more than the set of formulas just mentioned but the rest of the week’s work is to learn to apply them properly. Actually you may easily apply the right formula in the wrong way if you do not understand the fundamentals. Rely on your memory only for the few essential formulas and for the rest learn to reason from the fundamental principles.
As an example of proper procedure in working problems, consider the following question: If in the take-off of an airplane, a 192-pound man is uniformly accelerated for 16 seconds over a distance of 1280 feet, what force is exerted on him (by the seat)?
Step 1. Read the problem carefully.
Step 2. Reduce the problem to: A 192-pound object is accelerated from rest for 16 seconds over a distance of 1280 feet by what force?
Step 3. Since all the motion is in a straight line, a diagram is unnecessary.
Step 4.
Given:
Required:
Step 5. Relevant principles for uniformly accelerated motion starting from rest and for problems involving force and motion:
equation (1)
Perhaps in your course, equations (5) and (6) will be combined to give
equation (7)
In these equations, v = final velocity, a = acceleration, <v> = average velocity, m = mass, and g = the acceleration of gravity of 32 ft/sec2.
Step 6. To solve for the force from either equation (5) or (7), we must find the acceleration. The acceleration appears in equations (1), (3), and (4). Which one shall we choose? Since we do not know the final velocity v in equations (I) and (4), we must obtain the acceleration a from equation (3) in which we know both the distance s and the time t.
Step 7. From equation (3) we have
equation (8)
Now when the expression for a in equation (8) is substituted into equation (7) we get
equation (9)
W 2s
F = — ——
2
g t
Step 8. Putting in the numbers, we have
192 pounds 2x1280 ft 192 pounds 2x1280 ft
F = —————————— —————— —— = —————————— —————————
2 2 2 2 2 2
32 ft/sec 16 sec 32 ft/sec 16 sec
Step 9. Check the problem.
Step 10. Check the units. The units may be canceled as if they were fractional quantities, as shown. Every unit cancels except ‘pounds,’ which is a perfectly proper unit for force.
Step 11. Considering the way one sinks back in his seat on the take-off of a modern airliner, or even in an automobile starting in low gear, 60 pounds appears to be a reasonable accelerating force for a 192-pound man.
Step 12. The answer book gives 60 pounds for the answer.
Step 13. This is the all-important step—review the problem.
Working the problem backward involves solving: What time is required for a 60-pound force to accelerate a 192-pound object uniformly over a distance of 1280 feet? Or: What distance is required for a 60-pound force to accelerate a 192-pound object for 16 seconds? (You had better work out both problems just to make sure you are following along.) Variations of the problem include finding the average acceleration (for instance, from equation (8)—the answer is 10 ft/sec2), and the final take-off velocity (the answer is 160 ft/sec or about 109 miles/hour). Then you can work backward from the last two variations. If you keep this up, of course, it will take time, but as a studying system, this actually works. Some amount of time can be saved by omitting the numerical part of the review...
Many students, plagued by derivations, wonder why they must be studied. The chief reason is that many formulas are of limited validity because in the derivation some simplifying assumption is made that limits the generality. Thus if acceleration is assumed to be constant, one may use the formula that the distance a body moves from rest is given by (1/2) (acceleration) (time) 2. When the acceleration is not constant, however, this formula does not give the correct answer. For instance, in the case of simple periodic motion, where the acceleration is proportional to the displacement from the midpoint, another approach is needed. Frequently it is just as necessary to know the range of usefulness of a formula as it is to know the formula itself.
Another reason for studying derivations is that they often illustrate fundamental principles. Ten years ago students studying the diffraction pattern produced by an illuminated slit did not know that the same method of procedure would enable them to calculate the directional characteristics of an underwater sound signaling apparatus. Some of the students who had studied the principles, however, were able during the war to make useful contributions to the problem of locating enemy submarines. Students who had merely tried to memorize formulas could see no connection between the two kinds of phenomena, both of which involve wave motion (light waves and sound waves). Similar considerations apply to the directional characteristics of radar.
Another reason for studying derivations is that if you can derive a formula, you are not lost if you forget it during an exam, nor are you likely to use it in the wrong way.
Still another reason for studying a derivation springs from the fact that most of the technological information you have when you leave college gradually will become obsolete. If all you have learned in college is the end result, you, too, will become obsolete. If, however, you understand the intermediate steps, then as extensions are developed you will be able to fit them in with what you know.
A good way to discover why you don’t understand a derivation is to go back to the very beginning and go through it again carefully. One step missed somewhere can throw you completely off, and a review of the steps helps you to remember them as well as to understand them better. Do not expect that every mathematical relationship is an important formula. In the same way that many words are needed to build up to a concluding key sentence in a paragraph, often many mathematical equations are necessary to deduce some new principle from the initial assumptions. A whole page of math may be forbidding in its entirety but if you take it step by step, it may turn out to be fairly simple.
Probably you will need to memorize one or two dozen key formulas during your course. A convenient way to do this is to put the symbols of a given formula on one side of a 3×5 inch card, and on the other side to put the complete formula, the meaning of the symbols, the application of the formula to a typical problem, and suitable units. If on looking at the first side of the card you can’t give the information on the other side, you place the card back in your pile of formula cards near the top. If you know the material well, you place the card on the bottom. Whenever you have a few minutes you run through a part of or all of your pile of cards. (The same method with smaller cards, works well in learning a vocabulary in a foreign language.)
Just because you have used a formula correctly in part of a problem is no reason why the same formula may not be properly used again in another part of the same problem. For instance, Ohm’s law, potential difference = current × resistance, may be applied successively to several parts of a problem on electrical networks.
If you do not want to waste a lot of time doing arithmetic, learn to use a slide rule. Get a simple, inexpensive one at first (for about one dollar). After you have used it for a while, you can tell which of the more complicated slide rules with fancy scales will be useful to you. [14]
There are some parts of physics that are almost impossible to explain without using calculus. Usually most of these parts are omitted from all but the most substantial first-year courses. If they are not left out of your course and you have not had calculus, you need not necessarily be in despair. It may be quite possible to understand the physical ideas, even if you can’t do the mathematical manipulation. Probably you can understand the principle involved in finding the side of a cubical box having a volume of 120 cubic inches, although unless you are a very rare student you cannot take cube roots directly to find that the cube root of 120 is 4.932. (The answer seems reasonable, though, because you know the cube root of 125 is 5.)
Mathematics is one of the most important tools of the engineer-scientist. The more math you know and can use, the better off you are. Do not, however, use mathematics to sidestep the effort of clear thinking or writing; do not use mathematics to the extent that simple ideas are obscured by it. Do not get bogged down in the mathematics of a discussion. At all costs keep in mind the physical ideas.
An experiment is a controlled quantitative investigation—controlled in the sense that the various quantities entering into the experiment are under the control [16] of the experimenter and quantitative in the sense that numerical data are obtained. There is nothing mysterious about an experiment: the investigator ordinarily proceeds according to the scientific method.
There are several ways in which you may expect to benefit from the laboratory work. It helps you to understand and remember the physics you have studied; it gives you practice in the application of physical laws and logic to real cases, and in that way aids you to think clearly: and it gives you some skill in the use of scientific instruments and techniques.
A whole year’s course adds up to less than two full weeks of actual laboratory time (the Ph.D. candidate ordinarily spends about two years of full-time laboratory work on a single problem) so that you cannot expect to get any very thorough mastery of specialized laboratory techniques; however, you can learn much about less specialized techniques. You can try to get the most reliable data possible from first-year equipment that is often oversimplified and therefore not capable of high precision. In this way you will become familiar with averaging and estimating procedures as well as with experimental techniques for improving the accuracy of measurements in difficult situations where ideal measuring equipment has not yet been developed. Should you think of objecting to making several runs with the free-fall apparatus to improve the accuracy of your average value for the acceleration of gravity, remember that it may have taken many months to determine accurately a single figure for some quantity that appears in a handbook. It is true that you are not likely to be the discoverer of anything new in physics during your first-year course, for most (but not all) of the material in first-year physics has been known for decades. It is also true that you have not known the material for decades and you may, therefore, be able to experience the thrill in the laboratory of discovering for yourself some of the principles of physics. Most of the principles of physics were discovered by men using equipment no better than yours. Most of it, in fact. was not as good. At times, unfortunately, you will know beforehand what the results of your experiment are supposed to be, since mature investigators have done the experiment many times over. Even so, you can imagine yourself rediscovering the principles of physics while you are in the laboratory. With the equipment in front of you, you have the chance to try out your own ideas, to reason about the results, and to draw conclusions from them. In brief, you should regard the laboratory as a place for intellectual exploration .
Before you come to the laboratory, study the laboratory manual so that you will know what you are going to do and so that you can plan in advance how to use your time efficiently. As you do the experiment, make an effort to correlate the behavior of the apparatus with the principles discussed in lecture. To get an idea of the reliability of your measurements, after you have determined what you think is the best reading, gradually put the apparatus out of balance (or whatever is appropriate) to see how great an unbalance you can secure before the effect becomes noticeable. Make some record in your data of this observation. Pay special attention to the derivations and the equations used; eventually, when you substitute values into the equations, you will know why you use them.
Keep your mind open and alert to the possibilities of the experiment: try out things not specifically asked for in the instructions. True, your first original ideas may not seem particularly brilliant to you if the instructor points out their obvious fallacies but you must begin thinking for yourself sometime (rather than merely learning from a book) and the laboratory is a good place to start. The equipment is handy and the results of trying your own ideas are apparent immediately.
Constantly ask yourself such questions as: Why do we do it this way? What would happen if we did it another way? What does this measurement show or prove? The purpose of the laboratory manual is to direct your thinking along those channels most likely to be fruitful. Let us hope the manual is clear enough so that you need not waste time puzzling over simple matters. The manual, however, cannot possibly deal with all the points that can bc uncovered by a wide awake student. A few examples may be cited.
In the mechanics experiment on vectors using the force table the theory is straightforward and were it not for friction in the pulleys, the weight of the strings, and the weight of the ring, ‘perfect’ results could be anticipated. Discrepancies of a few percent are obtained ordinarily. The student who ‘takes’ physics will pass off the discrepancy vaguely as being due to some unspecified kind of friction, hurry through the experiment, and leaves the laboratory as soon as he can. The student who wants to make use of the opportunities to learn from the laboratory will devise procedures to diminish the errors or, if that is not possible, to correct for them. For instance, he may weigh the ring and the strings to estimate a limit for the error they introduce.
In the electricity experiment on divided circuits, the student can measure the current in some resistor both with and without the voltmeter being connected across it, thereby providing an estimate of the inaccuracy in the current reading introduced by the voltmeter (which takes some current). Likewise, he may measure the voltage with and without the ammeter in the circuit.
In the optics experiment on diverging lenses, the student may wish to apply the concave-mirror procedure to determine by reflection the radii of curvature of the lens, from which he can calculate the focal length if a value of the index of refraction of the glass is assumed. This focal length may be compared with the experimental value to serve as a check on the accuracy of the assumed index of refraction. Such measurements may not be suggested in the laboratory manual but alert students have thought of them and unquestionably did profit by making them.
A student must realize that the laboratory work has applications outside the laboratory. The centrifugal force experiment may suggest to the student that he calculate the force due to an unbalanced tire on an automobile traveling at high speed (e.g., assume two ounces unbalanced weight at the rim). The magnetometer experiment may suggest ideas in connection with the magnetic prospecting for minerals. The experiment on diffraction may help to explain why better directivity is obtained from the higher frequency radars. The experiment on optical instruments may suggest an approach to the projection of television pictures. There are, of course, innumerable other examples.
Writing laboratory reports is a significant part of your professional training. Speaking and writing are the most important tools of the engineer-scientist. Learn to handle them well. It takes work to transfer thoughts from your mind to somebody else’s. Your report should convey information to the reader rather than puzzle him. Anyone who has ever suspected that the author of a vague, verbose, confusing technical book seems to be trying to prevent overcrowding at the top by making it difficult for the uninformed, should recognize the importance of lucid expression. Your report should be well-organized, accurate, clear, concise, and easy to read. Since you will have to write reports anyway, while you’re doing them try to improve your command of the English language. Do not try to impress the reader with your own learning but write as if you were trying to explain the matter to an intelligent personal friend. Ability to express oneself clearly is extremely important for the professional man, even if a few people may tell you otherwise. Careful habits in handling things and in making accurate quantitative statements should encourage the professional man to an equal nicety in the use of words and to an observance of rules regarding their arrangement.
A few horrible examples will illustrate rome of the differences between bad and good English.
In answer to the question: “In the rifle-bullet ballistic-pendulum experiment, what principle determines the height to which the block will swing after it is struck by the bullet?” one student wrote: “The principal [sic] is that in the transfer of energy from one body to another, the total amount of the original body goes into the other body and the force which it has (the old body) will be related to the moment of inertia [sic] of the new body and the torque applied by the force of the old body. Therefore the block uses the distance which the force of the bullet can make the block go with the blocks [sic] inertia and mass as it is.” A better answer is: “The potential energy of the block (weight × height) at the top of the swing is equal to the kinetic energy of the block at the bottom of the swing just after impact.” [17]
An engineering report which read. “The optimum method of accomplishment of the purpose of the investigation...” was changed by an editor to “The best way of doing the experiment....”
In one of the professional journals, a ‘scholar’ wrote “Available evidence tends to indicate that it is not unreasonable to suppose that....” What he meant was, “Probably....”
Study these examples, laugh, and then take your work in English seriously. Be precise and concise; brevity is a virtue.
There is no particular objection to cramming except that most of it is a waste of time. Cramming a set of formulas into your head an hour before the exam may raise your score, and in that sense may be justified, or it may merely confuse you. Certainly you will not be able to learn any significant amount of new material by cramming. Do not make the blunder of trying to memorize the tough spots, for unless you understand the basic ideas, your half-memorized effort will do you no good either on the exam or later. Probably the exam will concern the part of your half-learned material that you didn’t understand. If you do not have time to study all the material, then discard what you think is least important and forget about it. Learn the rest of the subject well. You may or may not be able to bluff your way through an essay question in economics but definitely you cannot do it in a physics problem. Either you can reason how to do the problem or you can’t. Hence, if time is too short for you to learn all the course, learn part of it cold not just ‘sort of’.
You may infer possible types of questions from previously given exams or quizzes or from the kinds of problems in the problem sets. Referring to your own exams will help for the final exam.
During your study, try to anticipate exam questions and plan what your answers should be. If you have a sufficiently good grasp of the material to be able to make up possible questions and then solve them without your notes, you are practically assured of an A. It puts you on the ‘other side’ of learning when you try to make up questions, This is a very effective kind of study, for in order to devise good questions you must have studied hr the fundamental ideas.
Read the questions carefully: you don’t get credit for getting the right answer to a wrongly read problem or for a part you didn’t do because you overlooked it in the rush. Take it easy and don’t start using your pencil until you have thought out just how to begin. A common practice of physics professors is to gauge the time to allot to a problem by giving the students five times as long as it takes another professor to get the right answer, This means that it is mechanically possible for a student to make a perfect score by spending forty minutes thinking what to write and only ten minutes writing during a fifty-minute exam.
Don’t rush; haste is likely to induce slipshod thinking. Work at a convenient pace but without wasting time.
Don’t try to read a complicated or unnatural meaning into a simple question. If it is really vague, then ask the instructor what was intended (be diplomatic). In essay questions or derivations, write legibly. The readers give credit only for what they can read and they do not spend much time trying to decipher chicken tracks or the faint marks made with very hard pencils. Do not cramp your thinking by cramping your writing. Use plenty of space (paper is cheap) and write clearly, preferably in ink if you are used to writing with a pen.
Think about the questions; don’t worry about how you are doing. As one student says, “Heaven and Earth won’t come down if you miss a problem.” Don’t spend too long on any one question. Don’t hurry to do a lot of arithmetic until you are sure it is necessary (frequently things will cancel out if you give them a chance). Don’t work on scratch paper (you are certain not to get points for it). Do everything in an orderly fashion in your bluebook. Don’t take time to erase anything but rather cross it out neatly if it is wrong. Perhaps it is right after all, and you will get partial credit if you leave it in. (Decide which to do.) You are likely to get more partial credit for an incomplete answer if the arrangement of the material you do have is neat and orderly. Underline or box your final answers and remember to put down the units,
Ten minutes before the examination is over, take about one minute to check your work to make sure you have made no major blunder (such as leaving out an easy question) and to plan how you can use the remaining few minutes to the best advantage.
After the exam papers have been returned to you, be sure to clear up the points you missed: there is no need to lose credit on the final exam for the same mistakes. Furthermore, if you clear up weak points, it improves the solidarity of your foundation so that later material is learned more easily.[18]
Now you may say, “Yes, I agree with your ideas on how to study,” and then you may proceed to forget all about them. In that case, neither of us is better off than if you had never read this book. A good plan is to put this guide where you may review it occasionally. You will be interested to see how your own ideas change as you get further along. Ten years from now you will wish you had done things differently while you were in collage Probably most of the thoughts in here on what you should do in college would have come to you sooner or later anyway but it is my hope that from studying this manual you will get these thoughts soon enough for them to be helpful to you.
How many ideas in the Summary on the previous page can you give right now? Perhaps reading it again will be worth while, but before you reread it, see how much of it you can remember now.
2. This is the ‘Carnegie rule’ that a student should spend at least two hours of serious study for every hour spent in class. —DES §
3. Of course you must also know the details, but they won’t do you much good unless you see the whole picture. —DES §
4. There are over three dozen first-year physics texts on the market; clearly. Some must be better than others. First printings of first editions are more likely to have typographical errors than later printings. Chances are, however, that your text is at least 99 percent accurate. §
5. A good discussion is to be found in C. Gilbert Wrenn and Luella Cole: How to Read Rapidly and Well (Stanford University Press), 15 cents. §
6. The original document used the mathematical symbol for ‘therefore’ (a triangle of three dots). There is no HTML equivalent, so we use :. as a replacement. —DES §
7. A useful book is: Schaum, Outline of College Physics, with several hundred problems solved in detail with explanations, Schaum Publishing Company, $l.25. The “Schaum’s Outline Series” is now published by McGraw-Hill. —DES §
8. A very good booklet on mathematics problems is: Dadourian, How to Study; How to Solve, Addison-Wesley, 50 cents. §
9. Some students find it useful to close their eyes and meditate on the problem, undistracted by even their own notes. §
10. For instance, the problem may be: A man of given weight runs up a flight of stairs in a certain time; what horsepower does he develop in lifting his weight against the force of gravity? If your answer comes out 30 horsepower, it is obvious that you have made a mistake, For no man can develop 30 horsepower even for a short time. Probably you determined the number of foot pounds of work done by the man per minute and then divided by 550 foot pounds per second per horsepower, thereby getting a wholly unreasonable answer, sixty times too large. Learn to estimate answers approximately; it helps in checking the reasonableness of your work. §
11. A reader is one of those underpaid essential persons (usually a senior or graduate student) who reads and grades a portion of the hundreds of papers turned in every week by the students in a large class. §
12. Note the order of events: work the problems independently, then review in a group session. —DES §
13. For instance, Lapp, Knight, and Rietz, Review of Pre-College Mathematics (Scott, Foresman and Company), $1.00. Other excellent and useful books are: Swartz, Clifford, Used Math for the First Two Years of College Science, Prentice-Hall, 1973 (This has recently been reprinted by the American Institute of Physics). Dalven, Richard, Math for Physics, McGraw-Hill, 1989. Kruglak, Haym and John Moore, Basic mathematics for the Physical Sciences, McGraw-Hill, 1963. Marion and Davidson, Mathematical Preparation for General Physics, Saunders, 1972. Woodruff, Bobby J., Terms, Tables and Skills for the Physical Sciences, Silver Burdett, 1966. —DES §
14. The advice applies to your first electronic calculator as well. Buy one with trig functions and exponentials and at least one storage register. Do not let the calculator do your thinking for you, but check its results with pencil-and-paper. It’s so easy to slip a decimal or enter an exponent incorrectly. In slide-rule days, students made fewer blunders, for they had to supply the decimal point, or power of ten, themselves. Just this year (1995) the British Examinations Board ruled that calculators would no longer be allowed in its exams, for students use them as a crutch to avoid thinking. —DES §
15. Some parts of the introductory paragraphs to this chapter are from Seville Chapman, Laboratory Manual Engineering Physics, The National Press, Millbrae. California; by permission. §
16. In the torsion pendulum experiment, for instance, the diameter of the torsion wire, its length, the moment of inertia of the plate or disc, the amplitude of vibration, etc., are under the control of the experimenter, who may vary them at will. §
17. Students studying the ballistic pendulum experiment must be careful to distinguish between that part of the experiment in which momentum is conserved (the impact) and that part in which energy is conserved the swing). Energy and momentum, although related, are entirely different quantities. §
18. A classic book of useful advice for taking various kinds of exams is: Huff, Darrell, Score, the Strategy of Taking Tests, Ballantine, 1961. Huff is the author of another classic: How to Lie With Statistics, published by Norton, and now in its 45th printing. —DES §
This document scanned and edited for HTML by Donald E. Simanek:
dsimanek@eagle.lhup.eduSymbols used:
‘Single quotes’; “double quotes”; plus or minus: ±; centered dot: ·.
Multiplication: × ; vertical bar: | ; superscript1/2.
Footnote (dagger): †.
em-dash (long hyphen): —; ellipsis (three dots): …
If your browser doesn’t support such symbols, you may need to translate them.
HTML browsers have a limited character set. In this document the
Greek letter alpha has been replaced by beta (ß),
and lower case omega by w.
Subscripts are also a problem: FA is F-sub-A, etc.
— is the em-dash, also used for horizontal lines in fractions: ————.
(pi) represents the mathematical constant pi.
:. is ‘therefore’.
Cosmetic edits: Nov 19, 1996.
Return to Donald Simanek’s page.